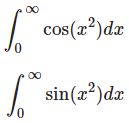tanのn乗根を定積分することを考える。cosとsinでは初等的には解けずガンマ関数を使わざるを得なかった。しかしtanのn乗根を積分すると初等的な形で意外ときれいな式が現れる。本記事ではまずは正攻法でゴリゴリと積分を試し、さらにベータ関数を用いた方法で導いていく。
定積分$$I_n\equiv\int_0^{\frac{\pi}{2}}\sqrt[n]{\tan x}dx \quad (n\ge 2)$$はいかなる値か．
について考察します( $n=1$ では発散するので除外)。
$\sin x$ や $\cos x$ の $n$ 乗根の積分については以前書きました。そのときはガンマ関数に帰着し、初等的に解けませんでした。
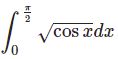$\int\sqrt{\cos x}dx$とガンマ関数・ベータ関数
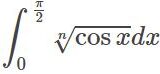$\int\sqrt[n]{\cos x}dx$ の計算 (ガンマ関数,ベータ関数)
これらはベータ関数との関係式$$B(x,y)=2\int_0^{\frac{\pi}{2}}\sin^{2x-1}\theta \cos^{2y-1}\theta d\theta \quad (x,y>0)$$およびガンマ関数に関する公式$$B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$を利用して求めたわけです。よって $\tan$ は $\cos$ と $\sin$ の組み合わせですから、同様にできると考えられます。しかしこれでは本記事が一瞬で終わってしまいますので、とりあえずまともに計算を試みます。
$n$ が小さいほど積分をしやすそうなので、まずは $n=2$ からです。$$I_2=\int_0^{\frac{\pi}{2}}\sqrt{\tan x}dx$$ $y\equiv \sqrt{\tan x}$ とおくと$$I_2=\int_0^\infty\frac{2y^2}{1+y^4}dy$$$y$ は $x$ に書き改めておきます。$$I_2=2\int_0^\infty\frac{2x^2}{1+x^4}dx$$$1+x^4=(x^2+\sqrt{2}x+1)(x^2-\sqrt{2}x+1)$ なので\begin{eqnarray*}I_2&=&\int_0^\infty \frac{1}{\sqrt{2}}\left(\frac{x}{x^2-\sqrt{2}x+1}-\frac{x}{x^2+\sqrt{2}x+1} \right)dx\\ &=& \int_0^\infty \frac{1}{2\sqrt{2}}\left(\frac{2x-\sqrt{2}}{x^2-\sqrt{2}x+1}+\frac{\sqrt{2}}{x^2-\sqrt{2}x+1}-\frac{2x+\sqrt{2}}{x^2+\sqrt{2}x+1}+\frac{\sqrt{2}}{x^2+\sqrt{2}x+1} \right)dx\\ &=& \frac{1}{2\sqrt{2}}\left[\log\frac{x^2-\sqrt{2}x+1}{x^2+\sqrt{2}x+1}\right]^\infty_0+\frac{1}{2}\int_0^\infty\left(\frac{1}{x^2-\sqrt{2}x+1}+\frac{1}{x^2+\sqrt{2}x+1}\right)dx\\ &=& \frac{1}{2}\int_0^\infty\left(\frac{1}{x^2-\sqrt{2}x+1}+\frac{1}{x^2+\sqrt{2}x+1}\right)dx\\ &=& \int_0^\infty\left(\frac{1}{1+(\sqrt{2}x-1)^2}+ \frac{1}{1+(\sqrt{2}x+1)^2}\right)dx\\ &=& \frac{1}{\sqrt{2}}\Bigl[\arctan(\sqrt{2}x-1)+\arctan(\sqrt{2}x+1)\Bigr]_0^\infty\\[1em] &\therefore& I_2= \frac{\pi}{\sqrt{2}}\end{eqnarray*}$\arctan$ なんて知らないよって場合は、第1項で $\sqrt{2}x-1=\tan\theta$ と置くなどすれば解けます。
$n=3$ でも同様に $y\equiv \sqrt[3]{\tan x}$ とおき、$y$ を $x$ に書き改めると\begin{eqnarray*}I_3&=&\int_0^\infty\frac{3x^3}{1+x^6}dx\\ &=& \int_0^\infty\left(\frac{x^3+x}{x^4-x^2+1}-\frac{x}{x^2+1}\right)dx\\ &=&\int_0^\infty\left(\frac{1}{4}\frac{4x^3-2x}{x^4-x^2+1}+\frac{3}{2}\frac{x}{x^4-x^2+1}-\frac{1}{2}\frac{2x}{x^2+1}\right)dx\\ &=& \left[\log\sqrt[4]{\frac{x^4-x^2+1}{(x^2+1)^2}}\right]^\infty_0+\int_0^\infty\frac{3}{2}\frac{x}{x^4-x^2+1}dx\\ &=& \int_0^\infty\frac{3}{2}\frac{x}{x^4-x^2+1}dx\\ &=& \frac{3}{2}\int_0^\infty\frac{xdx}{(x^2-\frac{1}{2})^2+\frac{3}{4}}\end{eqnarray*}$x^2-\frac{1}{2}=\frac{\sqrt{3}}{2}\tan\theta$ とおけば\begin{eqnarray*}I_3&=& \frac{\sqrt{3}}{2}\int_{-\frac{\pi}{6}}^\frac{\pi}{2}d\theta\\ &=& \frac{\pi}{\sqrt{3}}\end{eqnarray*}となります。$I_2$ と $I_3$ に共通するのは、$y\equiv \sqrt[n]{\tan x}$ とおき$$I_n=\int^\infty_0\frac{ny^n}{1+y^{2n}}dy$$としてゴリゴリと分数をさばいていくことで解けるということです。これを一般の $n$ で考えてみるのも面白そうですが、骨が折れそうです。
そこで冒頭で触れたベータ関数による方法を用います。
前提知識は３つです。
$$B(x,y)=2\int_0^{\frac{\pi}{2}}\sin^{2x-1}\theta \cos^{2y-1}\theta d\theta \quad (x,y>0)$$
$$B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$
$$\Gamma(s)\Gamma(1-s)=\frac{\pi}{\sin s\pi}$$
これらを用いて冒頭の積分を計算すると\begin{eqnarray*}I_n & = & \int_0^\frac{\pi}{2} \sqrt[n]{\tan x}dx\\ &=&\int_0^\frac{\pi}{2} \sin^{1/n}x\cos^{-1/n}xdx\\ &=& \frac{1}{2}B\left(\frac{n+1}{2n},\frac{n-1}{2n} \right)\\ &=& \frac{1}{2}\frac{\Gamma(\frac{n+1}{2n})\Gamma(\frac{n-1}{2n})}{\Gamma(1)}\\ &=& \frac{1}{2}\Gamma\left(\frac{n+1}{2n}\right)\Gamma\left(1-\frac{n+1}{2n}\right)\\ &=& \frac{\pi}{2\sin\frac{n+1}{2n}\pi}\end{eqnarray*}なんと予想以上に簡単な値となりました。$n=2,3$ を代入してみれば、上で苦労して求めた値がちゃんと出てきます。$n=4$ 以降はこれでさえややこしくなるので、やっぱり正攻法でまともにやる気にはなれませんね。
$$\int_0^{\frac{\pi}{2}}\sqrt[n]{\tan x}dx=\frac{\pi}{2\sin\frac{n+1}{2n}\pi} \quad (n\ge 2)$$
思ったよりきれいな結果になったのでいい気分です！
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
