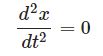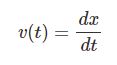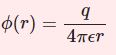屈折率が変化すると光は曲がる。本記事ではフェルマーの原理からはじめて屈折率と光の経路の関係を「変分法」の観点から考えていく。関数の最小値を求める微分とは違い、積分値（かかる時間）を最小にするような関数を求めることを変分法という。変分法は物理のさまざまな分野で応用されるため、学習は必須といってよい。
屈折率が変化すると光は曲がるというのは高校物理で学習することですが、屈折率と光の経路の関係を「変分法」の観点から考えてみたいと思います。
フェルマーの原理を起点とし、与えられた屈折率の分布から、変分法により光路を導く．
もくじ
フェルマーの原理とは、「光は光学的距離が最短になるような経路を進む」あるいは「最短時間で到達する経路を進む」というものです。この原理を認めることがスタートとなります。
手始めに高等学校の物理でも扱われる単純な屈折を考えます。光が屈折率 $n_1$ から $n_2$ の媒質へ入射し、入射角 $i$ 、屈折角 $r$ となったとします。さて $i , r$ にはいかなる関係があるでしょうか。
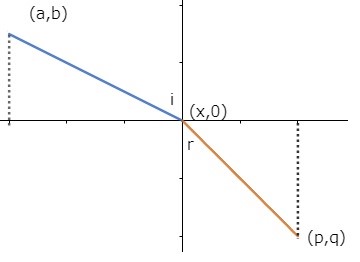
$(a,b)$ より光がやってきて、$x$ 軸上の点 $(x,0)$ で屈折し、その後 $(p,q)$ へ到達したとします。屈折率 $n$ における光の速さは $c/n$ であることに注意すれば、$(a,b)$ から $(p,q)$ へ至るのにかかる時間は$$T=\frac{n_1}{c}\sqrt{(x-a)^2+b^2}+\frac{n_2}{c}\sqrt{(p-x)^2+q^2}$$定数 $c$ をかけて$$cT=n_1\sqrt{(x-a)^2+b^2}+n_2\sqrt{(p-x)^2+q^2}$$ちなみに $cT$ を光学的距離といいます。最短時間つまり $T(cT)$ が最小になるには、微分して $0$ になることが必要ですから、$$\frac{d}{dx}(cT)=n_1\frac{(x-a)}{ \sqrt{(x-a)^2+b^2}}-n_2\frac{p-x}{\sqrt{(p-x)^2+q^2}}=0$$
三角比を用いれば$$\frac{(x-a)}{ \sqrt{(x-a)^2+b^2}}=\sin i\; ,\;\frac{p-x}{\sqrt{(p-x)^2+q^2}}=\sin r$$
と分かりますので結局$$n_1\sin i-n_2\sin r=0\Longrightarrow \frac{n_1}{n_2}=\frac{\sin r}{\sin i}$$のようにスネルの法則が求まります。
上で見た過程は、微分によって最短の光学的距離を求め、そうして出てきた経路が実現するよというわけです。では媒質の屈折率が連続的変化するときはどうすればいいでしょうか？
光は $xy$ 平面上を運動するとします。屈折率は場所によって変化するため $n(x,y)$ と表せます。光が点 $(x,y)$にいるときの速さは $c/n(x,y)$ ですから、距離 $\sqrt{dx^2+dy^2}$ を進むのにかかる時間は$$dt=\frac{n(x,y)\sqrt{dx^2+dy^2}}{c}$$$c$ をかければ微小な光学的距離についての式$$cdt=n(x,y)\sqrt{dx^2+dy^2}$$を得ます。光が点PからQへ $T$ 秒かけて進んだときの光学的距離は、この微小時間や微小距離を全部あつめて線積分であらわされ、$$cT=\int_{P\to Q}n(x,y)ds$$ただし $ds$ は微小な線素の大きさで、$ds=\sqrt{dx^2+dy^2}$ です。この線積分を最小にするような $x,y$ の関係式が、実現する光の経路をあらわすことになります。
光の経路は $xy$ 平面上のグラフとなりますから $y=y(x)$ の形で書けるとします。すると$$ds=\sqrt{dx^2+dy^2}=\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx$$とできるので、線積分は単なる $x$ の積分になります。光の出発点の $x$ 座標を $a$ 、到着点のそれを $b$ とおくと、最小にしたい積分は$$I=\int_a^bn(x,y)\sqrt{1+(y')^2}dx$$であるということになります。
ここで難しいのは、求めるべきは「上記の積分値 $I$ を最小にするような $y(x)$ の形」であることです。「最小にする値」でなく「最小にする関数形」なのです。そこで使われる武器が変分法です。
ある関数 $y$ で $I$ が最小になったとします。この関数の形を$\delta y$ だけ微小に変化させ、$y+\delta y$ とします（$\delta y$ で1つの文字）。するとこのとき、$I$ の変化 $\delta I=0$ となります。
これは関数の最小値（極小値）を考えることと似ています。
- 関数：$y$ が最小となる点から $x$ を少し変化させても$dy=0$
- 今回：$I$ が最小となる関数形から $y(x)$ を少し変化させても $\delta I=0$
これを手掛かりに計算してみます。まず被積分関数において $y,y',x$ を独立変数とみて$$L(y,y',x)\equiv n(x,y)\sqrt{1+(y')^2}$$とおきます。すると\begin{eqnarray*}\delta I&=&\int_a^b L(y+\delta y,y'+\delta y',x) dx-\int_a^b L(y,y',x)dx \\&=& \int_a^b \Bigl[ \frac{\partial L}{\partial y}\delta y+ \frac{\partial L}{\partial y'}\delta y' \Bigr]dx\\&=& \int_a^b \frac{\partial L}{\partial y}\delta y dx+ \int_a^b \frac{\partial L}{\partial y'}\delta y'dx\\&=& \int_a^b \frac{\partial L}{\partial y}\delta y dx+ \Bigl[ \frac{\partial L}{\partial y'}\delta y\Bigr]^b_a-\int_a^b \frac{d}{dx}\left(\frac{\partial L}{\partial y'}\right)\delta y dx\end{eqnarray*} 光路の始点・終点を固定しておけば $\delta y(a)=\delta y(b)=0$ ですから\begin{eqnarray*}\delta I&=& \int_a^b \frac{\partial L}{\partial y}\delta y dx-\int_a^b \frac{d}{dx}\left(\frac{\partial L}{\partial y'}\right)\delta y dx \\&=& \int_a^b \left[ \frac{\partial L}{\partial y}- \frac{d}{dx}\left(\frac{\partial L}{\partial y'}\right)\right]\delta y dx\end{eqnarray*}$\delta y$ は小さい任意の関数ですので $\delta I=0$ を満たすなら$$ \frac{\partial L}{\partial y}= \frac{d}{dx}\left(\frac{\partial L}{\partial y'}\right) $$が成立します。これは $y(x),y'(x),x$ を含んだ $y(x)$ についての微分方程式であり、これを解けば光路が分かるのです。
$$L(y,y',x)\equiv n(x,y)\sqrt{1+(y')^2}$$ とおくと解くべき方程式は $$ \frac{\partial L}{\partial y}= \frac{d}{dx}\left(\frac{\partial L}{\partial y'}\right)\tag{1}$$
抽象的で分かりにくいと思うので例で実践しましょう。
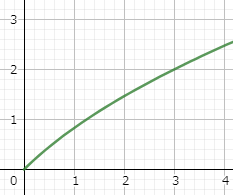
光が $(0,0)$ で入射し、入射したときの傾きが $y'(0)=1$ であったとする．屈折率が $n(x)=\sqrt{1+\displaystyle\frac{x}{2}}$ のとき光の経路を求めよ。
屈折率は $x$ 方向に増加していくので、経路の傾きはだんだん小さくなっていくことが予想されます。 $L(y,y',x)=n(x)\sqrt{1+(y')^2}$ は $y$ を変数にもっていないので(1)は$$\frac{d}{dx}\left( n(x)\frac{y'}{\sqrt{1+(y')^2}}\right)=0$$と書けます。従って定数を $C$ として$$n(x)\frac{y'}{\sqrt{1+(y')^2}}=C$$$n(0)=y'(0)=1$ なので $C=\frac{1}{\sqrt{2}}$ と求まり$$n(x)\frac{y'}{\sqrt{1+(y')^2}}=\frac{1}{\sqrt{2}}$$変形して$$2n(x)^2=\frac{1+y'^2}{y'^2}\Rightarrow x+2=1+\frac{1}{y'^2}$$よって$$y'(x)=\frac{1}{\sqrt{x+1}}$$積分して $y(0)=0$ を考慮すれば$$y(x)=2\sqrt{x+1}-2\;\;(x\ge0)$$これが求める経路になります。光の経路を図示したものが下図です。
光が $(0,0)$ で入射し、入射したときの傾きが $y'(0)=1$ であったとする．屈折率が $n(x)=x+1$ のとき光の経路を求めよ。
屈折率は $x$ 方向に増加していくので、経路の傾きはだんだん小さくなっていくことが予想されます。先の例題と同様の議論により$$y'=\frac{1}{\sqrt{2(x+1)^2-1}}$$積分して $y(0)=0$ を考慮すれば$$y(x)=\frac{1}{\sqrt{2}}(\mathrm{arccosh}\sqrt{2}(x+1)-\mathrm{arccosh}\sqrt{2})$$$\textrm{arccosh}$ は対数を使って書き直せます。$$y(x)=\frac{1}{\sqrt{2}}\log{(\sqrt{2}-1){\sqrt{2}(x+1)+\sqrt{2x^2+4x+1}}}$$これが求める経路となり、図示すると下図になります。
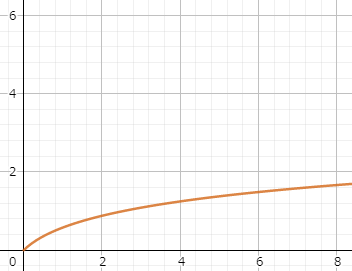
光が $(0,0)$ で入射し、入射したときの傾きが $y'(0)=1$ であったとする．屈折率が $n(y)=y+1$ のとき光の経路を求めよ。
$$L(y,y')=(y+1)\sqrt{1+(y')^2}$$ですので$$\frac{\partial L}{\partial y}=\sqrt{1+(y')^2}$$$$\frac{d}{dx}\left(\frac{\partial L}{\partial y'}\right)=\frac{y^{\prime\prime}(y+1)+y'^2}{\sqrt{1+y'^2}}-\frac{y'^2(y+1)y^{\prime\prime}}{(1+y'^2)^{3/2}}$$これらを等号で結び計算していくと$$y^{\prime\prime}(y+1)=1+y'^2$$なる微分方程式を得ます。
この微分方程式は非線型2階の方程式で、解くにはテクニックが要ります。$y$ を独立変数とみて $y'=u(y)$ とおきます。すると2階微分は$$y''=\frac{du(y)}{dx}=\frac{dy}{dx}\frac{du}{dy}=u\frac{du}{dy}$$微分方程式に代入して$$u\frac{du}{dy}(y+1)=1+u^2\Longrightarrow \frac{udu}{1+u^2}=\frac{dy}{y+1}$$変数分離ですね。両辺を積分して$$\log\sqrt{1+u^2}=\log(y+1)+C$$初期条件 $y(0)=0$ と $y'(0)=u(0)=1$ によって$$C=\frac{1}{2}\log2$$よって$$\log\sqrt{1+u^2}=\log\sqrt{2}(y+1)$$$u=y'$ に注意して変形をほどこすと$$\frac{dy}{dx}=\sqrt{2(y+1)^2-1} $$変数分離法によって$$\sqrt{2}x=\textrm{arccosh}\sqrt{2}(y+1)-\log(\sqrt{2}+1)$$移項して$$\textrm{arccosh}\sqrt{2}(y+1)=\sqrt{2}x+\log(\sqrt{2}+1)$$となり、$$\cosh(\sqrt{2}x+\log(\sqrt{2}+1))=\sqrt{2}(y+1)$$のように変形できます。最後は $\cosh$ の定義に従って計算して$$y(x)=\cosh\sqrt{2}x+\frac{1}{\sqrt{2}}\sinh\sqrt{2}x-1$$経路のグラフは下のようになります。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
