二重級数シリーズ第1回です。過去に多くの級数を計算してきました。収束性や順序交換等を深く考えず、いわば雑に二重級数を扱っていたのですが、そのあたりを丁寧に論じてみるのも、思ったより面白いです。
もくじ
$\epsilon$ 論法において、通常の数列と同様に定義します。
二重数列 $a_{mn}\in\CC$ が値 $a$ に収束するとは、次を意味する。$$\forall \epsilon>0,\;\exists N\in\NN,\;\forall m,n\ge N,\;|a_{mn}-a|<\epsilon$$このとき極限値を$$\lim_{m,n\to\infty}a_{mn}=a$$と書く。
$m,n$ について同時に極限をとるのであって、1つずつとるわけではありません。一般に定義1.1の極限と$$\lim_{m\to\infty}(\lim_{n\to\infty}a_{mn})$$は一致しません。これを逐次極限(repeated limitあるいはiterated limit)とよぶことにします。
$a_{mn}=\frac{1}{m}+\frac{1}{n}$ はゼロに収束することを示せ。また逐次極限も調べよ。
$N>2/\epsilon$ なる $N\in\NN$ をとると $\forall m,n\ge N$ に対して$$|a_{mn}-0|=\frac{1}{m}+\frac{1}{n}<\frac{2}{N}<\epsilon$$となり、示された。
なお、この数列については$$\lim_{m,n\to\infty}a_{mn}=\lim_{m\to\infty}(\lim_{n\to\infty}a_{mn})$$となっている。よって二重数列の極限と逐次極限は一致している。
$a_{mn}=(-1)^{m+n}\left(\frac{1}{m}+\frac{1}{n}\right)$ の収束性について、次を考察せよ。
(a) $\displaystyle\lim_{m,n\to\infty}a_{mn}$
(b) $\displaystyle\lim_{m\to\infty}(\lim_{n\to\infty}a_{mn})$
(a)は例1.2と同様の方法で $0$ である。(b)については $\displaystyle\lim_{n\to\infty}a_{mn}$ が発散(振動)してしまう。よって二重数列の極限と逐次極限は一致しない。
$a_{mn}=\frac{mn}{(m+n)^2}$ の収束性ついて、次を考察せよ。
(a) $\displaystyle\lim_{m,n\to\infty}a_{mn}$
(b) $\displaystyle\lim_{m\to\infty}(\lim_{n\to\infty}a_{mn})$
(b)は$$\lim_{m\to\infty}(\lim_{n\to\infty}a_{mn})=\lim_{m\to\infty}0=0$$となるので、逐次極限は $0$ である。しかし(a)のほうは $\forall N\in \NN$ , $m=N$ , $n=N$ ととると $a_{mn}\to \frac{1}{4}$ である。しかし $\forall N\in \NN$ , $m=2N$ , $n=N$ ととると $a_{mn}\to \frac{2}{9}$ である。よって $m,n\to\infty$ では収束しない。
(a)の発散を $\epsilon$ 論法でしっかり証明するなら、コーシー列でないことを示すといいでしょう(後述)。
以上のように、二重数列としての極限と逐次極限は異なることが多く、安易な操作には注意する必要があります。
二重数列 $\{a_{mn}\}$ の和を考えます。$m$ のみあるいは $n$ のみについて和をとるなら、それは普通の級数となります。$m,n$ ともに和をとる場合、二重級数となります。
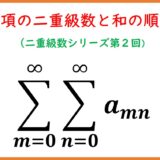
二重数列 $a_{mn}\in\CC$ による二重級数は$$\sum_{m=0}^\infty\sum_{n=0}^\infty a_{mn}=\lim_{m,n\to\infty}\sum_{i=0}^m\sum_{j=0}^n a_{ij}$$あるいは左辺を$$\sum_{m,n=0}^\infty a_{mn}$$とも書く。
こちらも $m,n$ 同時に極限をとっていることに注意します。一般に、これと逐次極限$$\sum_{m=0}^\infty\left(\sum_{n=0}^\infty a_{mn}\right)\;,\;\sum_{n=0}^\infty\left(\sum_{m=0}^\infty a_{mn}\right)$$は一致しません。というのも、定義1.2で $i=0~m$ , $j=0~n$ の部分和\begin{equation}S_{mn}:=\sum_{i=0}^m\sum_{j=0}^n a_{ij}\tag{1}\end{equation}を考えると、二重級数は\begin{equation}\sum_{m=0}^\infty\sum_{n=0}^\infty a_{mn}=\lim_{m,n\to\infty}S_{mn}\tag{2}\end{equation}であり、二重数列 $\{S_{mn}\}$ の極限といえます。よって前節の例などから一般に$$\lim_{m,n\to\infty}S_{mn}\;,\;\lim_{m\to\infty}(\lim_{n\to\infty}S_{mn})\;,\;\lim_{n\to\infty}(\lim_{m\to\infty}S_{mn})$$は一致せず、右2つをiterated seriesとよんでdouble seriesとは区別します。
もし二重級数が $S$ に収束する場合は定義1.1を $\{S_{mn}\}$ に適用します。そして$$\sum_{m,n=0}^\infty a_{mn}=\lim_{m,n\to\infty}S_{mn}=S$$と書きます。
通常の数列に比べて、和をとる順番をいろいろ考えることができます。
縦と横を順に足す(逐次極限)
二重数列は縦横に並べて書くことができます。\begin{equation}\begin{matrix}a_{0,0} & a_{0,1} & a_{0,2} &\cdots \\ a_{1,0} & a_{1,1} & a_{1,2} &\cdots\\ a_{2,0} & a_{2,1} & a_{2,2} &\cdots \\ \vdots &\vdots & \vdots& \end{matrix}\tag{3}\end{equation}(3)の「長方形」で和をとる場合、部分和は(1)と書けます。行ごと、列ごとに足すならばiterated seriesとなり、それぞれ\begin{eqnarray}\sum_{m=0}^\infty\left(\sum_{n=0}^\infty a_{mn}\right)=\lim_{m\to\infty}(\lim_{n\to\infty}S_{mn})=\lim_{m\to\infty}\left(\lim_{n\to\infty}\sum_{i=0}^m\sum_{j=0}^n a_{ij}\right)\tag{4a}\\\sum_{n=0}^\infty\left(\sum_{m=0}^\infty a_{mn}\right)=\lim_{n\to\infty}(\lim_{m\to\infty}S_{mn})=\lim_{n\to\infty}\left(\lim_{m\to\infty}\sum_{i=0}^m\sum_{j=0}^n a_{ij}\right)\tag{4b}\end{eqnarray}のように書き方にバリエーションがあります。先ほど述べたように、(4a)(4b)は逐次極限ですので、一般には二重級数の値とは一致しません。
正方形にとる
\begin{equation}\begin{matrix}a_{0,0} & & a_{0,1} & & a_{0,2}\\&&\downarrow&&\downarrow\\ a_{1,0} & \leftarrow& a_{1,1} & & a_{1,2}\\ & & & &\downarrow\\ a_{2,0} &\leftarrow & a_{2,1} &\leftarrow & a_{2,2}\end{matrix}\tag{5}\end{equation}のように項を並べます。すなわち \begin{equation}S_{mm}=a_{0,0}+(a_{0,1}+a_{1,1}+a_{1,0})+(a_{0,2}+a_{1,2}+a_{2,2}+a_{2,1}+a_{2,0})+\cdots\tag{6}\end{equation}群数列のようなイメージで、$m$ 群までとった部分和は $S_{mm}$ となります。ここでは「正方形並べ」とでもよびましょう。この極限は$$\lim_{m\to\infty}S_{mm}$$となります。
対角線にとる
\begin{equation}\begin{matrix}a_{0,0} & & a_{0,1} & & a_{0,2}\\&\swarrow&&\swarrow&\\ a_{1,0} & & a_{1,1} & & \\ & \swarrow& & &\\ a_{2,0} & & & & \end{matrix}\tag{7}\end{equation}のように和をとることを考えます。すなわち\begin{equation}\D_{m}=a_{0,0}+(a_{0,1}+a_{1,0})+(a_{0,2}+a_{1,1}+a_{2,0})+\cdots+(a_{0,m}+\cdots a_{m,0})\tag{8}\end{equation}と定義します。群数列のイメージをもたせて $m$ 群までとった部分和を $\D_m$ としました。これを「対角線並べ」とよびましょう。この極限は$$\lim_{m\to\infty}\D_{m}$$となります。
証明はしませんが、通常の級数と同様に次が成立します。
二重級数 $\sum a_{mn}$ , $\sum b_{mn}$ が収束すれば$$\sum(p a_{mn}+q b_{mn})=p\sum a_{mn}+q\sum b_{mn}$$
上で見たように、二重級数の部分和には様々な並べ方が考えられます。その並べ方によって極限は変わってしまうことがあります。以下の例を見てみましょう。
$$a_{mn}=\begin{cases}&1&\quad(m=n+1)\\&-1&\quad (m=n-1)\\&0&\quad(\mathrm{else})\end{cases}$$
(3)のように並べて書くと分かりやすい。\begin{equation}\begin{matrix}0 & -1 & 0 & 0 \\ 1 & 0 & -1 & 0\\ 0 & 1 & 0 &-1 \\ 0 & 0 & 1 & 0\end{matrix}\end{equation}2つの逐次極限は$$\sum_{m=0}^\infty\left(\sum_{n=0}^\infty a_{mn}\right)=-1\;,\;\sum_{n=0}^\infty\left(\sum_{m=0}^\infty a_{mn}\right)=1$$で異なっている。
正方形並べ(5)、対角線並べ(7)で足せば$$\lim_{m\to\infty}S_{mm}=0\;,\;\lim_{m\to\infty}\D_{m}=0$$となる。
また $\forall N$ に対して $m=n=N$ とした場合と $m=N+1,n=N$ とした場合では $S_{mn}$ の極限値が異なるため、二重級数は収束しない。
$$a_{mn}=\begin{cases}&(-1)^n&\quad(m=0\;,\; n>0)\\&(-1)^{m+1}&\quad (m>0\;,\; n=0)\\&0&\quad(\mathrm{else})\end{cases}$$
(3)のように並べて書くと分かりやすい。2つの逐次極限はともに発散するが、正方形並べと対角線並べではゼロに収束する。例4.1と同様に二重級数としては発散する。
$\sum_{n=0}^\infty b_n=0$ , $b_n\neq0$ を満たす $\{b_n\}$ がある。ここで二重数列$$a_{mn}:=(-1)^nb_m+(-1)^mb_n$$を定める。
\begin{eqnarray*}S_{mn} &=& \sum_{i=0}^m\sum_{j=0}^n\left[(-1)^jb_i+(-1)^ib_j\right] \\&=&\begin{cases}&\sum_{i=0}^m b_i+\sum_{j=0}^n b_j &\quad(m,n:\mathrm{even})\\&\sum_{j=0}^n b_j &\quad(m:\mathrm{even},n:\mathrm{odd})\\&\sum_{i=0}^m b_i &\quad(m:\mathrm{odd},n:\mathrm{even})\\& 0&\quad(m,n:\mathrm{odd})\end{cases}\end{eqnarray*}$b_n$ の条件から$$\lim_{m,n\to\infty}S_{mn}=0$$なので二重級数はゼロに収束する。ところが逐次極限では発散することがすぐに分かる。
通常の級数でコーシー列について解説しました。この二重数列バージョンを紹介します。
二重級数 $\sum a_{mn}$ が収束する必要十分条件は\begin{eqnarray}&&\forall\epsilon>0,\;\exists N\in\NN,\\ &&\quad\quad\forall p\ge \forall m\ge N,\;\forall q\ge \forall n\ge N,\;|S_{pq}-S_{mn}|<\epsilon\tag{*}\end{eqnarray}
【証明】(*)が成り立つとすると、特に $q\ge m$ としても成り立つので$$|S_{pp}-S_{mm}|<\epsilon$$とできる。よってコーシー列より $\{S_{mm}\}$ は収束して、先の $\epsilon$ に対して$$\exists N_1,\;\forall m\ge N_1,\;|S_{mm}-S|<\epsilon$$である。これにより $p\ge m\ge\max(N,N_1)$ かつ $q\ge m$ において\begin{eqnarray*}|S_{p,q}-S| &=& |S_{pq}-S_{mm}+S_{mm}-S|\\&\le&|S_{pq}-S_{mn}|+|S_{mm}-S|\\&<& 2\epsilon\end{eqnarray*}と書ける。よって $\{S_{mn}\}$ は収束する。
次に $\sum a_{mn}$ が収束するとすると、定義1.1を数列 $\{S_{mn}\}$ に適用すれば$$\forall \epsilon>0,\;\exists N\in\NN,\;\forall m,n\ge N,\;|S_{mn}-S|<\epsilon$$である。$p\ge m$, $q\ge n$ について$$|S_{pq}-S_{mn}|\ge|S_{pq}-S|+|S_{mn}-S|<2\epsilon$$であり、(*)を満たす。【証明終】
定理5.1は、収束すると予想されるが極限値が分からない、あるいは発散することを示す場合に有効です。次回以降も使いますので意識しておきたいです。
二重級数 $\sum a_{mn}$ が収束するならば二重数列としての極限は $\displaystyle\lim_{m,n\to\infty} a_{mn}=0$
【証明】定義1.1と仮定より $|S_{pq}-S_{mn}|<\epsilon$ である。$$a_{pq}=S_{p,q}-S_{p,q-1}-S_{p-1,q}+S_{p-1,q-1}$$より$$|a_{pq}|\le|S_{p,q}-S_{p,q-1}|+|S_{p-1,q}-S_{p-1,q-1}|<2\epsilon$$【証明終】
次回に続きます!
[1] Charles H.C.Little, Kee L.Teo, Bruce van Brunt, "An Introduction to Infinite Products" (2022) 楽天はココ。 [2] T.J.Bromwich, "An introduction to the theory of infinite series" (1908) [3] J.E.Brock, “An Example on Double Series.” The American Mathematical Monthly, vol. 50, no. 10, 1943, pp. 619–619.
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。