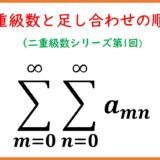
Frullani integral$$\int_0^\infty\frac{f(bx)-f(ax)}{x}dx=\bigl(f(\infty)-f(0)\bigr)\ln\frac{b}{a}$$およびその一般化$$\lim_{s\to +0}\int_0^\infty x^{s-1}\left\{f(ax)-g(bx)\right\}dx=\left\{f(0)-f(\infty)\right\}\left\{\ln\frac{b}{a}+\frac{d}{ds}\left.\left(\ln\frac{v(s)}{u(s)}\right)\right|_{s=0}\right\}$$を導出する。
もくじ
\begin{equation}\int_0^\infty\frac{f(bx)-f(ax)}{x}dx\quad(0<a<b)\tag{1.1}\end{equation}なる積分をFrullani integralといいます。ここで $f(x)$ は極限 $\displaystyle\lim_{x\to\infty} f(x)=f(\infty)$ をもち、$f(x)$ は微分可能で $f'(x)$ は連続と仮定します。
このとき\begin{eqnarray*}\int_0^R\frac{f(bx)-f(ax)}{x}dx &=& \int_0^R\left(\int_a^b f'(sx)ds\right)dx\\ &=& \int_a^b\left(\int_0^R f'(sx)dx\right)ds\\&=& \int_a^b\frac{f(sR)-f(0)}{s}ds\end{eqnarray*}$f'$ は連続関数なのでフビニの定理によって積分を交換しました。$f(sR)-f(0)$ は有界なので優収束定理から$$ \lim_{R\to\infty}\int_a^b\frac{f(sR)-f(0)}{s}ds=\int_a^b\frac{f(\infty)-f(0)}{s}ds$$したがって
\begin{equation}\int_0^\infty\frac{f(bx)-f(ax)}{x}dx=\bigl(f(\infty)-f(0)\bigr)\ln\frac{b}{a}\tag{1.2}\end{equation}
(1.2)を用いた例としては\begin{eqnarray}\int_0^\infty\frac{\arctan(bx)-\arctan(ax)}{x}dx &=& \frac{\pi}{2}\ln\frac{b}{a}\tag{2.1}\\\int_0^\infty\frac{e^{-bx}-e^{-ax}}{x}dx&=&\ln\frac{a}{b}\tag{2.2} \\\int_0^\infty\frac{e^{-bx^2}-e^{-ax^2}}{x}dx&=&\frac{1}{2}\ln\frac{a}{b}\tag{2.3}\end{eqnarray}
過去記事で紹介したように、ある条件を満たす(詳細は記事へ)関数 $\lambda(z)$ に対して
\begin{equation}\int_0^\infty x^{s-1}\sum_{n=0}^\infty \frac{\lambda(n)}{n!}(-x)^n dx=\G(s)\lambda(-s)\quad(0<s<1)\tag{3.1}\end{equation}
が成立し、Ramanujan's Master Theoremといいます。
"Ramanujan’s Notebooks Part I"のp314において、(3.1)による面白い公式の導出が書かれています。いま$$f(x)-f(\infty)=\sum_{n=0}^\infty\frac{u(n)(-x)^n}{n!}\;,\;g(x)-g(\infty)=\sum_{n=0}^\infty\frac{v(n)(-x)^n}{n!}$$なる展開式があるとし、$u(z),v(z)$ は(3.1)の $\lambda(z)$ が満たすべき条件を満足しているとしましょう。さらに\begin{equation}f(\infty)=g(\infty)\;,\;f(0)=g(0)\tag{4.1}\end{equation}と仮定し、次の積分を定めます。\begin{equation}I(s,a,b):=\int_0^\infty x^{s-1}\left\{f(ax)-g(bx)\right\}dx\tag{4.2}\end{equation}ただし $0<s<1$ かつ $a,b>0$ です。このとき $s\to0$ とすればFrullani積分(1.1)を一般化したものになることが分かります。計算すると\begin{eqnarray*}I(s,a,b) &=& \int_0^\infty x^{s-1}\left\{(f(ax)-f(\infty))-(g(bx)-g(\infty))\right\}dx \\&=& \int_0^\infty \left\{a^{-s}x^{s-1}(f(x)-f(\infty))-b^{-s}x^{s-1}(g(x)-g(\infty))\right\}dx\\&=& \int_0^\infty \left\{a^{-s}x^{s-1}\sum_{n=0}^\infty\frac{u(n)(-x)^n}{n!}-b^{-s}x^{s-1}\sum_{n=0}^\infty\frac{v(n)(-x)^n}{n!}\right\}dx\\&=&\G(s)\left\{a^{-s}u(-s)-b^{-s}v(-s)\right\}\quad(\because(3.1))\\&=&\G(s+1)\frac{a^{-s}u(-s)-b^{-s}v(-s)}{s}\\&=&\G(s+1)\frac{a^{-s}u(-s)-u(0)-b^{-s}v(-s)+v(0)}{s}\end{eqnarray*}ただし $u(0)=v(0)$ であることに注意。高等学校で習った微分の定義によって $s\to +0$ の極限をとると、\begin{equation}I(0,a,b)=v(0)\ln b-u(0)\ln a+v'(0)-u'(0)\tag{4.3}\end{equation}展開式から明らかに $u(0)=f(0)-f(\infty)$ , $v(0)=g(0)-g(\infty)$ で、(4.1)も用いて
\begin{equation}\lim_{s\to +0}\int_0^\infty x^{s-1}\left\{f(ax)-g(bx)\right\}dx=\left\{f(0)-f(\infty)\right\}\left\{\ln\frac{b}{a}+\frac{d}{ds}\left.\left(\ln\frac{v(s)}{u(s)}\right)\right|_{s=0}\right\}\tag{4.4}\end{equation}
$f(x)=g(x)$ とすると(1.2)と同じ式を得ますので、これはFrullani積分の一般化といえます。
例1
$p,q>0$ として $f(x)=(1+x)^{-p}$ , $g(x)=(1+x)^{-q}$ とすると $f(0)=g(0)=1$ , $f(\infty)=g(\infty)=0$ となります。このとき $f,g$ のマクローリン展開を考えると$$u(s)=\frac{\G(p+s)}{\G(p)}\;,\;v(s)=\frac{\G(q+s)}{\G(q)}$$となります。よって $a,b>0$ として(4.4)に適用すると
\begin{equation}\int_0^\infty\frac{(1+ax)^{-p}-(1+bx)^{-q}}{x}dx=\ln\frac{b}{a}+\psi(q)-\psi(p)\tag{5.1}\end{equation}
特に\begin{equation}\int_0^\infty\frac{(1+ax)^{-1/4}-(1+bx)^{-3/4}}{x}dx=\ln\frac{b}{a}+\pi\tag{5.2}\end{equation}とすると美しいです。
例2
こちらの「2023/5/29」より $q>0$ , $0<p<\frac{q}{2}$ に対して\begin{equation}\int_0^\infty x^{p-1}\left(\frac{2}{1+\sqrt{1+4x}}\right)^q dx=\frac{q\G(p)\G(q-2p)}{\G(q-p+1)}\tag{5.3}\end{equation}ところで、(3.1)で $\lambda(z)=\frac{q\G(q+2z)}{q+z+1}$ とおくと\begin{equation}\int_0^\infty x^{p-1}\sum_{n=0}^\infty \frac{q\G(q+2n)}{n!(q+n+1)}(-x)^ndx=\frac{q\G(p)\G(q-2p)}{\G(q-p+1)}\tag{5.4}\end{equation}(5.3)と(5.4)を比べて\begin{equation}\left(\frac{2}{1+\sqrt{1+4x}}\right)^q=q\sum_{n=0}^\infty\frac{\G(q+2n)}{n!\:\G(q+n+1)}(-x)^n\;,\;|x|\le\frac{1}{4}\;,\;q>0\tag{5.5}\end{equation}
さて $f(x)=(1+x)^{-p}$ , $g(x)=\left(\frac{2}{1+\sqrt{1+4x}}\right)^q$ とおきます。このとき $f(0)=g(0)=1$ , $f(\infty)=g(\infty)=0$ で、$$u(s)=\frac{\G(p+s)}{\G(p)}\;,\;v(s)=\frac{q\G(q+2s)}{\G(q+s+1)}$$となるので(4.4)に適用すると
\begin{equation}\int_0^\infty\frac{(1+ax)^{-p}-\left(\frac{2}{1+\sqrt{1+4bx}}\right)^q}{x}dx=\ln\frac{b}{a}+\psi(q)-\psi(p)-\frac{1}{q}\tag{5.6}\end{equation}
特に $p=q$ なら\begin{equation}\int_0^\infty\frac{(1+ax)^{-p}-\left(\frac{2}{1+\sqrt{1+4bx}}\right)^p}{x}dx=\ln\frac{b}{a}-\frac{1}{p}\tag{5.7}\end{equation}これはまたすごい式です。
例3
こちらの「2023/5/30」より $q>0$ , $0<p<q$ に対して\begin{equation}\int_0^\infty \frac{x^{p-1}dx}{(x+\sqrt{1+x^2})^q}=\frac{q\G(\frac{q-p}{2})\G(p)}{2^{p+1}\G(\frac{q+p}{2}+1)}\tag{5.8}\end{equation}例2と同様の手順で進めます。(3.1)で $\lambda(z)=\frac{2^{z-1}q\G(\frac{q+z}{2})}{\G(\frac{q-z}{2}+1)}$ とおいて(5.8)と比べることで\begin{equation}\left(x+\sqrt{1+x^2}\right)^{-q}=q\sum_{n=0}^\infty\frac{2^{n-1}\G(\frac{q+n}{2})}{n!\:\G(\frac{q-n}{2}+1)}(-x)^n\;,\;|x|\le1\tag{5.9}\end{equation}Berndt(1985)によれば(5.9)は $\forall q\in\CC$ で成立するようです。
さて $f(x)=(1+x)^{-p}$ , $g(x)=(x+\sqrt{1+x^2})^{-q}$ とおきます($p,q>0$)。このとき $f(0)=g(0)=1$ , $f(\infty)=g(\infty)=0$ で、$$u(s)=\frac{\G(p+s)}{\G(p)}\;,\;v(s)=\frac{2^{s-1}\G(\frac{q+s}{2})}{\G(\frac{q-s}{2}+1)}$$となるので(4.4)に適用すると
\begin{equation}\int_0^\infty\frac{(1+ax)^{-p}-(bx+\sqrt{1+b^2x^2})^{-q}}{x}dx=\ln\frac{2b}{a}+\psi(q/2)-\psi(p)+\frac{1}{q}\tag{5.10}\end{equation}
特に $q=2p$ なら\begin{equation}\int_0^\infty\frac{(1+ax)^{-p}-(bx+\sqrt{1+b^2x^2})^{-2p}}{x}dx=\ln\frac{2b}{a}+\frac{1}{2p}\tag{5.11}\end{equation}
証明と詳細については後日記載予定。Berndt(1985)のp317~318参照。
ある条件を満たす関数 $f(x)$ が関数 $u(s)$ を用いて\begin{equation}f(x)=\sum_{n=0}^\infty\frac{u(n)}{n!}(-z)^n\tag{6.1}\end{equation}と展開されているとします。$f(0)=0$ であるならば $u(s)$ は $s=0$ のまわりに展開できて微分可能であり\begin{equation}u'(0)=-\int_0^\infty\frac{f(x)}{x}dx\tag{6.2}\end{equation}となります。これをHafner's Lemmaとよびます。
例として $f(x)=\cos x-\frac{\sin x}{x}$ とします。明らかに $f(0)=0$ であり、$$f(x)=\sum_{n=0}^\infty\frac{2n}{(2n+1)!}(-1)^nx^{2n}$$(6.1)の形で書こうと思ったら $u(2n+1)=0$ , $u(2n)=\frac{2n}{2n+1}(-1)^n$ であってほしいです。これを満たす関数 $u$ は$$u(s)=\frac{s}{s+1}\cos\frac{\pi s}{2}$$微分係数は$$u'(0)=1$$ゆえに$$\int_0^\infty\left(\cos x-\frac{\sin x}{x}\right)\frac{dx}{x}=-1$$
数学の景色."Frullani integralとその証明" [2023/5/28アクセス]
あーるえぬ大学数学のあれこれ."ルベーグの収束定理を例題から理解する|証明・考え方を解説" [2023/5/28アクセス]
B.C.Berndt, "Ramanujan’s Notebooks Part I"(1985)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。