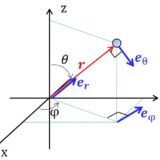
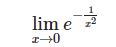とりあえず1つだけ.今後ネタを増やしていけたらと思います.
ベッセルの微分方程式や第1種ベッセル関数 $J_\nu(x)$ についてはたくさん過去記事があります.
積分表示については別の方法で導出した記事もあります.
$\nu=0$ としたベッセルの微分方程式\begin{equation}xy^{\prime\prime}+y'+xy=0\tag{1}\end{equation}から $J_0(x)$ の積分表示を導く.
この解 $y(x)$ をある関数 $f(z)$ とある経路 $C$ の逆ラプラス変換で表すと\begin{equation}y(x)=\int_Cf(z)e^{xz}dz\tag{2}\end{equation}$x$ で微分して$$y'(x)=\int_Czf(z)e^{xz}dz\;,\;y^{\prime\prime}=\int_Cz^2f(z)e^{xz}dz$$これを微分方程式(1)の左辺に代入します.$$xy^{\prime\prime}+y'+xy=\int_C(xz^2+z+x)f(z)e^{xz}dz$$
ここで$$(xz^2+z+x)f(z)e^{xz}=\frac{d}{dz}\left(e^{xz}g(z)\right)$$なる $g(z)$ を見つけます.右辺の微分を実行すると$$(xz^2+z+x)f(z)e^{xz}=\left[g'(z)+xg(z)\right]e^{xz}$$$$\therefore\;\left[(1+z^2)x+z\right]f(z)=g(z)x+g'(z)$$$x$ の係数を比べて$$\begin{cases}g(z)&=&(1+z^2)f(z)\\g'(z)&=&zf(z)\end{cases}$$辺辺割って積分すると$$g(z)=\sqrt{1+z^2}$$このとき$$f(z)=\frac{1}{\sqrt{1+z^2}}$$$$\therefore\;xy^{\prime\prime}+y'+xy=\int_C\frac{d}{dz}\left(e^{xz}\sqrt{1+z^2}\right)\cdot dz$$積分定数をゼロとしたので現れていませんが,実際は $g(z)$ , $f(z)$ には定数倍の不定性があります.これまでの議論により(1)を満たすには$$\int_C\frac{d}{dz}\left(e^{xz}\sqrt{1+z^2}\right)\cdot dz=0$$となればよいですね.
経路 $C$ の端点を $a,b$ とすると$$\int_C\frac{d}{dz}\left(e^{xz}\sqrt{1+z^2}\right)\cdot dz=\left[e^{xz}\sqrt{1+z^2}\right]_a^b$$ですので $a=-i$ , $b=i$ ととれば積分値はゼロとなります.
以上より微分方程式(1)を満たす $y(x)$ の積分表示は(2)より\begin{eqnarray*}y(x)&=&\int_Cf(z)e^{xz}dz\\&=&\int_{-i}^i\frac{e^{xz}}{\sqrt{1+z^2}}dz\\&=&\int_{-1}^1\frac{e^{ixt}}{\sqrt{1-t^2}}idt\\&=&i\int_0^1\frac{e^{ixt}}{\sqrt{1-t^2}}dt+i\int_0^1\frac{e^{-ixt}}{\sqrt{1-t^2}}dt\\&=&i\int_0^1\frac{e^{ixt}+e^{-ixt}}{\sqrt{1-t^2}}dt\\&=&2i\int_0^1\frac{\cos xt}{\sqrt{1-t^2}}dt\end{eqnarray*}と求まりました.
さて,(1)の特殊解は0次の第1種ベッセル関数 $J_0(x)$ です.この定数倍も解ですのでベッセル関数の積分表示$$J_0(x)=A\int_0^1\frac{\cos xt}{\sqrt{1-t^2}}dt$$を得ます.$J_0(0)=1$ であることを考慮すれば $A=2/\pi$ となるので
$$J_0(x)=\frac{2}{\pi}\int_0^1\frac{\cos xt}{\sqrt{1-t^2}}dt$$
エアリー方程式でもやってみました:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。