ルジャンドル関数の基礎２～第1種ルジャンドル関数の定義

前回はこちら：

ルジャンドル関数の基礎１～ルジャンドル多項式

第１種ルジャンドル関数の積分による定義

ルジャンドル多項式 $P_n(z)$ の $n$ を一般の複素数に拡張しましょう。こうしてできる関数を第1種ルジャンドル関数 $P_\nu(z)$ といいます。この定義にはいろいろな方法があるのですが、参考文献にしたがって美しい（？）もので進めていきます。

シュレーフリの積分表示

前回に見たシュレーフリの積分表示を再掲します。

定理０において $n$ を自然数に限定していますが、この式の雰囲気からすると、そもそも複素積分なのですから $n$ をより一般に拡張できそうな感じがします。

拡張の問題点

しかしながら $n$ が非整数の複素数の場合、定理０の周回積分は実はできず、定理０をそのまま使うことはできません。

どういうことかというと、経路を $z$ まわりを一周する小円だとします。一周させるとはすなわち $t-z=\epsilon e^{i\t}$ として $\t$ を $0$ から $2\pi$ に変化させることですが、$\t=0$ のときと $\t=2\pi$ のときでは、定理０の被積分関数の値は異なってしまいます（$e^{2\pi in}$ という余計なものが現れる。この現象は $n$ が整数のときは問題とならない）。これは $t=z$ が分岐点といわれるタイプの特異点であるためです。したがって定理０の周回積分では、1周した瞬間に被積分関数は不連続です。後述にて分かる通り、これが足かせとなってうまく拡張することができません。

分岐点問題の解消

そこで次のように定義しなおします。

なにやらややこしいですが、切断や分岐点の話は例えばこちらの例題を参照してください。あるいは当サイト等でキーワード検索してください。ともかく「$C$ は $1,z$ を時計回りに囲むが $-1$ は囲まない」のがポイントです。定義１において $\nu$ が整数ならふつうに留数計算をすればよいです（具体例は後述）。

今問題となっているのは $\nu\notin\ZZ$ の場合に生ずる分岐点です。$C$ を1周すると定義1の被積分関数において $t-1$ の偏角が $2\pi$ 増え、$t-z$ の偏角が $2\pi$ 増えます。$t=-1$ は囲まれていないので $t+1$ の最終的な偏角の変化はありません。すると$$\frac{(t+1)^\nu(t-1)^\nu}{(t-z)^{\nu+1}}\xrightarrow[]{\mathrm{add\:} 2\pi \:\mathrm{to}\:\arg}\frac{(t+1)^\nu(t-1)^\nu e^{2\pi i\nu}}{(t-z)^{\nu+1}e^{2\pi i(\nu+1)}}$$この両辺は一致しています。よって $C$ を1周すると被積分関数はもとの値に戻り周回積分ができることになります。これが重要なのです。

微分方程式の確認

定義１のように定めると $P_\nu(z)$ はルジャンドルの微分方程式\begin{equation}(1-z^2)y^{\prime\prime}-2zy'+\nu(\nu+1)y=0\tag{1}\end{equation}を満たすのです。それを確認しましょう。

$z$ での微分により\begin{align}P_\nu(z)&=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\\ P'_\nu(z) &=\frac{\nu+1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+2}}dt\\ P''_\nu(z) &=\frac{(\nu+1)(\nu+2)}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+3}}dt\end{align}となりますのでこれらを(1)の左辺に代入すると\begin{align}&(1-z^2)y^{\prime\prime}-2zy'+\nu(\nu+1)y\\&=\frac{\nu+1}{2^{\nu+1}\pi i}\oint_C\frac{(t^2-1)^\nu}{(t-z)^{\nu+3}}\left[(\nu+2)(1-z^2)-2z(t-z)+\nu(t-z)^2\right]dt\\&=\frac{\nu+1}{2^{\nu+1}\pi i}\oint_C\frac{d}{dt}\left[\frac{(t^2-1)^{\nu+1}}{(t-z)^{\nu+2}}\right]dt\\&=0\end{align}2番目のイコールについては、実際に微分してみると確かめられます。最後のイコールは先ほどと同様の議論で、$C$ を1周すると$$\frac{(t^2-1)^{\nu+1}}{(t-z)^{\nu+2}}$$は元の値に戻るためにゼロとなります。

以上から定義１で定められたルジャンドル関数は微分方程式(1)を満たします。さらに後述するように $P_\nu(1)=1$ が成立します。これらはルジャンドル多項式の基本的な性質でしたから、$P_\nu(z)$ はルジャンドル多項式の次数 $n$ を拡張したものになっています。

$P_\nu(z)$ の定義方法はほかにも超幾何級数による定義がありますが、$z$ の収束半径で制限がついてしまうなどを考えると、定義１が理論的には美しいといえると思います。ただし定義１そのままではあまりに一般化されすぎて、どんな値になるやらさっぱり見当がつかないという問題はあるでしょう。

ルジャンドル関数の具体的計算

そこで具体的に計算できるのかやってみます。

z=1の場合

$$P_\nu (1)=\frac{1}{2\pi i\cdot 2^\nu}\oint_C\frac{(t+1)^\nu}{t-1}dt$$$C$ は $1$ を囲みます。今の場合は $1$ は分岐点ではなく、ただの極です。よって留数定理により$$=\frac{1}{2\pi i\cdot 2^\nu} 2\pi i 2^\nu$$\begin{equation}\therefore\quad P_\nu (1)=1\tag{2}\end{equation}

z=-1の場合

$$P_\nu (-1)=\frac{1}{2\pi i\cdot 2^\nu}\oint_C\frac{(t-1)^\nu}{t+1}dt$$定義１を読むと $-1$ を囲むのか囲まないのか分かりませんが、いずれにせよ $\nu\notin\ZZ$ の場合は分岐点を生じて周回積分できません。

$z=-1$ かつ $\nu\in\ZZ$ のときも定義１には問題ありです。前回のルジャンドル多項式で得た値に合致させようとすると、$\nu$ が非負整数の場合は $-1$ を囲む、$\nu$ が負整数の場合は $-1$ を囲まないようにする必要があります。

しかしそのようなやりかたはご都合主義な感じなので、定義１は採用せず、前回みたルジャンドル多項式で成り立つ式 $P_n(-1)=(-1)^n$ およびいずれ紹介する $P_\nu(z)=P_{-\nu-1}(z)$ によって全整数へ拡張することができる、あるいは超幾何関数であらわすことで $z=-1$ でも定義できる（後述）ということで今は飲み込んでおきます。

νが非負整数

$\nu$ が整数の場合、定義１の積分は分岐点を生じません。特に非負整数の場合は $t=z$ にのみ $n+1$ 位の極をもち、定理０の式に一致します。留数定理により\begin{equation}P_n(z)=\frac{1}{2^nn!}\frac{d^n}{dz^n}(z^2-1)^n\quad(n\in\ZZ_{\ge 0})\tag{3}\end{equation}を得ます。前回紹介したロドリグの公式そのもので、ルジャンドル多項式と一致していることがわかります。

(3)を多項式の形で表すにはいくつか方法があります。今回は $z-1$ の多項式として表す方法を紹介します。簡単のためにポッホハマー記号 $(a)_n$ を用います。\begin{align}P_n(z) &= \frac{2^n}{n!}\frac{d^n}{dz^n}\left(\frac{z-1}{2}\right)^n\left(1+\frac{z-1}{2}\right)^n \\&= \frac{2^n}{n!}\frac{d^n}{dz^n}\sum_{r=0}^n\binom{n}{r}\left(\frac{z-1}{2}\right)^{n+r}\\ &=\sum_{r=0}^n\frac{(n+r)!}{r!^2(n-r)!}\left(\frac{z-1}{2}\right)^r \\&=\sum_{r=0}^n\frac{n!(n+1)_r}{r!^2(n-r)!}\left(\frac{z-1}{2}\right)^r\\&=\sum_{r=0}^n\frac{(n+1)_r(-n)_r}{r!^2}\left(\frac{1-z}{2}\right)^r\end{align}したがって超幾何級数の形をしており、\begin{equation}P_n(z)={}_2F_1\left[\begin{matrix}n+1 , -n\\ 1\end{matrix};\frac{1-z}{2}\right]\tag{4}\end{equation}と書けます。

超幾何級数なので普通は $|z-1|<2$ の制約がつきますが、今のケースでは級数が $r=n$ で打ち切られて多項式となっているので、$z$ は任意の複素数です。したがって $z=-1$ でも問題ありません。

νが負整数

のちに紹介するように、一般に $P_\nu(z)=P_{-\nu-1}(z)$ が成り立つので、$\nu$ が非負整数のルジャンドル関数を用いればすぐに解決します。ただし、今はまでそれを知らないものとしてまともにやってみましょう。

$n\in\NN$ とします。定義１は留数定理により$$P_{-n}(z)=\frac{2^n}{(n-1)!}\lim_{t\to 1}\frac{d^{n-1}}{dt^{n-1}}\frac{(t-z)^{n-1}}{(t+1)^n}$$関数の積に関するライプニッツの法則を用いて$$=\frac{2^n}{(n-1)!}\lim_{t\to 1}\sum_{r=0}^{n-1}\binom{n-1}{r}\left(\frac{d^r}{dt^r}(1+t)^{-n}\right)\left(\frac{d^{n-1-r}}{dt^{n-1-r}}(t-z)^{n-1}\right)$$２つの微分を実行して $t\to 1$ として計算を進めると$$=\sum_{r=0}^{n-1}\binom{n-1}{r}(-1)^r\frac{(n)_r}{r!}\left(\frac{1-z}{2}\right)^r$$さらに整理して$$P_{-n}(z)=\sum_{r=0}^n\frac{(1-n)_r(n)_r}{r!^2}\left(\frac{1-z}{2}\right)^r$$したがって超幾何級数の形で\begin{equation}P_{-n}(z)={}_2F_1\left[\begin{matrix}1-n , n\\ 1\end{matrix};\frac{1-z}{2}\right]\tag{5}\end{equation}

(4)(5)は全く同じなので、全整数で次がいえます。

定理２はルジャンドル多項式を $z-1$ で展開したものです。一方 $z$ で展開したものについては前回をご覧ください。

νが非整数

いよいよ厄介なところです。$\nu\notin\ZZ$ の場合、定義１$$P_\nu(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\quad(\nu\in\CC\;,\, z\neq -1)$$をどう計算するのか。いま$$f(t):=\frac{(t^2-1)^\nu}{(t-z)^{\nu+1}}=\frac{(t+1)^\nu(t-1)^\nu}{(t-z)^{\nu+1}}$$とおきます。$z$ は一般の複素数ですが、積分路を分かりやすくするため、ここでは実数 $x\in (-1,1)$ に限定します。積分路 $C$ を次のようにとります。

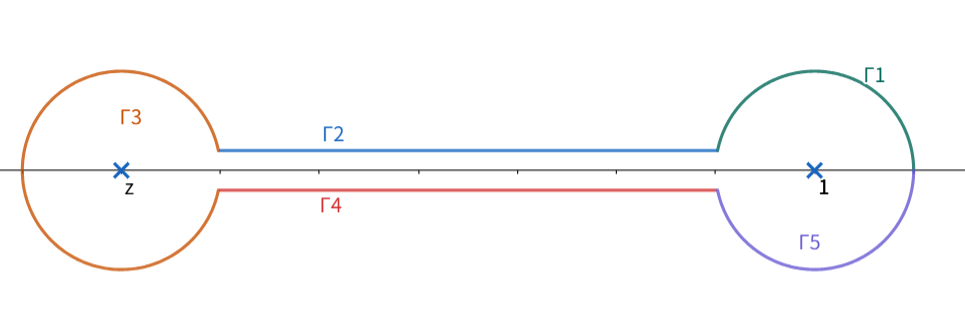
図より$$\oint_C=\int_{\G_1}+\int_{\G_2}+\int_{\G_3}+\int_{\G_4}+\int_{\G_5}$$$f(t)$ に関する偏角を$$0<\arg(t-1)<2\pi\;,\; 0<\arg(t-x)<2\pi$$に限定します。また経路は十分小さい円と実軸に十分小さい直線から成るため、常に $\arg(t+1)=0$ としてよいです。積分路のスタートは $t=1+\epsilon$ で $\arg(t-1)=0$ , $\arg(t-x)=0$ とします。ゴールはもちろん同一地点ですが偏角が $\arg(t-1)=2\pi$ , $\arg(t-x)=2\pi$ となります。

$\G_1$ では $t-1=\epsilon e^{i\t}$ とおいて $\t$ を $0$ から $\pi$ まで変化させます。$\arg(t-x)=0$ なので $t-x=1-x$、$\arg(t+1)=0$ なので $t+1=2$ です。$$\int_{\G_1}\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dz=\int_0^\pi \frac{2^\nu \epsilon^\nu e^{i\nu\t}}{(1-x)^{\nu+1}}i\epsilon e^{i\t}d\t$$\begin{equation}\therefore\quad\int_{\G_1}\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dt=-\frac{2^{\nu}\epsilon^{\nu+1}(1+e^{i\pi\nu})}{(\nu+1)(1-x)^{\nu+1}}\tag{6}\end{equation}

$\G_2$ では $\arg(t-1)=\pi$ なので $t-1=(1-t)e^{\pi i}$ です。$\arg(t-x)=0$ なので $t-x$ はそのまま $t-x$ と書き、$\arg(t+1)=0$ なので $t+1$ もそのまま $t+1$ と書きます。すると\begin{equation}\int_{\G_2}\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dt=e^{\pi i\nu}\int_{1-\epsilon}^{x+\epsilon}\frac{(1-t^2)^\nu}{(t-x)^{\nu+1}}dt\tag{7}\end{equation}

$\G_3$ では $t-1=(1-x)e^{\pi i}$ , $t+1=x+1$ , $t-x=\epsilon e^{i\t}$ として $\t$ を $0$ から $2\pi$ へ変化させます。すると\begin{equation}\int_{\G_3}\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dt=(e^{\pi i\nu}-e^{-\pi i\nu})\frac{(1-x^2)^\nu}{\nu\epsilon^\nu}\tag{8}\end{equation}

$\G_4$ では $t-1=(1-t)e^{\pi i}$ , $t-x=(t-x)e^{2\pi i}$ として\begin{equation}\int_{\G_4}\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dt=e^{-\pi i\nu}\int^{1-\epsilon}_{x+\epsilon}\frac{(1-t^2)^\nu}{(t-x)^{\nu+1}}dt\tag{9}\end{equation}

$\G_5$ では $t-1=\epsilon e^{i\t}$ とおいて $\t$ を $\pi$ から $2\pi$ まで変化させます。$t-x=(1-x)e^{2\pi i}$ , $t+1=2$ なので\begin{equation}\therefore\quad\int_{\G_5}\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dt=\frac{2^{\nu}\epsilon^{\nu+1}(1+e^{-i\pi\nu})}{(\nu+1)(1-x)^{\nu+1}}\tag{10}\end{equation}

(6)～(10)までを足して\begin{align}&\oint_C\frac{(t^2-1)^\nu}{(t-x)^{\nu+1}}dt\\&=(e^{\pi i\nu}-e^{-\pi i\nu})\left[\frac{(1-x^2)^\nu}{\nu\epsilon^\nu}-\frac{2^{\nu}\epsilon^{\nu+1}}{(\nu+1)(1-x)^{\nu+1}}-\int^{1-\epsilon}_{x+\epsilon}\frac{(1-t^2)^\nu}{(t-x)^{\nu+1}}dt\right]\tag{11}\end{align}

以上から

$\nu=-1/2$ の場合、$\epsilon \to 0$ として$$P_{-1/2}(x)=\frac{\sqrt{2}}{\pi}\int_x^1\frac{dt}{\sqrt{(1-t^2)(t-x)}}$$楕円積分の形をしています。$u^2=\frac{1-t}{1-x}$ の置換によって

次回へ続く。

参考文献

[1] Whittaker, E. T., & Watson, G. N. (2021). A course of modern analysis. Cambridge University Press.

第５版です。いわずと知れた名著。

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。