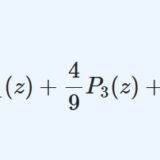前回は:
今回も第1種ルジャンドル関数のお話です。
以下の2つのテーマを扱います。互いに独立したテーマとなっているように見えますが、ルジャンドル関数の定義内にある積分経路をどのように設定するかがキモであるという点は共通しています。
$|1-z|<2$ , $\nu\in\CC$ , $$P_\nu(z)=F\left[\begin{matrix}-\nu , \nu+1\\1\end{matrix};\frac{1-z}{2}\right]$$
$\mathfrak{R}z>0$ , $\nu\in\CC$ , $$P_\nu(z)=\frac{1}{\pi}\int_0^\pi\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu d\phi$$ただし $(z^2-1)^{1/2}$ の枝は任意にとってよく、$[z+(z^2-1)^{1/2}\cos\phi]^\nu$ の枝は $\phi=\frac{\pi}{2}$ のときに $z^\nu$ と偏角が一致するようにとる。
両テーマとも、$\nu$ を整数に限った解説はよく見かけるのですが、ここでは複素解析を用いて $\nu$ が任意の複素数の場合でもカバーできるようにします。
まず第1種ルジャンドル関数の定義を思い出しましょう:
第1種ルジャンドル関数を次で定義する。$$P_\nu(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\quad(\nu\in\CC\;,\, z\neq -1)$$ただし経路 $C$ は $1,z$ を時計回りに囲むが $-1$ は囲まない.
$\nu$ が非整数の場合、$t$ 平面には $1$ と $z$ を結ぶ切断、$-1$ と $-\infty$ を結ぶ切断を入れる.
本節では $|1-z|<2$ という条件をつけます。$z$ の範囲は、$1$ を中心とする半径 $2$ の円の内部というわけです。
これを満たす $z$ を決めてやると、$0<\delta<1$ なる $\delta$ がとれて $$|1-z|\le 2(1-\d)$$とできます。
さて、定義0における積分経路 $C$ は定義0に書かれてある条件を満たしていれば、様々な形状にすることができます。ここでは $C$ を $|1-t|=2-\d$ なる円に設定します。すると $C$ は $1,z$ を囲み、$-1$ を囲まない円になっています。つまり定義0の条件を満たしています。
ここで$$t-z=(t-1)\left(1-\frac{z-1}{t-1}\right)$$であることから$$(t-z)^{-\nu-1}=(t-1)^{-\nu-1}\left(1-\frac{z-1}{t-1}\right)^{-\nu-1}$$と書けますが、$C$ 上で\begin{equation}\left|\frac{1-z}{1-t}\right|\le\frac{2-2\d}{2-\d}<1\tag{1}\end{equation}より、一様収束する次の二項級数で表されます。\begin{equation}(t-z)^{-\nu-1}=(t-1)^{-\nu-1}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}\left(\frac{z-1}{t-1}\right)^n\tag{2}\end{equation}
$(x)_n$ はポッホハマー記号といい、$$(x)_n=x(x+1)(x+2)\cdots(x+n-1)$$のように $x$ から1ずつ増やして $n$ 個の積をとるものです。
(2)式の右辺には関数項級数がありますが、これの一様収束性はワイエルシュトラスのM判定法とダランベールの収束判定法によって示せます。まず$$\sum_{n=0}^\infty\left|\frac{(\nu+1)_n}{n!}\left(\frac{z-1}{t-1}\right)^n\right|=\sum_{n=0}^\infty\frac{|(\nu+1)_n|}{n!}\left|\frac{z-1}{t-1}\right|^n$$(1)より$$\sum_{n=0}^\infty\left|\frac{(\nu+1)_n}{n!}\left(\frac{z-1}{t-1}\right)^n\right|\le\sum_{n=0}^\infty\frac{|(\nu+1)_n|}{n!}\left(\frac{2-2\d}{2-\d}\right)^n$$この右辺はダランベールの判定法で収束すると分かります。なぜなら$$\lim_{n\to\infty}\frac{a_{n+1}}{a_n}=\lim_{n\to\infty}\left|1+\frac{\nu}{n+1}\right|\left(\frac{2-2\d}{2-\d}\right)=\frac{2-2\d}{2-\d}<1$$したがってワイエルシュトラスのM判定法によりもとの関数項級数は一様収束(かつ絶対収束)であることが分かります。
では(2)を定義0に適用します。$$P_\nu(z)=\frac{1}{2^{\nu+1}\pi i}\oint_C(t^2-1)^\nu(t-1)^{-\nu-1}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}\left(\frac{z-1}{t-1}\right)^ndt$$少し整理して$$P_\nu(z)=\frac{1}{2^{\nu+1}\pi i}\oint_C\frac{(t+1)^\nu}{t-1}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}\left(\frac{z-1}{t-1}\right)^ndt$$級数が一様収束することから項別積分可能ですので、積分と総和の記号を入れ替えて$$P_\nu(z)=\frac{1}{2^{\nu+1}\pi i}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}\oint_C\frac{(t+1)^\nu}{t-1}\left(\frac{z-1}{t-1}\right)^ndt$$少し整理します。\begin{equation}P_\nu(z)=\frac{1}{2^{\nu+1}\pi i}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}(z-1)^n\oint_C\frac{(t+1)^\nu}{(t-1)^{n+1}}dt\tag{3}\end{equation}(3)の周回積分の計算は留数定理によります。 $t=1$ に $n+1$ 位の極をもつので\begin{equation}P_\nu(z)=\frac{1}{2^{\nu+1}\pi i}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}(z-1)^n\cdot\frac{2\pi i}{n!}\lim_{t\to 1}\frac{d^n}{dt^n}(t+1)^\nu\tag{4}\end{equation}ここで$$\frac{d^n}{dt^n}(t+1)^\nu=\nu(\nu-1)\cdots(\nu-n+1)(t+1)^{\nu-n}$$なので(4)は\begin{equation}P_\nu(z)=\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!^2}\left(\frac{z-1}{2}\right)^n\nu(\nu-1)\cdots(\nu-n+1)\tag{5}\end{equation}と書けますが、さらに$$\nu(\nu-1)\cdots(\nu-n+1)=(-1)^n(-\nu)_n$$を用いると\begin{equation}P_\nu(z)=\sum_{n=0}^\infty\frac{(-\nu)_n(\nu+1)_n}{n!^2}\left(\frac{1-z}{2}\right)^n\tag{6}\end{equation}と超幾何関数の形で書けます。これをMurphyの公式といいます。(6)を見ればわかるように、$\nu$ が整数であれば級数は途中で打ち切られて多項式になります。
$|1-z|<2$ , $\nu\in\CC$ , $$P_\nu(z)=F\left[\begin{matrix}-\nu , \nu+1\\1\end{matrix};\frac{1-z}{2}\right]$$
$\nu\in\CC$, $m\in\ZZ_{\ge 0}$ のとき$$\left.\frac{d^{m+1}}{dz^{m+1}}P_{m+\nu}(z)\right|_{z=1}=\frac{\G(\nu+2m+2)}{2^{m+1}(m+1)!\G(\nu)}$$
【解答】微分を実行すると定理1より$$\left.\frac{d^{m+1}}{dz^{m+1}}P_{m+\nu}(z)\right|_{z=1}=\left.\sum_{n=m+1}^\infty\frac{(-\nu-m)_n(\nu+m+1)_n}{n!(n-m-1)!}\left(-\frac{1}{2}\right)^{m+1}\left(\frac{1-z}{2}\right)^{n-m-1}\right|_{z=1}$$右辺は $z=1$ により $n=m+1$ 以外でゼロであることから$$=\frac{(-\nu-m)_{m+1}(\nu+m+1)_{m+1}}{(m+1)!}\left(-\frac{1}{2}\right)^{m+1}$$これを変形して答えを得る。
次のテーマに移ります。はじめに $\nu$ を自然数に限定したバージョンを解説します。
$\nu=n\in\NN$ の場合、定義0から$$P_n(z)=\frac{1}{2^{n+1}\pi i}\oint_C\frac{(t^2-1)^n}{(t-z)^{n+1}}dt$$定義0では $C$ は $1,z$ を囲み $-1$ を囲まないという条件をつけているのですが、今の場合は被積分関数の特異点が $t=z$ のみなので、$C$ は $z$ さえ囲んでおけばよくて、$1$ や $-1$ を囲もうが囲まないが問題ありません。
いま $C$ を $z$ 中心で半径 $|z^2-1|^{1/2}$ の円だとしましょう。$z=\pm1$ であれば半径がゼロになるので除外せねばなりません。値としてはルジャンドル多項式でみたように $P_n(1)=1$ , $P_n(-1)=(-1)^n$ となります。以下 $z\neq\pm1$ としましょう。
すると $C$ を一周するということは$$t=z+(z^2-1)^{1/2}e^{i\phi}$$とおいて $\phi$ を $-\pi$ から $\pi$ まで変化させることになります。
この置換を実行して$$P_n(z)=\frac{1}{2^{n+1}\pi i}\int_{-\pi}^{\pi}\frac{\left(z-1+(z^2-1)^{1/2}e^{i\phi}\right)^n\left(z+1+(z^2-1)^{1/2}e^{i\phi}\right)^n}{(z^2-1)^\frac{n+1}{2} e^{i\phi(n+1)}}(z^2-1)^{1/2}ie^{i\phi}d\phi$$少し整理すると$$P_n(z)=\frac{1}{2^{n+1}\pi}\int_{-\pi}^{\pi}\left[\frac{\left(z-1+(z^2-1)^{1/2}e^{i\phi}\right)\left(z+1+(z^2-1)^{1/2}e^{i\phi}\right)}{(z^2-1)^{1/2} e^{i\phi}}\right]^nd\phi$$分子を展開すれば$$P_n(z)=\frac{1}{2^{n+1}\pi}\int_{-\pi}^{\pi}\left[2z+(z^2-1)^{1/2}(e^{i\phi}+e^{-i\phi})\right]^nd\phi$$指数関数の部分は $\cos$ の形になっていますので$$P_n(z)=\frac{1}{2\pi}\int_{-\pi}^{\pi}\left[z+(z^2-1)^{1/2}\cos\phi\right]^nd\phi$$偶関数なので
\begin{equation}P_n(z)=\frac{1}{\pi}\int_0^{\pi}\left[z+(z^2-1)^{1/2}\cos\phi\right]^nd\phi\tag{7}\end{equation}ただし $(z^2-1)^{1/2}$ の枝は任意にとってよい。
定理2は $z=\pm1$ でも成立します。なお $\phi\to\pi -\phi$ なる置換によって(7)は\begin{equation}P_n(z)=\frac{1}{\pi}\int_0^{\pi}\left[z-(z^2-1)^{1/2}\cos\phi\right]^nd\phi\tag{8}\end{equation}とも書けます。
定理2に付した但し書きについて補足します。1/2乗というのは2価関数です。というのも例えば $z=2$ なら $(z^2-1)^{1/2}=\pm\sqrt{3}$ です。このように2つの値が出てきてしまい、$P_n(z)$ が2つの値をもってしまうように見えます。この問題を解消するために、一般的には正負のどちらをとるのか(どの枝をとるのか)を、両辺の値の整合性がとれるように指定するのです。しかし(7)と(8)を見れば符号の正負はいずれでもよく、1/2乗で生じる2価性が問題にならないのです。要は平方根の符号はどっちをとってもいいってことです。
では $\nu\in\CC$ へ拡張しましょう。定義0の積分を再掲すると$$P_\nu(z)=\frac{1}{2^{\nu+1}\pi i}\oint_C\frac{(t^2-1)^\nu}{(t-z)^{\nu+1}}dt\quad(\nu\in\CC\;,\, z\neq -1)$$で、$C$ は $1,z$ を囲み、$-1$ を囲まないのでした。
定理2の拡張をしたいので、先ほどと同様の置換積分を行うことになります。つまり周回経路 $C$ を $z$ を中心に半径 $|z^2-1|^{1/2}$ の円とします。$P_\nu(1)=1$ とすでに分かっているので $z\neq1$ として構いません。
この円が「$1,z$ を囲み、$-1$ を囲まない」という条件を満たさねばなりません。$z$ を中心としているので $z$ を囲むのは当然として、次の条件が付されます。\begin{equation}|z-1|<|z^2-1|^{1/2}\;\land\;|z+1|>|z^2-1|^{1/2}\tag{9}\end{equation}この2つの不等式はそれぞれ2乗することで次のように簡単に整理されます。\begin{equation}|z-1|<|z+1|\tag{10}\end{equation}(10)は\begin{equation}\mathfrak{R}z>0\tag{11}\end{equation}と同値です。
つまり目的の置換をしたければ $\mathfrak{R}z>0$ という条件を満たす必要があるのです。なので$$-\frac{\pi}{2}<\arg z<\frac{\pi}{2}\;,\; z\neq 0$$として話を進めます。
さて、目的としていた置換をしましょう。\begin{equation}t=z+(z^2-1)^{1/2}e^{i\phi}\tag{12}\end{equation}とおき、$\phi$ を $-\pi$ から $\pi$ まで変化させます。すると先ほどと同様の式変形によって\begin{equation}P_\nu(z)=\frac{1}{\pi}\int_0^{\pi}\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu d\phi\tag{13}\end{equation}
これで完成といいたいところですが、今回は$$\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu$$が一般に多価関数です。例えば\begin{equation}\left[z+(z^2-1)^{1/2}\cos\phi\right]^{1/3}=\left\{\begin{array}{l}a\\ ae^{\frac{2}{3}\pi i}\\ ae^{\frac{4}{3}\pi i}\end{array}\right.\tag{14}\end{equation}のような感じです。どれを選ぶか(どの枝をとるか)によって(13)右辺の結果は明らかに変わってきます。それではダメなので、いずれか指定する必要があります。
(14)の3つの値を生じさせる機械的な方法は$$z+(z^2-1)^{1/2}\cos\phi=\left[z+(z^2-1)^{1/2}\cos\phi\right]e^{2m\pi i}\;,\quad m\in\ZZ$$としてやることです。この右辺を1/3乗すると(14)の3個が出現します。$\nu$ 乗であれば\begin{equation}\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu=\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu e^{2m\pi i\nu}\tag{15}\end{equation}と書き換えることで多価性を表現できます。(15)左辺の $\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu$ は値の「集まり」です。対して(15)右辺の $\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu$ は、その偏角を1つに指定することで1つの値に決まっており、$e^{2m\pi i\nu}$ を付して値の「集まり」としています。
$\phi$ を変化させると $z+(z^2-1)^{1/2}\cos\phi$ は $z-(z^2-1)^{1/2}$ と $z+(z^2-1)^{1/2}$ を結ぶ直線を往復します。この直線は原点を通らないので、$z+(z^2-1)^{1/2}\cos\phi$ の偏角の変化は $\pi$ 未満です。
ここで(15)右側の $\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu$ の偏角を、$\phi=\frac{\pi}{2}$ としたときに $z^\nu$ の偏角と一致するようにとることにします。
つまり\begin{equation}P_\nu(z)=\frac{e^{2m\pi i\nu}}{\pi}\int_0^{\pi}\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu d\phi\tag{16}\end{equation}ただし $\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu$ の偏角を、$\phi=\frac{\pi}{2}$ としたときに $z^\nu$ の偏角と一致するようにとる。というわけです。
あとは $m$ を確定させましょう。$z\to 1$(偏角0)とすると\begin{equation}P_\nu(z)\to\frac{e^{2m\pi i\nu}}{\pi}\int_0^{\pi}1^\nu d\phi\tag{17}\end{equation}ここで右辺の「1」の偏角は $0$ と指定しているので $1^\nu$ の偏角は $0\times\nu=0$ です。したがって $1^\nu=1$ であり、$P_\nu(1)=1$ と比較すると $m=0$ と決まります。
以上により
$\mathfrak{R}z>0$ , $\nu\in\CC$ ,
$$P_\nu(z)=\frac{1}{\pi}\int_0^\pi\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu d\phi$$
ただし $(z^2-1)^{1/2}$ の枝は任意にとってよく、$[z+(z^2-1)^{1/2}\cos\phi]^\nu$ の枝は $\phi=\frac{\pi}{2}$ のときに $z^\nu$ と偏角が一致するようにとる。
偏角の話はややこしいですが、わりと自然な決め方をしているということは後述の例でも確認できると思います。あまり身構えなくても大丈夫。
定理3でもなお $\phi\to\pi -\phi$ なる置換によって\begin{equation}P_\nu(z)=\frac{1}{\pi}\int_0^{\pi}\left[z-(z^2-1)^{1/2}\cos\phi\right]^\nu d\phi\tag{18}\end{equation}とも書けます。よって $(z^2-1)^{1/2}$ の枝はどちらでもよいということです。
簡単な例で確認しましょう。$\nu=1/2$ であれば2通りの枝(正負)から1つを選ぶことになります。$z=2$ であれば $\arg z=0$ なので $\arg z^\frac{1}{2}=0$ です。$$P_{\frac{1}{2}}(2)=\frac{1}{\pi}\int_0^\pi \left(2+\sqrt{3}\cos\phi\right)^\frac{1}{2}d\phi$$$\left(2+\sqrt{3}\cos\phi\right)^\frac{1}{2}$ の枝は $\pm\sqrt{2+\sqrt{3}\cos\phi}$ のいずれか(偏角 $0$ or $\pi$ )です。今の場合は $\phi=\frac{\pi}{2}$ としたときに偏角が0となるようにしなければなりません。したがって正のほうをとって$$P_{\frac{1}{2}}(2)=\frac{1}{\pi}\int_0^\pi \sqrt{2+\sqrt{3}\cos\phi}\: d\phi$$となります。この積分は初等的には計算できませんが、楕円積分で書けるかもしれません。
次に $\nu=i$ , $z=e^{\frac{\pi}{4}i}$ としましょう。複素数乗の偏角は主値をとることにすれば $\arg z^i = 0$ となります。よって問題の枝もこれに合わせて主値をとることになるだけです。あまり気を使わなくて大丈夫。
定理1より
$$P_\nu(z)=P_{-\nu-1}(z)$$
これと定理3を合わせると
$\mathfrak{R}z>0$ , $\nu\in\CC$ , $$P_\nu(z)=\frac{1}{\pi}\int_0^\pi\frac{d\phi}{\left[z+(z^2-1)^{1/2}\cos\phi\right]^{\nu+1}}$$ただし $(z^2-1)^{1/2}$ の枝は任意にとってよく、$[z+(z^2-1)^{1/2}\cos\phi]^{-\nu-1}$ の枝は $\phi=\frac{\pi}{2}$ のときに $z^{-\nu-1}$ と偏角が一致するようにとる。
$$P_\nu(z)=z^\nu \: F\left[\begin{matrix}-\frac{\nu}{2} , \frac{-\nu+1}{2}\\1\end{matrix};1-\frac{1}{z^2}\right]$$
定理3からスタートする。$\cos\phi$ についての展開を目指す。$$P_\nu(z)=\frac{z^\nu}{\pi}\int_0^\pi\left[1+\frac{(z^2-1)^{1/2}}{z}\cos\phi\right]^\nu d\phi$$被積分関数を二項級数に展開すると$$P_\nu(z)=\frac{z^\nu}{\pi}\int_0^\pi\sum_{n=0}^\infty \frac{(-\nu)_n}{n!}\left(-\frac{(z^2-1)^{1/2}}{z}\cos\phi\right)^n d\phi$$積分と総和を入れ替えて$$P_\nu(z)=\frac{z^\nu}{\pi}\sum_{n=0}^\infty \frac{(-\nu)_n}{n!}\left(-\frac{(z^2-1)^{1/2}}{z}\right)^n\int_0^\pi \cos^n\phi d\phi$$ここで$$\int_0^\pi \cos^n\phi d\phi=(1+(-1)^n)\int_0^\frac{\pi}{2} \cos^n\phi d\phi$$なので級数は偶数項のみになる。$$P_\nu(z)=\frac{2z^\nu}{\pi}\sum_{n=0}^\infty \frac{(-\nu)_{2n}}{(2n)!}\left(1-\frac{1}{z^2}\right)^n\int_0^\frac{\pi}{2} \cos^{2n}\phi d\phi$$積分を実行して\begin{align}P_\nu(z)&=z^\nu\sum_{n=0}^\infty \frac{(-\nu)_{2n}}{(2n)!}\left(1-\frac{1}{z^2}\right)^n\frac{(2n-1)!!}{(2n)!!}\\&=z^\nu\sum_{n=0}^\infty \frac{(-\nu)_{2n}}{(2n)!!^2}\left(1-\frac{1}{z^2}\right)^n\\&=z^\nu\sum_{n=0}^\infty \frac{(-\nu)_{2n}}{2^{2n}n!^2}\left(1-\frac{1}{z^2}\right)^n\\&=z^\nu\sum_{n=0}^\infty \frac{(\frac{-\nu}{2})(\frac{-\nu+1}{2})\cdots(\frac{-\nu+2n-1}{2})}{n!^2}\left(1-\frac{1}{z^2}\right)^n\\&=z^\nu\sum_{n=0}^\infty \frac{(\frac{-\nu}{2})_n(\frac{-\nu+1}{2})_n}{n!^2}\left(1-\frac{1}{z^2}\right)^n\end{align}となって超幾何関数の表示を得る。
次回はこちら:
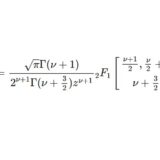 ルジャンドル関数の基礎7~第2種ルジャンドル関数の定義と超幾何級数
ルジャンドル関数の基礎7~第2種ルジャンドル関数の定義と超幾何級数
第5版です。いわずと知れた名著。特殊関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。