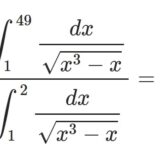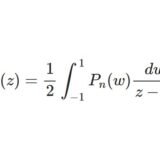前回はこちら：
ルジャンドル関数の基礎６～超幾何関数による表示・ラプラスの積分表示
もくじ
前回までは第1種ルジャンドル関数 $P_\nu(z)$ について学びました。$P_\nu(z)$ は次の複素積分で表現することにより、$z$ , $\nu$ を複素平面の広い範囲で定義することができました。
$$P_\nu(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\quad(\nu\in\CC\;,\, z\neq -1)$$ただし経路 $C$ は $1,z$ を時計回りに囲むが $-1$ は囲まない．
$\nu$ が非整数の場合、$t$ 平面には $1$ と $z$ を結ぶ切断、$-1$ と $-\infty$ を結ぶ切断を入れる．
この $P_\nu(z)$ はルジャンドルの微分方程式を満足します：
\begin{equation}(1-z^2)y^{\prime\prime}-2zy'+\nu(\nu+1)y=0\end{equation}
なので $P_\nu(z)$ は定義１式の特殊解の１つとなります。定数倍しても解ですから、\begin{equation}\oint_C\frac{(t^2-1)^\nu}{(t-z)^{\nu+1}}dt\tag{1}\end{equation}は解です。
(1)がこの微分方程式の解になることをこちらの記事で示しました。その記事を見れば、より一般に次のような事実がいえることが分かります。
\begin{equation}\oint_X\frac{(t^2-1)^\nu}{(t-z)^{\nu+1}}dt\tag{2}\end{equation}はルジャンドル微分方程式の解である。ただし周回経路 $X$ は、被積分関数の値が始点と終点で一致するようにとられたものである。
「周回経路なら始点と終点で一致しているのは当たり前では？」と思われるかもしれませんが、被積分関数が分岐点をもつため、工夫した経路を設定しないとそうはならないのです。先の経路 $C$ はこれを満たしています。
ここまでの話を念頭に入れつつ、新しい関数を定義します。
ルジャンドルの微分方程式の解として $P_\nu(z)$ が見つかっていますが、解はほかにもあります。補題２の条件を満たす新しい経路 $D$ を設定して次のように第2種ルジャンドル関数を定義します。
$z\in\CC$ かつ $z\notin[-1,1]$ , $|\arg z|\le\pi$において\begin{align}Q_\nu(z)& :=\frac{1}{4i\sin\pi\nu}\oint_D\frac{(t^2-1)^\nu}{2^\nu(z-t)^{\nu+1}}dt\quad(\nu\in\CC\setminus\ZZ)\tag{3}\\Q_\nu(z)& :=\frac{1}{2}\int_{-1}^1\frac{(t^2-1)^\nu}{2^\nu(z-t)^{\nu+1}}dt\quad(\nu\in\ZZ_{\ge0})\tag{4}\end{align}ここで $t=\pm 1$ を焦点とし、内部に $z$ を含まない楕円 $K$ を考える。楕円 $K$ の内部に周回経路 $D$ を設定する。$D$ は「横８の字型(figure-eight)」で、$t=1$ を時計回りにまわり、$t=-1$ を反時計回りにまわる経路である。また実軸と $1$ の右側で $D$ が交差する点の偏角は $\arg(t+1)=0$ , $\arg(t-1)=0$ とする。
また定義１より $Q_\nu(z)=Q_{-\nu-1}(z)$ とできるため、$\nu$ が負整数でも定義される。
難解な定義ですが、$z$ , $\nu$ を複素数の範囲で扱うにはこのようになります。(3)(4)と分けて定義されていますが、後の解説を読めば起源は同一であることが分かります。実際、(3)で $\nu\to n$ の極限をとると(4)になることが後でわかります。
積分経路について
さて定義３(3)式を見て、$Q_\nu(z)$ がどんな関数なのか…さっぱり掴めません。$z$ は実軸上の $[-1,1]$ にはいないので、十分小さな楕円を取れば $z$ を含まないようにできます。その楕円の内部に経路 $D$ を描きます。
経路 $D$ は次のようになります。
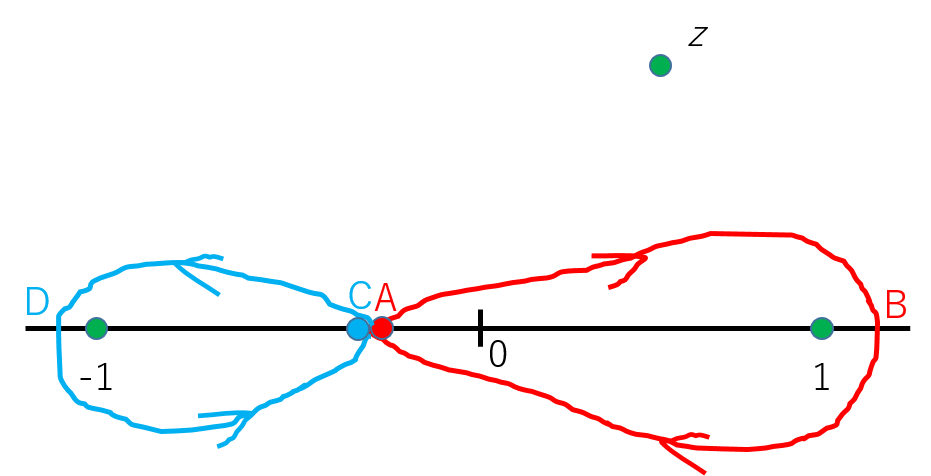
被積分関数を見れば分かるように、$t=\pm 1$ , $z$ が分岐点となっています。$z$ は経路の外にあるので気になりません。$[-1,1]$ に切断(branch cut)を入れ、$1$ や $-1$ をまわると別の葉に移るようになっています（この辺の話はこちらも参考に。分岐点の話は分からなくても、雰囲気で計算はできるので、読み流して大丈夫）。また８の字の「交差点」が $0$ より左側になっていますが、$0$ に重なっていても今は問題ありません。「交差点」といっても赤線と青線は別世界なので実際には交差してませんが。
定義３より図のBで $\arg(t+1)=0$ , $\arg(t-1)=0$ です。よって図のAでは $\arg(t+1)=0$ , $\arg(t-1)=\pi$ です。このAをスタートとしましょう。A→B→Cで $1$ を時計回りに１周したのでCでの偏角は $\arg(t+1)=0$ , $\arg(t-1)=-\pi$ です。AとCは同じ点なのに $\arg(t-1)$ が異なっています。つまりCから先は別の葉です。C→D→Aとまわると $-1$ を反時計回りに1周したので $\arg(t+1)=2\pi$ , $\arg(t-1)=-\pi$ で終わりです。
さて終点のAでの偏角は始点のAでの偏角と異なっているように見えます。しかし被積分関数全体としてみると\begin{equation}始点:\frac{(t+1)^\nu\left((1-t)e^{\pi i}\right)^\nu}{(z-t)^{\nu+1}}\quad 終点:\frac{\left((t+1)e^{2\pi i}\right)^\nu\left((1-t)e^{-\pi i}\right)^\nu}{(z-t)^{\nu+1}}\tag{5}\end{equation}で両者は一致しています。つまりこの8の字型経路は被積分関数の値が指定と終点で一致するようにとられていることになります。
なので青線は別世界なのですが、終点Aで元の世界に戻るのです。ちゃんと周回している！
微分方程式を満たす
(3)がルジャンドルの微分方程式を満たすかを確認します。つい先ほどの話から、補題２によりただちに(3)式は微分方程式を満たします。(4)は実は(3)の積分から導出されたもので、これも微分方程式を満たします。あとで解説します。
定義３(3)に現れる積分を計算しましょう。
経路と次数の限定で扱いやすくする
ここで経路 $D'$ を設定します。$D'$ は経路 $D$ と同じ条件で、かつ $1$ や $-1$ をまわるときは小円を描き、その間は実軸に沿ってまっすぐ進むとします。経路図のAを-1ぎりぎりまで近づけます。また、\begin{equation}\mathfrak{R}(\nu+1)>0\tag{6}\end{equation}を仮定します。
このように限定された場合、問題の積分は次のように計算できます。まず $\arg(t+1)=0$ , $\arg(t-1)=\pi$ を保って $1$ へ向かい、$1$ を小円で回ります。すると $1$ まわりの偏角が $2\pi$ 減少して $\arg(t+1)=0$ , $\arg(t-1)=-\pi$ になり、そのまま実軸に沿って $-1$ へ向かいます。その後 $-1$ を小円でまわります。このとき $-1$ まわりの偏角が $2\pi$ 増加します。よって\begin{align}&\oint_{D'}\frac{(t^2-1)^\nu}{(z-t)^{\nu+1}}dt\\ &= \int_{-1}^1\frac{(t+1)^\nu\left((1-t)e^{\pi i}\right)^\nu}{(z-t)^{\nu+1}}dt +\underbrace{\int_{\pi}^{-\pi}\frac{(2+\epsilon e^{i\t})^\nu(\epsilon e^{i\t})^\nu}{(z-1-\epsilon e^{i\t})^{\nu+1}}i\epsilon e^{i\t}d\t}_{t=1+\epsilon e^{i\t}}\\ &\quad+ \int_{1}^{-1}\frac{(t+1)^\nu\left((1-t)e^{-\pi i}\right)^\nu}{(z-t)^{\nu+1}}dt+\underbrace{\int_0^{2\pi}\frac{(\epsilon e^{i\t})^\nu\left((2-\epsilon e^{i\t})e^{-\pi i}\right)^\nu}{(z+1-\epsilon e^{i\t})^{\nu+1}}i\epsilon e^{i\t}d\t}_{t=-1+\epsilon e^{i\t}}\\ &= (e^{\pi i\nu}-e^{-\pi i\nu})\int_{-1}^1\frac{(1-t^2)^\nu}{(z-t)^{\nu+1}}dt \\&\quad +i\epsilon^{\nu+1}2^\nu\int_{\pi}^{-\pi}\frac{e^{i(\nu+1)\t}}{(z-1)^{\nu+1}}d\t + i\epsilon^{\nu+1}2^\nu e^{-\pi i\nu}\int_0^{2\pi}\frac{ e^{i(\nu+1)\t} }{(z+1)^{\nu+1}}d\t\end{align}(6)を仮定したので2,3番目の積分は消えて\begin{equation}\oint_{D'}\frac{(t^2-1)^\nu}{(z-t)^{\nu+1}}dt=2i\sin\pi\nu\int_{-1}^1\frac{(1-t^2)^\nu}{(z-t)^{\nu+1}}dt\tag{7}\end{equation}計算の過程で $1-t$ や $1+t$ の偏角は $e^{\pi i}$ などの形で外に出したので(7)では $\arg(t+1)=0$ , $\arg(1-t)=0$ です。
定義３の(3)を再掲すると\begin{equation}Q_\nu(z)=\frac{1}{4i\sin\pi\nu}\oint_D\frac{(t^2-1)^\nu}{2^\nu(z-t)^{\nu+1}}dt\tag{8}\end{equation}でしたから(7)より\begin{equation}Q_\nu(z)=\frac{1}{2}\int_{-1}^1\frac{(1-t^2)^\nu}{2^\nu(z-t)^{\nu+1}}dt\tag{9}\end{equation}(7)(8)を見れば、$\nu\to n$ でやはり(9)が得られます。
以上より
$\mathfrak{R}(\nu+1)>0$ で次が成り立つ：$$Q_\nu(z)=\frac{1}{2}\int_{-1}^1\frac{(1-t^2)^\nu}{2^\nu(z-t)^{\nu+1}}dt$$だたし $\arg(t+1)=0$ , $\arg(1-t)=0$ .
例えば$$Q_0(z)=\frac{1}{2}\log\frac{z+1}{z-1}$$などとなります。
歳2種ルジャンドル関数を超幾何関数で表します。以下、\begin{equation}|z|>1\tag{10}\end{equation}とします。このとき$$(z-t)^{-\nu-1}=z^{-\nu-1}\left(1-\frac{t}{z}\right)^{-\nu-1}$$で、さらに二項級数に展開すると\begin{equation}(z-t)^{-\nu-1}=z^{-\nu-1}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!}\left(\frac{t}{z}\right)^n\tag{11}\end{equation}
(11)は絶対一様収束することを示します。(10)と楕円 $K$ の取り方（定義３）により $\frac{|t|}{|z|}\le\d<1$ なる $\d$ が存在します。$$\sum\left|\frac{(\nu+1)_n}{n!}\left(\frac{t}{z}\right)^n\right|\le\sum\frac{|(\nu+1)_n|}{n!}\d^n$$この右辺に関してダランベールの収束判定法を使うと$$\frac{a_{n+1}}{a_n}=\frac{|\nu+n+1|}{n+1}\d\xrightarrow[]{n\to\infty}\d<1$$で収束します。よってワイエルシュトラスのM判定法により(11)は絶対一様収束します。
(11)の右辺は一様収束するので項別積分可能です。
以下、２つのバージョンを解説します。
分かりやすいバージョン
$\mathfrak{R}(\nu+1)>0$ に限定すると、比較的平易に $Q_\nu(z)$ を級数表示できます。定理４に(11)を適用して\begin{equation}Q_\nu(z)=\frac{1}{2^{\nu+1}z^{\nu+1}}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!z^n}\int_{-1}^1t^n(1-t^2)^\nu dt\tag{12}\end{equation}偶奇性によって$$Q_\nu(z)=\frac{1}{2^{\nu}z^{\nu+1}}\sum_{n=0}^\infty\frac{(\nu+1)_{2n}}{(2n)!z^{2n}}\int_{0}^1t^{2n}(1-t^2)^\nu dt$$$t^2=u$ と置換して$$Q_\nu(z)=\frac{1}{2^{\nu+1}z^{\nu+1}}\sum_{n=0}^\infty\frac{(\nu+1)_{2n}}{(2n)!z^{2n}}\int_{0}^1u^{n-\frac{1}{2}}(1-u)^\nu du$$$n+\frac{1}{2}>0$ , $\mathfrak{R}(\nu+1)>0$ よりベータ関数の積分表示が適用できますので$$Q_\nu(z)=\frac{1}{2^{\nu+1}z^{\nu+1}}\sum_{n=0}^\infty\frac{(\nu+1)_{2n}}{(2n)!z^{2n}}\frac{\G(n+\frac{1}{2})\G(\nu+1)}{\G(\nu+n+\frac{1}{2})}$$ガンマ関数をポッホハマー記号になおしていくと$$Q_\nu(z)=\frac{\sqrt{\pi} \G(\nu+1)}{2^{\nu+1}z^{\nu+1}\G(\nu+\frac{3}{2})}\sum_{n=0}^\infty\frac{(\frac{1}{2})_n(\nu+1)_{2n}}{(2n)!(\nu+\frac{3}{2})_n}\frac{1}{z^{2n}}$$ここで$$(2n)!=2^{2n}n!\left(\frac{1}{2}\right)_n$$$$(\nu+1)_{2n}=2^{2n}\left(\frac{\nu+1}{2}\right)_n\left(\frac{\nu+2}{2}\right)_n$$を用いて\begin{equation}Q_\nu(z)=\frac{\sqrt{\pi} \G(\nu+1)}{2^{\nu+1}z^{\nu+1}\G(\nu+\frac{3}{2})}\sum_{n=0}^\infty\frac{\left(\frac{\nu+1}{2}\right)_n\left(\frac{\nu}{2}+1\right)_n}{(\nu+\frac{3}{2})_nn!}\frac{1}{z^{2n}}\tag{13}\end{equation}以上より$\mathfrak{R}(\nu+1)>0$ において次が成り立ちます。\begin{equation}Q_\nu(z)=\frac{\sqrt{\pi} \G(\nu+1)}{2^{\nu+1}z^{\nu+1}\G(\nu+\frac{3}{2})}{}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix};\frac{1}{z^2}\right]\tag{14}\end{equation}
難しいけどより一般的なバージョン
(14)は$\mathfrak{R}(\nu+1)>0$ の制限を取り払っても成立します。それを示しましょう。ここでも $|z|>1$ です。
もはや定理４は使えませんので、定義３(3)に立ち返ります。これに(11)を適用すると\begin{equation}Q_\nu(z)=\frac{1}{4i\sin\pi\nu\cdot 2^\nu z^{\nu+1}}\sum_{n=0}^\infty\frac{(\nu+1)_n}{n!z^n}\oint_D t^n(t^2-1)^\nu dt\tag{15}\end{equation}
では(15)の積分を詳しく見ましょう。もう1度、経路 $D$ の画像を貼っておきます。
Aの位置をあえて $0$ より左にずらしています（このあと $0$ が分岐点になるので、$0$ を通らないようにしている）。目標はベータ関数に帰着させることなので、$t^2=u$ と置換します。すると\begin{equation}\oint_D t^n(t^2-1)^\nu dt=\frac{1}{2}\oint_E u^\frac{n-1}{2}(u-1)^\nu du\tag{16}\end{equation}ここで $u$ 平面における経路 $E$ は図2のようになります。分岐点は $0$ と $1$ です。スタート地点はAで $\arg u=2\pi$ , $\arg(u-1)=\pi$ です。A→B→C→D→E→F→Aと戻る間に、$0$ を負方向に2周、$1$ を正方向と負方向に1周ずつしています。(16)の被積分関数はこの経路で終点と始点の値は一致します。
図2の経路を次のように変形します。
$0$ のすぐ右にあるAをスタートし、$0$ を負方向に小円で1周、実軸に沿って $1$ へ行く。$1$ を負方向に1周して、実軸に沿って $0$ へ行く。$0$ を負方向に1周して同様に $1$ へ向かい、$1$ を正方向に1周して $0$ すなわちAへ帰る。
すると次のように計算できます。$[0,1]$ の区間は本当は $[\epsilon,1-\epsilon]$ です。\begin{align}&\oint_E u^\frac{n-1}{2}(u-1)^\nu du \\ &=\underbrace{\int^{(0^-)}_{2\pi\to 0}u^{\frac{n-1}{2}}\left((1-u)e^{\pi i}\right)^\nu du}_{P}+\int_0^1x^{\frac{n-1}{2}}\left((1-x)e^{\pi i}\right)^\nu dx \\ &\quad +\underbrace{\int^{(1^-)}_{\pi\to -\pi}u^{\frac{n-1}{2}}(u-1)^\nu du}_{Q}+\int_1^0x^{\frac{n-1}{2}}\left((1-x)e^{-\pi i}\right)^\nu dx\\ &\quad + \underbrace{\int^{(0^-)}_{0\to -2\pi}u^{\frac{n-1}{2}}\left((1-u)e^{-\pi i}\right)^\nu du}_{R} + \int_0^1\left(xe^{-2\pi i}\right)^{\frac{n-1}{2}}\left((1-x)e^{-\pi i}\right)^\nu dx\\ &\quad + \underbrace{\int^{(1^+)}_{-\pi\to \pi}\left(ue^{-2\pi i}\right)^{\frac{n-1}{2}}(u-1)^\nu du}_{S} + \int_1^0\left(xe^{-2\pi i}\right)^{\frac{n-1}{2}}\left((1-x)e^{\pi i}\right)^\nu dx\end{align}ここで $\displaystyle\int_{a\to b}^{(z^+)}$ は、「$z$ を正方向（＋）に回り、$u-z$ の偏角が $a$ から $b$ に変化する」という意味です。
積分 $P$ は、経路を逆にして$$P=-e^{\pi i\nu}\int^{(0^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du$$積分 $S$ は $u-1$ の偏角 $-\pi i$ をずらして$$S=-(-1)^n e^{-\pi i\nu}\int^{(1^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du$$積分 $R$ では、経路を逆にして $u$ の偏角 $-2\pi$ をずらすと$$R=-e^{-\pi i\nu}\int^{(0^+)}_{0\to 2\pi}(ue^{-2\pi i})^{\frac{n-1}{2}}(1-u)^\nu du=(-1)^ne^{-\pi i\nu}\int^{(0^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du$$積分 $Q$ では、経路を逆にして $u-1$ の偏角 $-\pi i$ をずらして$$Q=-e^{-\pi i\nu}\int^{(1^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du$$
以上より\begin{align}\oint_E u^\frac{n-1}{2}(u-1)^\nu du &=(e^{\pi i\nu}-e^{-\pi i\nu})\left(1+(-1)^n\right)\int_0^1x^{\frac{n-1}{2}}(1-x)^\nu dx\\&\quad -\left(e^{\pi i\nu}-(-1)^ne^{-\pi i\nu}\right)\int^{(0^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du\\&\quad -e^{-\pi i\nu}\left(1+(-1)^n\right)\int^{(1^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du\tag{17}\end{align}(17)から分かるように、$n$ が奇数なら1行目と3行目はただちにゼロ、2行目についても $u=0$ が分岐点にならないのでコーシーの積分定理によりゼロ。したがって $n$ が偶数のときのみ考えればいいです。
$n$:odd であれば$$\oint_E u^\frac{n-1}{2}(u-1)^\nu du = 0$$$n$:even であれば $n=2m$ として\begin{align}\oint_E u^\frac{2m-1}{2}(u-1)^\nu du &=4i\sin\pi\nu\int_0^1x^{\frac{2m-1}{2}}(1-x)^\nu dx\\&\quad -2i\sin\pi\nu\int^{(0^+)}_{0\to 2\pi}u^{\frac{2m-1}{2}}(1-u)^\nu du\\&\quad -2e^{-\pi i\nu}\int^{(1^+)}_{0\to 2\pi}u^{\frac{2m-1}{2}}(1-u)^\nu du\end{align}
ベータ関数のポッホハマー積分との比較
補題５とベータ関数の比較をします。ベータ関数のポッホハマーによる拡張された積分表示は
$\a,\b\in\CC$ とする。$$B(\a,\b)=-\frac{e^{-\pi i(\a+\b)}}{4\sin\pi\a\sin\pi\b}\oint_Pu^{\a-1}(1-u)^{\b-1}dt$$ただし経路 $P$ はポッホハマー積分路であり、$1$ を正方向に回り、$0$ を正方向に回り、$1$ を負方向にまわり、$0$ を負方向に回る周回経路である。スタート地点は $0$ と $1$ の間であり、その点での偏角は $\arg u=0$ , $\arg(1-u)=0$ とする。
これに $\a=\frac{n+1}{2}$ , $\b=\nu+1$ とした場合、(17)と同様の計算過程を経て\begin{align}\oint_P u^\frac{n-1}{2}(1-u)^\nu du &=4e^{\frac{n-1}{2}\pi i}e^{\pi i\nu}\cos\frac{n\pi}{2}\sin\pi\nu\int_0^1x^{\frac{n-1}{2}}(1-x)^\nu dx\\&\quad + (e^{2\pi i\nu}-1)\int^{(0^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du\\ &\quad+\left(1+(-1)^n\right)\int^{(1^+)}_{0\to 2\pi}u^{\frac{n-1}{2}}(1-u)^\nu du\tag{18}\end{align}(18)は $n$ が奇数のときにゼロであり、偶数では $n=2m$ として\begin{align}\oint_P u^\frac{2m-1}{2}(1-u)^\nu du &=-4i e^{\pi i\nu}\sin\pi\nu\int_0^1x^{\frac{2m-1}{2}}(1-x)^\nu dx\\&\quad + (e^{2\pi i\nu}-1)\int^{(0^+)}_{0\to 2\pi}u^{\frac{2m-1}{2}}(1-u)^\nu du\\ &\quad+2\int^{(1^+)}_{0\to 2\pi}u^{\frac{2m-1}{2}}(1-u)^\nu du\tag{19}\end{align}補題５と(19)を比べると
$$\oint_E u^\frac{n-1}{2}(u-1)^\nu du =-e^{-\pi i\nu}\oint_P u^\frac{n-1}{2}(1-u)^\nu du$$ただし $n$ が奇数では両辺ともゼロ。
以上から(16)により\begin{equation}\oint_D t^n(t^2-1)^\nu dt=\left\{\begin{array}{c}-\displaystyle\frac{e^{-\pi i\nu}}{2}\oint_P u^\frac{n-1}{2}(1-u)^\nu du & (n:\mathrm{even})\\0 & (n:\mathrm{odd})\end{array}\right.\tag{20}\end{equation}定義６より\begin{equation}\oint_D t^n(t^2-1)^\nu dt=\left\{\begin{array}{c}2i\sin\pi\nu \cdot\: B\left(\displaystyle\frac{n+1}{2},\nu+1\right) & (n:\mathrm{even})\\0 & (n:\mathrm{odd})\end{array}\right.\tag{21}\end{equation}これを(15)に用いると\begin{equation}Q_\nu(z)=\frac{\sqrt{\pi} \G(\nu+1)}{2^{\nu+1}z^{\nu+1}\G(\nu+\frac{3}{2})}{}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix};\frac{1}{z^2}\right]\tag{22}\end{equation}で(14)と一致します。
今回は(14)と違って $\nu$ に制限はありません。まとめると
$|z|>1$ , $\nu\in\CC\setminus \ZZ_{<0}$ ,$$Q_\nu(z)=\frac{\sqrt{\pi} \G(\nu+1)}{2^{\nu+1}\G(\nu+\frac{3}{2})z^{\nu+1}}{}_2F_1\left[\begin{matrix}\frac{\nu+1}{2},\frac{\nu}{2}+1\\\nu+\frac{3}{2}\end{matrix};\frac{1}{z^2}\right]$$
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
