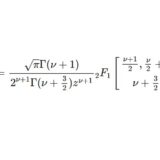前回はこちら:
ルジャンドル関数の基礎7~第2種ルジャンドル関数の定義と超幾何級数
今回は第2種ルジャンドル関数の漸化式や公式をいくつか紹介します.割と端折っている部分もあります.詳しく知りたい場合は記事下部の参考文献に,より多くの公式や詳細な解説があります.
第2種ルジャンドル関数は $z\in\CC$ ただし実軸上の $[-1,1]$ を除いて\begin{equation}Q_\nu(z)=\frac{1}{4i\sin\pi\nu}\oint_D\frac{(t^2-1)^\nu}{2^\nu(z-t)^{\nu+1}}dt\quad(\nu\in\CC\setminus\ZZ_{<0})\tag{1}\end{equation}で定められました.この積分の形は第1種ルジャンドル関数 $P_\nu(z)$ のもの\begin{equation}P_\nu(z)=\frac{1}{2\pi i}\oint_C\frac{(t^2-1)^\nu}{2^\nu(t-z)^{\nu+1}}dt\tag{2}\end{equation}と似た形をしています.なので $P_\nu(z)$ の漸化式を導出したときと全く同様に $Q_\nu(z)$ についても漸化式をつくることができます.
$P_\nu(z)$ についての漸化式はこちらで導いたように\begin{align} & P'_{\nu+1}(z)-zP'_\nu(z)=(\nu+1)P_\nu(z)\tag{3a}\\& (\nu+1)P_{\nu+1}(z)=(2\nu+1)zP_\nu(z)-\nu P_{\nu-1}(z)\tag{3b}\\& zP'_\nu(z)=\nu P_\nu(z)+ P'_{\nu-1}(z)\tag{3c}\\& P'_{\nu+1}(z)-P'_{\nu-1}(z)=(2\nu +1) P_\nu(z)\tag{3d}\\& (z^2-1)P'_{\nu}(z) =\nu z P_\nu(z)-\nu P_{\nu-1}(z)\tag{3e}\end{align}同様にして
\begin{align} & Q'_{\nu+1}(z)-zQ'_\nu(z)=(\nu+1)Q_\nu(z)\tag{4a}\\& (\nu+1)Q_{\nu+1}(z)=(2\nu+1)zQ_\nu(z)-\nu Q_{\nu-1}(z)\tag{4b}\\& zQ'_\nu(z)=\nu Q_\nu(z)+ Q'_{\nu-1}(z)\tag{4c}\\& Q'_{\nu+1}(z)-Q'_{\nu-1}(z)=(2\nu +1) Q_\nu(z)\tag{4d}\\& (z^2-1)Q'_{\nu}(z) =\nu z Q_\nu(z)-\nu Q_{\nu-1}(z)\tag{4e}\end{align}
ただし(1)式は $\nu$ が負整数の場合を除くため,定理1のおのおのの $Q_\nu$ の添え字が負整数でないときに限ります.例えば(4b)で $\nu=0$ とはできません.
$\mathfrak{R}\nu> -1$ のとき,定理1は\begin{equation}Q_\nu(z)=\frac{1}{2}\int_{-1}^1\frac{(1-t^2)^\nu}{2^\nu(z-t)^{\nu+1}}dt\tag{5}\end{equation}と改めることができました(前回).これをまともに計算することで\begin{equation}Q_0(z) = \frac{1}{2}\log\frac{z+1}{z-1}\tag{6}\end{equation}あるいは\begin{equation}Q_1(z) = \frac{z}{2}\log\frac{z+1}{z-1}-1\tag{7}\end{equation}となります.これらから漸化式によって $Q_2(z)$ を求めることができます.
$\nu=n\in\ZZ_{>0}$ とします.第1種ルジャンドル関数 $P_n(z)$ はこのとき「ルジャンドル多項式」といわれます.ルジャンドル多項式においては次のロドリグの公式が知られます.\begin{equation}P_n(z)=\frac{1}{2^nn!}\frac{d^n}{dz^n}(z^2-1)^n\tag{8}\end{equation}これの $Q_n(z)$ バージョンを導出しましょう.
$w(z)$ の微分方程式\begin{equation}(1-z^2)w''+2(n-1)zw'+2nw=0\tag{9}\end{equation}を考えます.これを微分すると$$(1-z^2)w'''+2(n-2)zw''+((2n)+(2n-2))w'=0$$さらに微分すると$$(1-z^2)w''''+2(n-3)zw''+((2n)+(2n-2)+(2n-4))w''=0$$$n-1$ 階微分は$$(1-z^2)w^{(n+1)}+n(n+1)w^{(n-1)}=0$$もう1度微分すると\begin{equation}(1-z^2)w^{(n+2)}-2zw^{(n+1)}+n(n+1)w^{(n)}=0\tag{10}\end{equation}ところでルジャンドルの微分方程式は次のようなものです:\begin{equation}(1-z^2)y^{\prime\prime}-2zy'+n(n+1)y=0\tag{11}\end{equation}(10)(11)を見比べると $w^{(n)}$ は(11)の解です.
ところで(9)の方程式に戻りますが,$$w(z)=(z^2-1)^n\;,\; w(z)=(z^2-1)^n\int_z^\infty\frac{dt}{(t^2-1)^{n+1}}$$を代入してみるとこれらは(9)の特殊解になっています.よってこれらの $n$ 階微分が(11)の解になっているはずですから$$\frac{d^n}{dz^n}(z^2-1)^n$$および$$\frac{d^n}{dz^n}\left[(z^2-1)^n\int_z^\infty\frac{dt}{(t^2-1)^{n+1}}\right]$$はルジャンドルの微分方程式(11)の解です.前者は(8)から分かるように $P_n(z)$ (の定数倍)に一致します.では後者は何でしょう?
\begin{equation}f(z):=(z^2-1)^n\int_z^\infty\frac{dt}{(t^2-1)^{n+1}}\tag{12}\end{equation}とおきましょう.目標は(12)を $1/z$ についての展開で表すことです.$t=zu$ と置換すると$$f(z)=z(z^2-1)^n\int_1^\infty\frac{1}{(uz)^{2n+2}}\left(1-\frac{1}{u^2z^2}\right)^{-n-1}du$$二項級数に展開します(一様収束性の議論は省略).$$f(z)=\frac{(z^2-1)^n}{z^{2n+1}}\sum_{m=0}^\infty\binom{n+1}{m}\frac{1}{z^{2m}}\int_1^\infty u^{-2n-2m-2}du$$積分を実行して\begin{equation}f(z)=\frac{1}{z}(1-z^{-2})^n\sum_{m=0}^\infty\binom{n+1}{m}\frac{z^{-2m}}{2n+2m+1}\tag{13}\end{equation}$(1-z^{-2})^n$ も展開します.\begin{equation}f(z)=\sum_{m=0}^\infty\sum_{k=0}^n\binom{n}{k}\binom{n+1}{m}\frac{(-1)^kz^{-2m-2k-1}}{2n+2m+1}\tag{14}\end{equation}これを $n$ 回微分すると\begin{equation}f^{(n)}(z)=\sum_{m=0}^\infty\sum_{k=0}^n\binom{n}{k}\binom{n+1}{m}\frac{(-1)^k(2m+2k+1)(2m+2k+2)\cdots(2m+2k+n)}{2n+2m+1}z^{-2m-2k-n-1}\tag{15}\end{equation}(15)は(11)の解です.これと,$Q_n(z)$ の超幾何関数による表示:\begin{equation}Q_n(z) = \frac{n!}{(2n+1)!!}\frac{1}{z^{n+1}}{}_2F_1\left[\begin{matrix}\frac{n+1}{2},\frac{n}{2}+1\\ n+\frac{3}{2}\end{matrix};\frac{1}{z^2}\right]\tag{16}\end{equation}を見比べてみましょう.(15)も(16)も,ともにルジャンドルの微分方程式(11)の特殊解であり,かつ $z=\infty$ での展開式($z^{-1}$ のべき展開)で $n+1$ 次からの級数になっています.なので $Q_n(z)$ と $f^{(n)}(z)$ は同じ特殊解であり,定数倍の差異しかないはずです.
ルジャンドルの微分方程式は $z=\pm1$,$\infty$ に確定特異点をもつフックス型微分方程式で,リーマンP記法で解全体を表現すると\begin{equation}P\left\{\begin{matrix}1 & \infty & -1\\0 & -n & 0\\0 & n+1 & 0\end{matrix}\;z\right\}\tag{17}\end{equation}これを見ると $z=\infty$ に属する指数は $-n$ と $n+1$ であり,いまは後者の級数解となっています.
したがって $z^{-n-1}$ の項を比較することによって$$f^{(n)}(z)=(-1)^n(2n-1)!!Q_n(z)$$以上から
$$Q_n(z)=\frac{(-1)^n}{(2n-1)!!}\frac{d^n}{dz^n}\left[(z^2-1)^n\int_z^\infty\frac{dt}{(t^2-1)^{n+1}}\right]$$
第1種ルジャンドル関数において示したラプラスの積分:\begin{equation}P_\nu(z)=\frac{1}{\pi}\int_0^\pi\left[z+(z^2-1)^{1/2}\cos\phi\right]^\nu d\phi\tag{18}\end{equation}の $Q_\nu$ バージョンを紹介します.
$\mathfrak{R}\nu>-1$ のときは\begin{equation}Q_\nu(z)=\frac{1}{2}\int_{-1}^1\frac{(1-t^2)^\nu}{2^\nu(z-t)^{\nu+1}}dt\tag{19}\end{equation}が成り立つのでした.ここで$$t=\frac{e^\t (z+1)^{1/2}-(z-1)^{1/2}}{e^\t (z+1)^{1/2}+(z-1)^{1/2}}$$なる置換を行うと
$\mathfrak{R}\nu>-1$, $$Q_\nu(z)=\int_0^{+\infty}\left[z+(z^2-1)^{1/2}\cosh\t\right]^{-\nu-1} d\t$$
(18)のcosがcoshになっている類似性に注目.
$\nu=n\in\ZZ_{>0}$ とします.また $|z|>1$ とします.実数 $w\in [-1,1]$ に対して\begin{align}\frac{1}{z-w} &=\frac{1}{z}\left(1-\frac{w}{z}\right)^{-1}\\&=\frac{1}{z}\sum_{m=0}^\infty\frac{w^m}{z^m}\end{align}これは $w$ の関数項級数として一様収束するので,以下のような計算ができます:\begin{equation}\int_{-1}^1 P_n(w)\frac{dw}{z-w} =\sum_{m=0}^\infty\frac{1}{z^{m+1}}\int_{-1}^1w^m P_n(w)dw\tag{20}\end{equation}右辺の積分はこちらの記事の(3)式と全く同じです.そこに計算方法が書いてありますので,ここでは結果のみを示すと,\begin{equation}\int_{-1}^1w^m P_n(w)dw =\left\{\begin{array}{cl}\dfrac{2^{n+1}m!(\frac{m+n}{2})!}{(m+n+1)!(\frac{m-n}{2})!}& (m\ge n\land m-n:\mathrm{even})\\0 & (\mathrm{else})\end{array}\right.\tag{21}\end{equation}(21)を(20)に適用します.$m=n$, $n+2$, $n+4$,$\cdots$ のみ和をとればよいので $m=n+2k$ として$$\int_{-1}^1 P_n(w)\frac{dw}{z-w} =\sum_{k=0}^\infty\frac{1}{z^{n+2k+1}}\frac{2^{n+1}(n+2k)!(n+k)!}{(2n+2k+1)!k!}$$ここで\begin{align}(n+2k)! &=n!\times (n+1)(n+3)\cdots(n+2k-1)\times (n+2)(n+4)\cdots(n+2k)\\ &=n!\: 2^{2k}\:\left(\frac{n+1}{2}\right)_k\left(\frac{n}{2}+1\right)_k \\(n+k)! &= n!\cdot (n+1)_k\\(2n+2k+1)! &=(2n+1)!\times (2n+2)(2n+4)\cdots(2n+2k)\times (2n+3)(2n+5)\cdots(2n+2k+1) \\ &=(2n+1)!\: 2^{2k}\: (n+1)_k \left(n+\frac{3}{2}\right)_k\end{align}を用いると\begin{equation}\int_{-1}^1 P_n(w)\frac{dw}{z-w} =\frac{2^{n+1}\: n!^2}{(2n+1)!}\frac{1}{z^{n+1}}\sum_{k=0}^\infty\frac{(\frac{n+1}{2})_k(\frac{n}{2}+1)_k}{(n+\frac{3}{2})_k k!}z^{-2k}\tag{22}\end{equation}(16)と比較して
$z\in\CC$ , $z$ は実軸の $[-1,1]$ にはないとする.$n\in\ZZ_{>0}$ とすると$$Q_n(z) =\frac{1}{2} \int_{-1}^1 P_n(w)\frac{dw}{z-w}$$
$|z|>1$ という仮定の下で定理4を導出しましたが,定理4の式を見ると $|z|\le 1$ でもよいことが分かります.もちろん実軸 $[-1,1]$ を除いて.
第5版です。いわずと知れた名著。特殊関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。