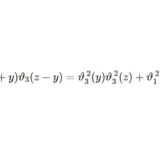前回はこちら:
もくじ
前々回ではテータ関数間の関係として次のような公式を得ました:\begin{align}\vartheta_2^{~4}+\vartheta_4^{~4}&=\vartheta_3^{~4}\tag{1}\\\vartheta_4^{~2}\vartheta_2(z)^2&=\vartheta_2^{~2}\vartheta_4(z)^2-\vartheta_3^{~2}\vartheta_1(z)^2\tag{2a}\\\vartheta_4^{~2}\vartheta_3(z)^2&=\vartheta_3^{~2}\vartheta_4(z)^2-\vartheta_2^{~2}\vartheta_1(z)^2\tag{2b}\\\vartheta_4^{~2}\vartheta_1(z)^2&=\vartheta_2^{~2}\vartheta_3(z)^2-\vartheta_3^{~2}\vartheta_2(z)^2\tag{2c}\\\vartheta_4^{~2}\vartheta_4(z)^2&=\vartheta_3^{~2}\vartheta_3(z)^2-\vartheta_2^{~2}\vartheta_2(z)^2\tag{2d}\end{align}(1)は(2d)で $z=0$ としたケースですので、上の5式は(2a)~(2d)の4式に集約されます。
ただ見方を変えてみると上の5式はすべてテータ関数を4つかけたものを1つの項としています。前回導いた加法定理の1つ:\begin{equation}\vartheta_4^{~2}\vartheta_1(z+y)\vartheta_1(z-y)=\vartheta_2^{~2}(y)\vartheta_3^{~2}(z)-\vartheta_3^{~2}(y)\vartheta_2^{~2}(z)\tag{3}\end{equation}これもテータ関数を4つかけて1つの項としています。 $y=0$ とすると(2c)となるのでさらなる一般化がなされたものといえます。
では、これ以上の一般化ができないものか。実はもっともっと基本的な関係式があって、(3)ですらその特殊ケースに過ぎないと。そのようなものを見つけるべく今回は解説していきます。
4個の独立変数 $w,x,y,z$ を考えます。この変数の組に対して次の変換を定めます。\begin{align}\begin{split}2w' &=-w+x+y+z\\2x' &=w-x+y+z\\2y' &=w+x-y+z\\2z' &=w+x+y-z\end{split}\tag{4}\end{align}基本的な行列の計算をすれば逆変換もまた同じ形をしています。すなわち\begin{align}\begin{split}2w &=-w'+x'+y'+z'\\2x &=w'-x'+y'+z'\\2y &=w'+x'-y'+z'\\2z &=w'+x'+y'-z'\end{split}\tag{5}\end{align}また(4)より\begin{equation}w+x+y+z=w'+x'+y'+z'\tag{6}\end{equation}が導かれます。
ここで新たな記法を導入します。$r=1,2,3,4$ として\begin{align}\begin{split}[r] & :=\vartheta_r(w)\vartheta_r(x)\vartheta_r(y)\vartheta_r(z)\\[1em] [r]' & :=\vartheta_r(w')\vartheta_r(x')\vartheta_r(y')\vartheta_r(z')\end{split}\tag{7}\end{align}と定義しましょう。テータ関数の添え字を全部同じにして4個かけています。違う添え字が混ざるバージョンもありますが、まずはここから。
$[r]$ は変数として $w,x,y,z$ を持ちます。また(4)の変換式より $[r]'$ もまた $w,x,y,z$ を変数として持ちます。
まずは $[r]$ や $[r]'$ を $z$ のみの関数として $w,x,y$ は定数とみなします。よって今は $[3](z)$ のように書いて $z$ の関数であることを明記しておきます。テータ関数の周期性を思い起こすと\begin{align}\begin{split}\vartheta_1(z+1) &=-\vartheta_1(z)\\\vartheta_1(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_1(z)\\\vartheta_2(z+1) &=-\vartheta_2(z)\\\vartheta_2(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_2(z)\\\vartheta_3(z+1) &=\vartheta_3(z)\\\vartheta_3(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_3(z)\\\vartheta_4(z+1) &=\vartheta_4(z)\\\vartheta_4(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_4(z)\end{split}\tag{8}\end{align}なので、例えば$$[3](z+1)=[3](z)\;,\;[3](z+\tau)=q^{-1}e^{-2\pi iz}[3](z)$$のように $[3]$ の(擬)周期性が確認できます。
このように $z$ を $+1$ あるいは $+\tau$ 増加させたときに $[1]'$ はどうなるでしょうか?
$z$ を $z+1$ にすると(4)の変換により $w',x',y'$ はそれぞれ $1/2$ ずつ増加し、$z'$ は $1/2$ 減ります。そこでテータ関数の半周期に関する公式:\begin{align}\begin{split}\vartheta_1\left(z+\frac{1}{2}\right) &=\vartheta_2(z)\\\vartheta_1\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_4(z)\\\vartheta_2\left(z+\frac{1}{2}\right) &=-\vartheta_1(z)\\\vartheta_2\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_3(z)\\\vartheta_3\left(z+\frac{1}{2}\right) &=\vartheta_4(z)\\\vartheta_3\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_2(z)\\\vartheta_4\left(z+\frac{1}{2}\right) &=\vartheta_3(z)\\\vartheta_4\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_1(z)\end{split}\tag{9}\end{align}を使います。つまり\begin{align}[1]'(z+1) &=\vartheta_1\left(w'+\frac{1}{2}\right)\vartheta_1\left(x'+\frac{1}{2}\right)\vartheta_1\left(y'+\frac{1}{2}\right)\vartheta_1\left(z'-\frac{1}{2}\right)\\&=\vartheta_2(w')\vartheta_2(x')\vartheta_2(y')\bigl(-\vartheta_2(z'\bigr))\\&=-[2]'(z)\end{align}同様に $z$ を $z+\tau$ とした場合は\begin{align}[1]'(z+\tau) &=\vartheta_1\left(w'+\frac{\tau}{2}\right)\vartheta_1\left(x'+\frac{\tau}{2}\right)\vartheta_1\left(y'+\frac{\tau}{2}\right)\vartheta_1\left(z'-\frac{\tau}{2}\right)\\&=-q^{-1}e^{-\pi i(w'+x'+y'-z')}\vartheta_4(w')\vartheta_4(x')\vartheta_4(y')\vartheta_4(z')\\&=-q^{-1}e^{-2\pi iz}[4]'(z)\end{align}このように調べていくと
| $z$の操作 | $[1]$ | $[2]$ | $[3]$ | $[4]$ | $[1]'$ | $[2]'$ | $[3]'$ | $[4]'$ |
| $+1$ | $-[1]$ | $-[2]$ | $[3]$ | $[4]$ | $-[2]'$ | $-[1]'$ | $[4]'$ | $[3]'$ |
| $+\tau$ | $-\lambda[1]$ | $\lambda[2]$ | $\lambda[3]$ | $-\lambda[4]$ | $-\lambda[4]'$ | $\lambda[3]'$ | $\lambda[2]'$ | $-\lambda[1]'$ |
ただし $\lambda=q^{-1}e^{-2\pi iz}$ です。
表1を見て例えば\begin{equation}F(z):=\frac{-[1]'+[2]'+[3]'+[4]'}{[3]}\tag{10}\end{equation}を定義すると $F(z)$ は二重周期 $1,\tau$ を持ち、高々1位の極をもちます(しかし1位の極が1つはありえないので極をもたないことになる)。よって $F(z)$ は $z$ によらない定数関数です。対称性から $w,x,y$ についても同じことが言えるので、(10)は $w,x,y,z$ によらない定数 $A$ となります:$$A\;[3] =-[1]'+[2]'+[3]'+[4]'$$$w=x=y=z=0$ とすると $w'=x'=y'=z'=0$ なので\begin{align}A\vartheta_3^{~4} &= -\vartheta_1^{~4}+\vartheta_2^{~4}+\vartheta_3^{~4}+\vartheta_4^{~4}\\&=\vartheta_2^{~4}+\vartheta_3^{~4}+\vartheta_4^{~4}\end{align}(1)より $A=2$ です。以上より\begin{equation}2\:[3] =-[1]'+[2]'+[3]'+[4]'\tag{11}\end{equation}これをあえて書き下すと\begin{align}\begin{split}2\vartheta_3(w)\vartheta_3(x)\vartheta_3(y)\vartheta_3(z) =&-\vartheta_1(w')\vartheta_1(x')\vartheta_1(y')\vartheta_1(z')\\&+ \vartheta_2(w')\vartheta_2(x')\vartheta_2(y')\vartheta_2(z')\\&+ \vartheta_3(w')\vartheta_3(x')\vartheta_3(y')\vartheta_3(z')\\&+ \vartheta_4(w')\vartheta_4(x')\vartheta_4(y')\vartheta_4(z')\end{split}\tag{12}\end{align}です。4つのテータ関数の積を1つの項として、5項間で成り立つ等式ができました。
(11)において $w,x,y,z$ をすべて $+1/2$ しましょう。(4)より $w',x',y',z'$ も $+1/2$ されますので \begin{equation}2\:[4] =[1]'-[2]'+[3]'+[4]'\tag{13}\end{equation}(11)において $w,x,y,z$ をすべて $+\tau/2$すると\begin{equation}2\:[2] =[1]'+[2]'+[3]'-[4]'\tag{14}\end{equation}(13)において $w,x,y,z$ をすべて $+\tau/2$ すると((11)で $+\frac{1+\tau}{2}$ するのと同じ)\begin{equation}2\:[1] =[1]'+[2]'-[3]'+[4]'\tag{15}\end{equation}以上をまとめて
\begin{align}2\:[1] &=[1]'+[2]'-[3]'+[4]'\\[1em] 2\:[2] &=[1]'+[2]'+[3]'-[4]'\\[1em] 2\:[3] &=-[1]'+[2]'+[3]'+[4]'\\[1em] 2\:[4] &=[1]'-[2]'+[3]'+[4]'\end{align}
定理1では4個のテータ関数の積をとる際に、すべて同じ添え字のものをかけています。そうでないバージョン、例えば$$[1234]:=\vartheta_1(w)\vartheta_2(x)\vartheta_3(y)\vartheta_4(z)$$のような項が現れるケースについては次回以降で見ていきましょう。
定理1のような式がそのまま役立つこともあるかもしれませんが、かなりややこしいので特殊な場合に成り立つ式を導出してみましょう。すべてやるのは大変なので定理1の第3式すなわち(12)で表される式に限定します。
4乗の関係式
$w=x=y=z$ とすると$w'=x'=$$y'=z'=z$ となるので\begin{equation}\vartheta_1^{~4}(z)+\vartheta_3^{~4}(z)=\vartheta_2^{~4}(z)+\vartheta_4^{~4}(z)\tag{16}\end{equation}これは有用そうな式です。(16)で $z=0$ なら\begin{equation}\vartheta_3^{~4}=\vartheta_2^{~4}+\vartheta_4^{~4}\tag{17}\end{equation}であり、すでに導出済みのものです。
2倍公式
次に $w=x=y=0$ として、$z$ を $2z$ とすると$$2\vartheta_3^{~3}\vartheta_3(2z)=\vartheta_1^{~4}(z)+\vartheta_2^{~4}(z)+\vartheta_3^{~4}(z)+\vartheta_4^{~4}(z)$$(16)を用いると\begin{align}\begin{split}\vartheta_3^{~3}\vartheta_3(2z) &=\vartheta_1^{~4}(z)+\vartheta_3^{~4}(z)\\[1em] &=\vartheta_2^{~4}(z)+\vartheta_4^{~4}(z) \end{split}\tag{18}\end{align}(18)は「2倍公式」の1つが得られました。
2乗の関係式
$w=x=0$ , $y=z$ とおくと $w'=x'=z$ , $y'=z'=0$ となるので\begin{equation}\vartheta_3^{~2}\vartheta_3^{~2}(z)=\vartheta_2^{~2}\vartheta_2^{~2}(z)+\vartheta_4^{~2}\vartheta_4^{~2}(z)\tag{19}\end{equation}(19)は過去に導出済みです(冒頭の(2d)式)。
2乗の関係式の一般形
$w=y$ , $x=z$ とおくと $w'=y'=z$ , $x'=z'=y$ となり\begin{equation}\vartheta_1^{~2}(y)\vartheta_1^{~2}(z)+\vartheta_3^{~2}(y)\vartheta_3^{~2}(z)=\vartheta_2^{~2}(y)\vartheta_2^{~2}(z)+\vartheta_4^{~2}(y)\vartheta_4^{~2}(z)\tag{20}\end{equation}(20)は(19)を一般化したものです。
加法定理
$w=x=0$ として $y$ を $z+y$ , $z$ を $z-y$ とおけば $w'=x'=z$ , $y'=-y$ , $z'=y$ となりますので$$2\vartheta_3^{~2}\vartheta_3(z+y)\vartheta_3(z-y)=\vartheta_1^{~2}(z)\vartheta_1^{~2}(y)+\vartheta_2^{~2}(z)\vartheta_2^{~2}(y)+\vartheta_3^{~2}(z)\vartheta_3^{~2}(y)+\vartheta_4^{~2}(z)\vartheta_4^{~2}(y)$$(20)を用いて\begin{align}\begin{split}\vartheta_3(z+y)\vartheta_3(z-y)\vartheta_3^2 &= \vartheta_1^2(z)\vartheta_1^2(y)+\vartheta_3^2(z)\vartheta_3^2(y) \\[1em] &= \vartheta_2^2(z)\vartheta_2^2(y)+\vartheta_4^2(z)\vartheta_4^2(y) \end{split}\tag{21}\end{align}(21)は前回ですでに紹介した式です。また(21)で $y=z$ とすると(18)を得ます。
定理1を起点としてさまざまな関係式が得られることが分かりました。上では定理1の第3式を例に導出していきましたが、定理1の他の3式でも同様の方針で議論できます。
4乗の関係式\begin{equation}\vartheta_1^{~4}(z)+\vartheta_3^{~4}(z)=\vartheta_2^{~4}(z)+\vartheta_4^{~4}(z)\tag{22}\end{equation}2倍公式\begin{align}\begin{split}\vartheta_2^{~3}\vartheta_2(2z) &=\vartheta_2^{~4}(z)-\vartheta_1^{~4}(z)\\ &=\vartheta_3^{~4}(z)-\vartheta_4^{~4}(z) \end{split}\tag{23}\\\begin{split}\vartheta_3^{~3}\vartheta_3(2z) &=\vartheta_1^{~4}(z)+\vartheta_3^{~4}(z)\\&=\vartheta_2^{~4}(z)+\vartheta_4^{~4}(z) \end{split}\tag{24}\\\begin{split}\vartheta_4^{~3}\vartheta_4(2z) &=\vartheta_4^{~4}(z)-\vartheta_1^{~4}(z)\\ &=\vartheta_3^{~4}(z)-\vartheta_2^{~4}(z) \end{split}\tag{25}\end{align}2乗の関係式\begin{equation}\vartheta_1^{~2}(y)\vartheta_1^{~2}(z)+\vartheta_3^{~2}(y)\vartheta_3^{~2}(z)=\vartheta_2^{~2}(y)\vartheta_2^{~2}(z)+\vartheta_4^{~2}(y)\vartheta_4^{~2}(z)\tag{26}\end{equation}加法定理\begin{align}\begin{split}\vartheta_2^2\vartheta_2(z+y)\vartheta_2(z-y) &= \vartheta_2^2(z)\vartheta_2^2(y)-\vartheta_1^2(z)\vartheta_1^2(y) \\ &= \vartheta_3^3(z)\vartheta_3^2(y)-\vartheta_4^2(z)\vartheta_4^2(y) \end{split}\tag{27}\\\begin{split}\vartheta_3^2\vartheta_3(z+y)\vartheta_3(z-y) &= \vartheta_1^2(z)\vartheta_1^2(y)+\vartheta_3^2(z)\vartheta_3^2(y) \\ &= \vartheta_2^2(z)\vartheta_2^2(y)+\vartheta_4^2(z)\vartheta_4^2(y) \end{split}\tag{28}\\\begin{split}\vartheta_4^2\vartheta_4(z+y)\vartheta_4(z-y) &= \vartheta_4^2(z)\vartheta_4^2(y)-\vartheta_1^2(z)\vartheta_1^2(y) \\ &= \vartheta_3^3(z)\vartheta_3^2(y)-\vartheta_2^2(z)\vartheta_2^2(y) \end{split}\tag{29}\end{align}
なお前回紹介したように、系2で示されていない形の加法定理もあります。次回もこのような話を続けます。
$\mu=q^{-4}e^{-4\pi iz}$ とするとき、次の擬周期性を示せ。
| $z$の操作 | $[1]$ | $[2]$ | $[3]$ | $[4]$ | $[1]'$ | $[2]'$ | $[3]'$ | $[4]'$ |
| $+2$ | $[1]$ | $[2]$ | $[3]$ | $[4]$ | $[1]'$ | $[2]'$ | $[3]'$ | $[4]'$ |
| $+2\tau$ | $\mu[1]$ | $\mu[2]$ | $\mu[3]$ | $\mu[4]$ | $\mu[1]'$ | $\mu[2]'$ | $\mu[3]'$ | $\mu[4]'$ |
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。