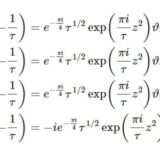前回は:
本シリーズ一覧は:
最初に便利な擬周期、半周期の式を復習しておきます。
\begin{align}\vartheta_1(z+1) &=-\vartheta_1(z)\\\vartheta_1(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_1(z)\\\vartheta_2(z+1) &=-\vartheta_2(z)\\\vartheta_2(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_2(z)\\\vartheta_3(z+1) &=\vartheta_3(z)\\\vartheta_3(z+\tau) &=q^{-1}e^{-2\pi iz}\vartheta_3(z)\\\vartheta_4(z+1) &=\vartheta_4(z)\\\vartheta_4(z+\tau) &=-q^{-1}e^{-2\pi iz}\vartheta_4(z)\end{align}\begin{align}\vartheta_1\left(z+\frac{1}{2}\right) &=\vartheta_2(z)\\\vartheta_1\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_4(z)\\\vartheta_2\left(z+\frac{1}{2}\right) &=-\vartheta_1(z)\\\vartheta_2\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_3(z)\\\vartheta_3\left(z+\frac{1}{2}\right) &=\vartheta_4(z)\\\vartheta_3\left(z+\frac{\tau}{2}\right) &=q^{-\frac{1}{4}}e^{-\pi iz}\vartheta_2(z)\\\vartheta_4\left(z+\frac{1}{2}\right) &=\vartheta_3(z)\\\vartheta_4\left(z+\frac{\tau}{2}\right) &=iq^{-\frac{1}{4}}e^{-\pi iz}\vartheta_1(z)\end{align}
さてさて、\begin{equation}f(z):=\frac{\vartheta_3(z,\tau)\vartheta_4(z,\tau)}{\vartheta_4(2z,2\tau)}\tag{1}\end{equation}なる関数 $f(z)$ を用意します。このとき定理0を使って周期性を確認すると\begin{align}f\left(z+\frac{1}{2}\right) &=f(z)\\[1em] f(z+\tau) &=\frac{-e^{-2\pi i\tau}e^{-4\pi iz}\vartheta_3(z,\tau)\vartheta_4(z,\tau)}{-e^{-2\pi i\tau}e^{-4\pi iz}\vartheta_4(2z,2\tau)}=f(z)\end{align}です。なので $f(z)$ は二重周期をもつ有理型関数となります。
次に $f(z)$ の極と零点を調べます。4つのテータ関数 $\vartheta_1(z)$,$\vartheta_2(z)$,$\vartheta_3(z)$,$\vartheta_4(z)$ は極をもたない整関数であり、零点はそれぞれ $0$,$\frac{1}{2}$,$\frac{1+\tau}{2}$,$\frac{\tau}{2}$ (および合同な点)でしたから $f(z)$ の分子の零点は $\frac{1+\tau}{2}$ と $\frac{\tau}{2}$ および合同な点です。すなわち$$z=\frac{1+\tau}{2}+m+n\tau\;,\; \frac{\tau}{2}+m+n\tau\quad(m,n\in\ZZ)$$ですが、これは$$z=\frac{m}{2}+\left(n+\frac{1}{2}\right)\tau\quad(m,n\in\ZZ)$$とまとめて書くことができます。一方 $f(z)$ の分母の零点は、周期が $1,2\tau$ であることに注意して$$2z=\tau+m+2n\tau\quad(m,n\in\ZZ)$$$$\therefore\quad z=\frac{m}{2}+\left(n+\frac{1}{2}\right)\tau\quad(m,n\in\ZZ)$$以上から $f(z)$ の分母と分子は同一の零点をもつために相殺し、結局のところ $f(z)$ は極も零点ももたないことになります。
$f(z)$ は極をもたない二重周期関数ということになり、そのようなものは定数関数に限るのでした。$z\to 0$ によってその定数は定まり、結局$$\frac{\vartheta_3(z,\tau)\vartheta_4(z,\tau)}{\vartheta_4(2z,2\tau)}=\frac{\vartheta_3(\tau)\vartheta_4(\tau)}{\vartheta_4(2\tau)}$$ただし $z=0$ としたテータ定数 $\vartheta_j(0,\tau)$ を $\vartheta_j(\tau)$ と表記しています。 さらに $z\to z+\frac{\tau}{2}$ として$$\frac{\vartheta_1(z,\tau)\vartheta_2(z,\tau)}{\vartheta_1(2z,2\tau)}=\frac{\vartheta_3(\tau)\vartheta_4(\tau)}{\vartheta_4(2\tau)}$$を得ます。まとめると
$$\frac{\vartheta_3(z,\tau)\vartheta_4(z,\tau)}{\vartheta_4(2z,2\tau)}=\frac{\vartheta_3(\tau)\vartheta_4(\tau)}{\vartheta_4(2\tau)}$$$$\frac{\vartheta_1(z,\tau)\vartheta_2(z,\tau)}{\vartheta_1(2z,2\tau)}=\frac{\vartheta_3(\tau)\vartheta_4(\tau)}{\vartheta_4(2\tau)}$$
極と周期性から導く
\begin{equation}\phi(z):=\frac{\vartheta_1'(z)\vartheta_4(z)-\vartheta_1(z)\vartheta_4'(z)}{\vartheta_2(z)\vartheta_3(z)}\tag{2}\end{equation}を定義します。定理0を使うと$$\phi(z+1)=\phi(z+\tau)=\phi(z)$$であることが確かめられるので $\phi(z)$ は二重周期をもちます。
$\phi(z)$ は極をもつでしょうか?テータ関数は整関数なので、(2)の右辺の分子からは極が生ずることはありません。分母をみると $\phi(z)$ の極たりえるのは $\vartheta_2(z)$ , $\vartheta_3(z)$ の零点すなわち\begin{equation}z\equiv\frac{1}{2}\;,\; \frac{1+\tau}{2}\quad (\mathrm{mod}\; 1,\tau)\tag{3}\end{equation}です。
というわけで(3)を満たす $z$ は $\phi(z)$ の極である可能性があります。しかし実は、(2)の分子も同じ零点をもつためにすべて相殺されてしまうのです。確認してみましょう。こちらの定理3と4より\begin{align}\vartheta_1' &=\pi\vartheta_2\vartheta_3\vartheta_4\tag{4a}\\\vartheta_2' &= 0\tag{4b}\\\vartheta_3' &= 0\tag{4c}\\\vartheta_4' &= 0\tag{4d}\end{align}であることを念頭に置きつつ、定理0より $\vartheta_4'(1/2)=0$ , $\vartheta_1'(1/2)=0$ となります。よって(2)の分子は $z\equiv 1/2$ を零点にもちます。これが分母の同じ零点を打ち消すため、$\phi(z)$ は $z\equiv1/2$ を零点としてもたないことになります。ではもう一方の点 $z\equiv\frac{1+\tau}{2}$ はどうでしょう。定理0と(4a)~(4d)を必要に応じて使って\begin{align}\vartheta_1'\left(\frac{1+\tau}{2}\right) &=-\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_3\tag{5a}\\\vartheta_2'\left(\frac{1+\tau}{2}\right) &=-\pi e^{-\frac{1}{4}\pi i\tau}\vartheta_4\tag{5b}\\\vartheta_3'\left(\frac{1+\tau}{2}\right) &=\pi i e^{-\frac{1}{4}\pi i\tau}\vartheta_2\vartheta_3\vartheta_4\tag{5c}\\\vartheta_4'\left(\frac{1+\tau}{2}\right) &=-\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_2\tag{5d}\end{align}なので$$\vartheta_1'\left(\frac{1+\tau}{2}\right)\vartheta_4\left(\frac{1+\tau}{2}\right)-\vartheta_1\left(\frac{1+\tau}{2}\right)\vartheta_4'\left(\frac{1+\tau}{2}\right)=0$$を得ます。よってこの点も $\phi(z)$ の極になりません。
結局 $\phi(z)$ は極をもたない二重周期関数になりますが、そのようなものは定数関数に限ります。$$\frac{\vartheta_1'(z)\vartheta_4(z)-\vartheta_1(z)\vartheta_4'(z)}{\vartheta_2(z)\vartheta_3(z)}=A$$$z\to 0$ として$$A=\frac{\vartheta_4\vartheta'_1}{\vartheta_2\vartheta_3}=\pi\vartheta_4^{~2}$$最後の変形は(4a)を使いました。したがって\begin{equation}\frac{\vartheta_1'(z)\vartheta_4(z)-\vartheta_1(z)\vartheta_4'(z)}{\vartheta_2(z)\vartheta_3(z)}=\pi\vartheta_4^{~2}\tag{6}\end{equation}簡単な微分の知識から\begin{equation}\frac{d}{dz}\left(\frac{\vartheta_1(z)}{\vartheta_4(z)}\right)=\pi\vartheta_4^{~2}\frac{\vartheta_2(z)\vartheta_3(z)}{\vartheta_4^{~2}(z)}\tag{7}\end{equation}なる関係を得られます。
2つめの方程式
まったく同様の方法で(7)と類似の等式を得られます。$$\frac{\vartheta_2'(z)\vartheta_4(z)-\vartheta_2(z)\vartheta_4'(z)}{\vartheta_1(z)\vartheta_3(z)}$$なる関数は二重周期 $1,\tau$ をもち、極をもちません。よって定数関数であり、$$\frac{\vartheta_2'(z)\vartheta_4(z)-\vartheta_2(z)\vartheta_4'(z)}{\vartheta_1(z)\vartheta_3(z)}=B$$$z\to 1/2$ としましょう。定数値\begin{align}\vartheta_1'(1/2) &=0\tag{8a}\\\vartheta_2'(1/2) &= -\pi\vartheta_2\vartheta_3\vartheta_4\tag{8b}\\\vartheta_3'(1/2) &= 0\tag{8c}\\\vartheta_4'(1/2) &= 0\tag{8d}\end{align}を踏まえて$$B=-\pi\vartheta_3^{~2}$$となります。したがって\begin{equation}\frac{d}{dz}\left(\frac{\vartheta_2(z)}{\vartheta_4(z)}\right)=-\pi\vartheta_3^{~2}\frac{\vartheta_1(z)\vartheta_3(z)}{\vartheta_4^{~2}(z)}\tag{9}\end{equation}
3つめの方程式
まったく同様にして3つめの式を導出します。$$\frac{\vartheta_3'(z)\vartheta_4(z)-\vartheta_3(z)\vartheta_4'(z)}{\vartheta_1(z)\vartheta_2(z)}$$なる関数は二重周期 $1,\tau$ をもち、極をもちません。よって定数関数であり、$$\frac{\vartheta_3'(z)\vartheta_4(z)-\vartheta_3(z)\vartheta_4'(z)}{\vartheta_1(z)\vartheta_2(z)}=C$$$z\to \tau/2$ とすると、下の方に記載した公式(91)以降も活用して$$C=-\pi\vartheta_2^{~2}$$ と求まります。最終結果は下記の定理2に記載しておきます。
まとめたものが次です。ヤコビの楕円関数へとつながっていきます。
\begin{align}\frac{d}{dz}\left(\frac{\vartheta_1(z)}{\vartheta_4(z)}\right)&=\pi\vartheta_4^{~2}\frac{\vartheta_2(z)\vartheta_3(z)}{\vartheta_4^{~2}(z)}\\\frac{d}{dz}\left(\frac{\vartheta_2(z)}{\vartheta_4(z)}\right)&=-\pi\vartheta_3^{~2}\frac{\vartheta_1(z)\vartheta_3(z)}{\vartheta_4^{~2}(z)}\\\frac{d}{dz}\left(\frac{\vartheta_3(z)}{\vartheta_4(z)}\right)&=-\pi\vartheta_2^{~2}\frac{\vartheta_1(z)\vartheta_2(z)}{\vartheta_4^{~2}(z)}\end{align}
今後も使うかもしれないですし、がんばって計算したのでメモしておきます。\begin{align}\vartheta_1 &=0\tag{90}\\[1em] \vartheta_1(1/2) &=\vartheta_2\tag{91a}\\\vartheta_2(1/2) &=0\tag{91b}\\\vartheta_3(1/2) &=\vartheta_4\tag{91c}\\\vartheta_4(1/2) &=\vartheta_3\tag{91d}\\[1em] \vartheta_1\left(\frac{1+\tau}{2}\right) &=e^{-\frac{1}{4}\pi i\tau}\vartheta_3\tag{92a}\\\vartheta_2\left(\frac{1+\tau}{2}\right) &=-ie^{-\frac{1}{4}\pi i\tau}\vartheta_4\tag{92b}\\\vartheta_3\left(\frac{1+\tau}{2}\right) &=0\tag{92c}\\\vartheta_4\left(\frac{1+\tau}{2}\right) &=e^{-\frac{1}{4}\pi i\tau}\vartheta_2\tag{92d}\\[1em] \vartheta_1\left(\frac{\tau}{2}\right) &=ie^{-\frac{1}{4}\pi i\tau}\vartheta_4\tag{93a}\\\vartheta_2\left(\frac{\tau}{2}\right) &=e^{-\frac{1}{4}\pi i\tau}\vartheta_3\tag{93b}\\\vartheta_3\left(\frac{\tau}{2}\right) &=e^{-\frac{1}{4}\pi i\tau}\vartheta_2\tag{93c}\\\vartheta_4\left(\frac{\tau}{2}\right) &=0\tag{93d}\\[1em] \vartheta'_1 &=\pi\vartheta_2\vartheta_3\vartheta_4\tag{94a}\\\vartheta'_2 &=0\tag{94b}\\\vartheta'_3 &=0\tag{94c}\\\vartheta'_4 &=0\tag{94d}\\[1em] \vartheta'_1(1/2) &=0\tag{95a}\\\vartheta'_2(1/2) &=-\pi\vartheta_2\vartheta_3\vartheta_4\tag{95b}\\\vartheta'_3(1/2) &=0\tag{95c}\\\vartheta'_4(1/2) &=0\tag{95d}\\[1em] \vartheta'_1\left(\frac{1+\tau}{2}\right) &=-\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_3\tag{96a}\\\vartheta'_2\left(\frac{1+\tau}{2}\right) &=-\pi e^{-\frac{1}{4}\pi i\tau}\vartheta_4\tag{96b}\\\vartheta'_3\left(\frac{1+\tau}{2}\right) &=\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_2\vartheta_3\vartheta_4\tag{96c}\\\vartheta'_4\left(\frac{1+\tau}{2}\right) &=-\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_2\tag{96d}\\[1em] \vartheta'_1\left(\frac{\tau}{2}\right) &=\pi e^{-\frac{1}{4}\pi i\tau}\vartheta_4\tag{97a}\\\vartheta'_2\left(\frac{\tau}{2}\right) &=-\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_3\tag{97b}\\\vartheta'_3\left(\frac{\tau}{2}\right) &=-\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_2\tag{97c}\\\vartheta'_4\left(\frac{\tau}{2}\right) &=\pi ie^{-\frac{1}{4}\pi i\tau}\vartheta_2\vartheta_3\vartheta_4\tag{97d}\end{align}
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。