球座標系のヘルムホルツ方程式と球ベッセル関数

これまで物理に現れるいくつかの３次元の微分方程式を扱ってきました。そこでは極座標や円筒座標に変換することでベッセルの微分方程式やルジャンドルの陪微分方程式といった、特殊な2階線型方程式が現れることを確認しました。今回は球ベッセル微分方程式が現れる「ヘルムホルツ方程式」の極座標表示に取り組みます。流れは以下の過去記事と類似していますので合わせて参考にしてください。

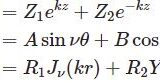2021年12月22日 【物理数学】円筒座標のラプラス方程式とベッセル関数

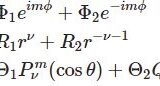2021年12月28日 球座標のラプラス方程式とルジャンドル陪微分方程式

まずは左辺のラプラシアンを球座標に変換する必要があります。

球座標への変換とラプラシアン

直交座標から球座標への変換は$$\begin{cases}x=r\sin\theta\cos\phi\\y=r\sin\theta\sin\phi\\z=r\cos\theta\end{cases}$$で与えられます。逆に解くと$$\begin{cases}r&=&\sqrt{x^2+y^2+z^2}\\\theta&=&\arccos\displaystyle\frac{z}{\sqrt{x^2+y^2+z^2}}\\\phi&=&\arctan\displaystyle\frac{y}{x}\end{cases}$$とあらわせます。

偏微分しましょう。$r,\theta,\phi$ をそれぞれ $x,y,z$ で偏微分するので９回やらねばなりません。偏微分したら $x,y,z$ の式になりますが、それを $r,\theta,\phi$ で表しておきます。$$\begin{cases}\displaystyle\frac{\partial r}{\partial x}&=&\sin\theta\cos\phi \\ \displaystyle\frac{\partial r}{\partial y}&=&\sin\theta\sin\phi \\ \displaystyle\frac{\partial r}{\partial z}&=&\cos\theta \\[1em] \displaystyle\frac{\partial \theta}{\partial x}&=&\displaystyle\frac{\cos\theta\cos\phi}{r} \\ \displaystyle\frac{\partial \theta}{\partial y}&=& \displaystyle\frac{\cos\theta\sin\phi}{r} \\ \displaystyle\frac{\partial \theta}{\partial z}&=& -\displaystyle\frac{\sin\theta}{r} \\[1em] \displaystyle\frac{\partial \phi}{\partial x}&=& -\displaystyle\frac{\sin\phi}{r\sin\theta} \\ \displaystyle\frac{\partial \phi}{\partial y}&=& \displaystyle\frac{\cos\phi}{r\sin\theta} \\ \displaystyle\frac{\partial \phi}{\partial z}&=& 0\end{cases}$$

チェインルールにより微分演算子の変換は以下のようになります。$$\begin{cases} \displaystyle\frac{\partial}{\partial x}&=&\sin\theta\cos\phi \displaystyle\frac{\partial}{\partial r}+\frac{\cos\theta\cos\phi}{r}\frac{\partial}{\partial \theta}-\frac{\sin\phi}{r\sin\theta}\frac{\partial}{\partial \phi} \\ \displaystyle\frac{\partial}{\partial y}&=&\sin\theta\sin\phi \displaystyle\frac{\partial}{\partial r}+\frac{\cos\theta\sin\phi}{r}\frac{\partial}{\partial \theta}+\frac{\cos\phi}{r\sin\theta}\frac{\partial}{\partial \phi} \\ \displaystyle\frac{\partial}{\partial z}&=&\cos\theta \displaystyle \frac{\partial}{\partial r}-\frac{\sin\theta}{r}\frac{\partial}{\partial \theta} \end{cases}$$

よってラプラシアンは\begin{eqnarray*}\Delta u&=& \frac{\partial^2 u}{\partial x^2}+ \frac{\partial^2 u}{\partial y^2}+ \frac{\partial^2 u}{\partial z^2} \\ &=& \left(\sin\theta\cos\phi \displaystyle\frac{\partial}{\partial r}+\frac{\cos\theta\cos\phi}{r}\frac{\partial}{\partial \theta}-\frac{\sin\phi}{r\sin\theta}\frac{\partial}{\partial \phi}\right) \left(\sin\theta\cos\phi \displaystyle\frac{\partial u}{\partial r}+\frac{\cos\theta\cos\phi}{r}\frac{\partial u}{\partial \theta}-\frac{\sin\phi}{r\sin\theta}\frac{\partial u}{\partial \phi}\right) \\ &&+\left( \sin\theta\sin\phi \displaystyle\frac{\partial}{\partial r}+\frac{\cos\theta\sin\phi}{r}\frac{\partial}{\partial \theta}+\frac{\cos\phi}{r\sin\theta}\frac{\partial}{\partial \phi} \right) \left( \sin\theta\sin\phi \displaystyle\frac{\partial u}{\partial r}+\frac{\cos\theta\sin\phi}{r}\frac{\partial u}{\partial \theta}+\frac{\cos\phi}{r\sin\theta}\frac{\partial u}{\partial \phi} \right) \\ &&+ \left(\cos\theta \displaystyle \frac{\partial}{\partial r}-\frac{\sin\theta}{r}\frac{\partial}{\partial \theta} \right) \left(\cos\theta \displaystyle \frac{\partial u}{\partial r}-\frac{\sin\theta}{r}\frac{\partial u}{\partial \theta} \right) \\&=& \frac{1}{r^2} \frac{\partial }{\partial r}\left(r^2 \frac{\partial u}{\partial r} \right) +\frac{1}{r^2\sin\theta} \frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial u}{\partial \theta} \right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2 u}{\partial\phi^2} \end{eqnarray*}

ラプラス方程式の解法

方程式を変数分離によって解いていきます。もちろんそこで得られる解 $u$ は変数分離可能という前提を満たすもののみとなります。

ステップ１：$\phi$ の分離

ヘルムホルツ方程式 $(\Delta+k^2) u=0$ を球座標で表すと$$ \frac{1}{r^2} \frac{\partial }{\partial r}\left(r^2 \frac{\partial u}{\partial r} \right) +\frac{1}{r^2\sin\theta} \frac{\partial }{\partial \theta}\left(\sin\theta\frac{\partial u}{\partial \theta} \right)+\frac{1}{r^2\sin^2\theta}\frac{\partial^2 u}{\partial\phi^2}+k^2u =0$$ この方程式を解くために$$u(r,\theta,\phi)=R(r)\Theta(\theta)\Phi(\phi)$$と変数分離します。$$ \frac{\Theta\Phi}{r^2} \frac{d }{dr}\left(r^2 \frac{dR}{dr}\right) +\frac{R\Phi}{r^2\sin\theta} \frac{d}{d\theta}\left(\sin\theta\frac{d\Theta}{d\theta} \right)+\frac{R\Theta}{r^2\sin^2\theta}\frac{d^2 \Phi}{d\phi^2} +k^2R\Theta\Phi=0$$両辺に $r^2\sin^2\theta $ をかけて $R\Theta\Phi$ で割ります。整理すると$$\frac{\sin^2\theta}{R}\frac{d }{dr}\left(r^2 \frac{dR}{dr}\right) +\frac{\sin\theta}{\Theta}\frac{d}{d\theta}\left(\sin\theta\frac{d\Theta}{d\theta} \right)+k^2r^2\sin^2\theta=-\frac{1}{\Phi}\frac{d^2 \Phi}{d\phi^2}\tag{1}$$この左辺は $r,\theta$ の関数、右辺は $\phi$ の関数です。よって任意の $r,\theta,\phi$ で式が成り立つためには左辺および右辺が定数でなければいけません。この定数を $m^2$ とおくと右辺は$$ \frac{d^2 \Phi}{d\phi^2} =-m^2\Phi(\phi)$$よって $\phi$ のみに関する微分方程式が得られ、その解は一般に$$\Phi(\phi)=\Phi_1e^{im\phi}+ \Phi_2e^{-im\phi}\;(m,\Phi_1,\Phi_2\in\mathbb{C})$$と表されます。

ステップ２：$r$ の分離と球ベッセル微分方程式

(1)の左辺は$$ \frac{\sin^2\theta}{R}\frac{d }{dr}\left(r^2 \frac{dR}{dr}\right) +\frac{\sin\theta}{\Theta}\frac{d}{d\theta}\left(\sin\theta\frac{d\Theta}{d\theta} \right)+k^2r^2\sin^2\theta= m^2$$これを変形して$$ \frac{1}{R}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+k^2r^2 =-\frac{1}{\Theta\sin\theta}\frac{d}{d\theta}\left(\sin\theta\frac{d\Theta}{d\theta}\right)+\frac{m^2}{\sin^2\theta}\tag{2}$$左辺は $r$ の関数、右辺は $\theta$ の関数です。よって任意の $r,\theta$ で式が成り立つためには左辺および右辺が定数でなければいけません。この定数を $\nu(\nu+1)$ とおくと左辺は$$ \frac{1}{R}\frac{d}{dr}\left(r^2\frac{dR}{dr}\right)+k^2r^2 = \nu(\nu+1)$$さらに変形すると$$\frac{d^2R}{dr^2}+\frac{2}{r}\frac{dR}{dr}+\left[k^2-\frac{\nu(\nu+1)}{r^2}\right]R=0$$$kr\equiv\rho$ と置換し$$\therefore\;\rho^2\frac{d^2R}{d\rho^2}+2\rho\frac{dR}{d\rho}+\left[\rho^2-\nu(\nu+1)\right]R=0$$これは球ベッセルの微分方程式とよばれる形です。この方程式の解は第1種球ベッセル関数 $j_\nu(\rho)$ と第2種球ベッセル関数 $n_\nu(\rho)$ の線型結合で表されます。この関数はその名の通りベッセル関数と深い関係があります（後述）。

ステップ３：$\theta$ の分離とルジャンドル陪微分方程式

(2)の右辺は$$-\frac{1}{\Theta\sin\theta}\frac{d}{d\theta}\left(\sin\theta\frac{d\Theta}{d\theta}\right)+\frac{m^2}{\sin^2\theta} =\nu(\nu+1)$$$$\therefore\; \frac{1}{\sin\theta}\frac{d}{d\theta}\left(\sin\theta\frac{d\Theta}{d\theta}\right)+\left[\nu(\nu+1)-\frac{m^2}{\sin^2\theta}\right]\Theta =0\tag{3}$$

$t=\cos\theta$ と置換すると$dt=-\sin\theta d\theta$ なので$$\frac{d}{d\theta}=\frac{dt}{d\theta}\frac{d}{dt}=-\sqrt{1-t^2}\frac{d}{dt}$$よって $$ \sin\theta\frac{d\Theta}{d\theta} =-(1-t^2)\frac{d\Theta}{dt}$$と書けるので(3)は$$\frac{d}{dt}\left\{(1-t^2)\frac{d\Theta}{dt}\right\}+\left[\nu(\nu+1)-\frac{m^2}{1-t^2}\right]\Theta=0$$これを「ルジャンドルの陪微分方程式」といい、その独立な$2$解は$$P_\nu^m(t)=\frac{1}{\Gamma(1-m)}\left(\frac{1+t}{1-t}\right)^\frac{m}{2}{}_2F_1\left(\begin{matrix}-\nu , \nu+1 \\ 1-m\end{matrix} ;\frac{1-t}{2}\right)$$$$Q_\nu^m(t)=\frac{\sqrt{\pi}\Gamma(m+\nu+1)}{2^{\nu+1}\Gamma(\nu+\frac{3}{2})}e^{i\pi m}\frac{(t^2-1)^{\frac{m}{2}}}{t^{m+\nu+1}}{}_2F_1\left(\begin{matrix}\frac{m+\nu+1}{2},\frac{m+\nu+2}{2} \\ \nu+\frac{3}{2}\end{matrix} ;\frac{1}{t^2}\right)$$です。$P_\nu^m$ , $Q_\nu^m$ はそれぞれ第1種ルジャンドル陪函数、第2種ルジャンドル陪函数といいます。どうしてこうなるかは省略します。いつか取り組んでみたいです。

球ベッセル微分方程式について

ステップ2の話に戻ります。関数 $R(\rho)$ を求めるには球ベッセルの微分方程式を解くことになります。一般的な話になるので変数を $x$ と $y(x)$ にしておきます。

ステップ１：$\nu=0$ の場合で慣れてみる

$\nu=0$ で試してみます。このとき微分方程式は$$x^2y^{\prime\prime}+2xy'+x^2y=0$$と表されます。フロベニウス法を使います。$$y=\sum_{n=0}^\infty a_nx^{n+r}\;,\; a_0\neq 0$$とおくと\begin{eqnarray*}y'&=&\sum_{n=0}^\infty (n+r)a_nx^{n+r-1}\\y^{\prime\prime}&=&\sum_{n=0}^\infty (n+r)(n+r-1)a_nx^{n+r-2}\end{eqnarray*}これらを微分方程式に代入すると $x^r$ の係数は $r(r+1)a_0=0$ となります。$a_0\neq 0$ でしたから $r=0,-1$ となります。２つの $r$ がそれぞれ解を作るのですが（それらが独立かどうかは議論が要ります）、今は $r=0$ のみでやります。

あらためて $$y=\sum_{n=0}^\infty a_nx^n\;,\; a_0\neq 0$$とおきます。微分方程式に代入すると$$2a_1x+ \sum_{n=0}^\infty \left[(n+2)(n+3)a_{n+2}+a_n\right]x^{n+2}=0$$$$\therefore\;\begin{cases}a_1 &=& 0 \\ a_{n+2}&=&\displaystyle\frac{-1}{(n+2)(n+3)}a_n\quad(n\ge 0)\end{cases}$$奇数項はすべてゼロとなりますね。よって $$\begin{cases}a_{2m-1} &=& 0 \\ a_{2m}&=&\displaystyle\frac{-1}{2m(2m+1)}a_{2m-2}\quad(m\ge 1)\end{cases}$$偶数項の漸化式を繰り返し用いれば\begin{eqnarray*}a_{2m}&=& \frac{-1}{2m(2m+1)}a_{2m-2} \\ &\vdots& \\ &=& \frac{(-1)^m}{(2m)!!(2m+1)!!}a_0 \quad(m\ge 0) \\ &=& \frac{\Gamma(\frac{3}{2})(-1)^m}{2^{2m}m!\Gamma(m+\frac{3}{2})}a_0 \\ &=& a_0\frac{\sqrt{\pi}}{2}\frac{(-1)^m}{2^{2m}m!\Gamma(m+\frac{3}{2})}\end{eqnarray*} よって $a_0=1$ ととると微分方程式の特殊解 $y_1(x)$ は\begin{eqnarray*} y_1(x)&=&\frac{\sqrt{\pi}}{2}\sum_{m=0}^\infty\frac{(-1)^m}{2^{2m}m!\Gamma(m+\frac{3}{2})}x^{2m}\\ &=&\sqrt{\frac{\pi}{2x}} \sum_{m=0}^\infty \frac{(-1)^m}{2^{2m+\frac{1}{2}}m!\Gamma(m+1+\frac{1}{2})}x^{2m+\frac{1}{2}}\\ &=& \sqrt{\frac{\pi}{2x}} J_{\frac{1}{2}}(x)\end{eqnarray*}ここで $$J_\nu(x)= \sum_{m=0}^\infty \frac{(-1)^m}{2^{2m+\nu}m!\Gamma(m+\nu+1)}x^{2m+\nu} $$ を第1種ベッセル関数といいます。そしてこの $y_1(x)$ を $\nu=0$ における第1種球ベッセル関数 $j_0(x)$ といいます。すなわち $$ j_0(x) = \sqrt{\frac{\pi}{2x}} J_{\frac{1}{2}}(x) $$が微分方程式の１つの特殊解というわけです。

ステップ２：一般の $\nu$ について

$$x^2y^{\prime\prime}+2xy'+\left[x^2-\nu(\nu+1)\right]y=0$$においてフロベニウス法を用います。$$y=\sum_{n=0}^\infty a_nx^{n+r}\;,\; a_0\neq 0$$とおくと\begin{eqnarray*}y'&=&\sum_{n=0}^\infty (n+r)a_nx^{n+r-1}\\y^{\prime\prime}&=&\sum_{n=0}^\infty (n+r)(n+r-1)a_nx^{n+r-2}\end{eqnarray*}これらを微分方程式に代入すると $x^r$ の係数は $(r-\nu)(r+\nu+1)a_0=0$ となります。$a_0\neq 0$ でしたから $r=\nu,-\nu-1$ となります。今は $r=\nu$ のみでやります。

あらためて $$y=\sum_{n=0}^\infty a_nx^{n+\nu}\;,\; a_0\neq 0$$とおきます。微分方程式に代入すると$$2(\nu+1)a_1x+ \sum_{n=2}^\infty \left[n(n+2\nu+1)a_n+a_{n-2}\right]x^n=0$$$$\therefore\;\begin{cases}a_1 &=& 0 \\ a_{n}&=&\displaystyle\frac{-1}{n(n+2\nu+1)}a_{n-2}\end{cases}$$奇数項はすべてゼロとなります。 よって$$\begin{cases}a_{2m-1} &=& 0 \\ a_{2m}&=&\displaystyle\frac{-1}{2m(2m+2\nu+1)}a_{2m-2}\quad(m\ge 1)\end{cases}$$偶数項の漸化式を繰り返し用いれば \begin{eqnarray*}a_{2m}&=& \frac{-1}{2m(2m+1)}a_{2m-2} \\ &\vdots& \\ &=& \frac{(-1)^m}{(2m)!!\cdot (2m+2\nu+1)(2m+2\nu-1)\cdots(2\nu+3)}a_0 \quad(m\ge 1) \\ &=& \frac{(-1)^m}{2^{2m}m!\cdot (m+\nu+\frac{1}{2})(m+\nu-\frac{1}{2})\cdots(\nu+\frac{3}{2})}a_0 \\&=& a_0\frac{(-1)^m\Gamma(\nu+\frac{3}{2})}{2^{2m}m!\Gamma(m+\nu+\frac{3}{2})}\quad (m\ge 0)\end{eqnarray*}$a_0=\displaystyle\frac{\sqrt{\pi}}{2^{\nu+1}\Gamma(\nu+\frac{3}{2})}$ ととると$$a_{2m}= \frac{(-1)^m\sqrt{\pi}}{2^{2m+\nu+1}m!\Gamma(m+\nu+\frac{3}{2})}$$よって微分方程式の特殊解 $y_1(x)$ は\begin{eqnarray*}y_1(x)&=& \sum_{m=0}^\infty \frac{(-1)^m\sqrt{\pi}}{2^{2m+\nu+1}m!\Gamma(m+\nu+\frac{3}{2})} x^{2m+\nu}\\ &=& \sqrt{\frac{\pi}{2x}} J_{\nu+\frac{1}{2}}(x) \\ &\equiv& j_\nu(x)\end{eqnarray*}

詳細は省きますがこれと独立な第2種球ベッセル関数 $n_\nu(x)$ を用いることで球ベッセル微分方程式の解は$$y(x)=c_1 j_\nu(x)+c_2 n_\nu(x)$$

ヘルムホルツ方程式の解まとめ

長くなりましたが以上から

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。