微分幾何学の講座・第13回。特定の形をもった曲面・立体の面積や体積のお話です。管状近傍の表面積に関するホテリングの定理や、曲面の近傍の体積に関するワイルの定理を紹介。重要なのは結果のみならず、動標構を活用したり変数変換をするといった、その過程にもあります。

フレネフレームは曲線に沿った立体を考えるのに便利なんだ!

ヤコビアンの計算もがんばろうね。
シリーズを通して読むとベターです。
前回はこちら:
 ダルブーフレームと測地的曲率・捩率・法曲率
ダルブーフレームと測地的曲率・捩率・法曲率
過去記事で学んだように、パラメータ表示された曲線に沿って変化する「動く座標系」のようなものを動標構といい、特にフレネフレームを導入しました。
弧長パラメータ表示された曲線 $\bm{C}(s)$ におけるフレネフレームは以下で定める単位接ベクトル $\bm{e}_1(s)$、単位主法線ベクトル $\bm{e}_2(s)$、単位従法線ベクトル $\bm{e}_3(s)$ の組である。\begin{eqnarray}\bm{e}_1(s)&:=&\bm{C}'(s)\tag{1a} \\ \bm{e}_2(s) &:=& \frac{\bm{C}''(s)}{|\bm{C}''(s)|}\tag{1b} \\ \bm{e}_3(s)&:=&\bm{e}_1(s)\times \bm{e}_2(s)\tag{1c}\end{eqnarray}
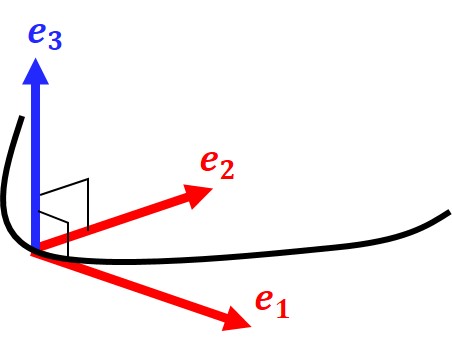
3つの単位ベクトルは正規直交基底をなすのでした。これをもとに曲率と捩率が定義されました。
\begin{equation}\kappa(s)=\bm{e}_1'(s)\cdot \bm{e}_2(s)\tag{2a}\end{equation}\begin{equation}\tau(s)=\bm{e}_2'(s)\cdot \bm{e}_3(s)\tag{2b}\end{equation}
さらにフレネフレームの変化は、それ自身の係数を曲率と捩率で表せて
\begin{equation}\frac{d}{ds}\begin{pmatrix}\bm{e}_1(s)\\\bm{e}_2(s)\\\bm{e}_3(s)\end{pmatrix}=\begin{pmatrix}0 & \kappa(s) & 0\\-\kappa(s) & 0 & \tau(s)\\0 & -\tau(s) & 0\end{pmatrix}\begin{pmatrix}\bm{e}_1(s)\\\bm{e}_2(s)\\\bm{e}_3(s)\end{pmatrix}\tag{3}\end{equation}
となるのでした。
3次元空間内に、チューブ状の立体である管状近傍を次のように定義します。
弧長パラメータ表示された空間曲線 $C:=\bm{C}(s)\in\mathbb{R}^3$ の $s_1\le s\le s_2$ の部分に対し、管状近傍 $B_r(C)$ を次のように定義する。\begin{equation}B_r(C):=\left\{\bm{C}(s)+u\bm{e}_2(s)+v\bm{e}_3(s)\in\mathbb{R}^3| s_1\le s\le s_2\;,\;u^2+v^2\le r^2\right\}\tag{4}\end{equation}なお $r>0$ は十分に小さい。
$C$ からの距離が $r$ 以下の点で成る立体から両端の半球を取り除いたものといえるでしょう。$r$ が小さいと断っているのは、立体が自己交差してしまう可能性を除くためです。
定義を見て、管状近傍が曲線に沿ったチューブ状の立体であることは想像できます。$\bm{C}(s)$ は曲線上のある点で、$\bm{e}_2(s)$ , $\bm{e}_3(s)$ はそこでの法平面をなします。$u,v$ をその係数とすることで法平面上の円を表しています。
曲線の長さを $L$ 、その管状近傍の体積を $\mathrm{vol}(B_r(C))$ とすると
\begin{equation}\mathrm{vol}(B_r(C)) = \pi r^2\cdot L\tag{5}\end{equation}
曲線の形に関わらず、管状近傍の断面積と曲線の長さがその体積になるというもの。円柱において(5)が成り立つのは当然ですが、ぐにゃりとまげても体積は同じというイメージです。まあそうだろうという感じもしますが、きちんと体積を計算してみましょう。
管状近傍 $B_r(C)$ にある点 $(x,y,z):=\bm{p}$ は(4)より\begin{equation}\bm{r}(s,u,v)=\bm{C}(s)+u\bm{e}_2(s)+v\bm{e}_3(s)\tag{6}\end{equation}偏微分をゴリゴリ計算するとヤコビアンは\begin{eqnarray*}J &=&\begin{vmatrix}\dd{x}{s} & \dd{y}{s} & \dd{z}{s} \\ \dd{x}{u} & \dd{y}{u} & \dd{z}{u} \\\dd{x}{v} & \dd{y}{v} & \dd{z}{v}\end{vmatrix} \\&=& \dd{\bm{p}}{s}\cdot\left(\dd{\bm{p}}{u}\times\dd{\bm{p}}{v}\right) \\&=& \left(\bm{C}'(s)+u\bm{e}'_2(s)+v\bm{e}'_3(s)\right)\cdot\left(\bm{e}_2(s)\times\bm{e}_3(s)\right) \\&=& \left(\bm{e}_1(s)+u\bm{e}'_2(s)+v\bm{e}'_3(s)\right)\cdot\bm{e}_1(s)\quad(\because(1))\\&=&\left(\bm{e}_1(s)+u(-\kappa(s)\bm{e}_1(s)+\tau(s)\bm{e}_3(s))-v\tau(s)\bm{e}_2(s)\right)\cdot\bm{e}_1(s)\quad(\because(3))\\&=& 1-u\kappa(s)\end{eqnarray*}半径 $r$ が十分小さいので $u$ も小さいです。ゆえに$$J=1-u\kappa(s)>0$$したがって管状近傍の体積は $s_1=0$ , $s_2=L$ として\begin{eqnarray*} \mathrm{vol}(B_r(C)) &=& \iiint_{B_r(C)}dxdydz \\&=&\iiint (1-u\kappa(s)) dsdudv \\&=&\int_0^L ds\iint_{u^2+v^2\le r^2}dudv(1-u\kappa(s)) \\&=& \int_0^L ds\iint_{u^2+v^2\le r^2}dudv -\int_0^L \kappa(s)ds\iint_{u^2+v^2\le r^2}ududv\\&=& \pi r^2L-\int_0^L \kappa(s)ds\int_0^r \int_0^{2\pi}r^2\cos\t d\t dr \\&=& \pi r^2 L\end{eqnarray*}よって(5)が示されました。
チューブ型である管状近傍の境界 $\partial B_r(C)$ は曲面です。$0\le s\le L$ の管であるとして、この表面積を求めましょう。
曲面は(4)を少しいじることで次のようにパラメータ表示できます。\begin{equation}\partial B_r(C)=\left\{\bm{C}(s)+r\cos\t\bm{e}_2(s)+r\sin\t\bm{e}_3(s)\in\mathbb{R}^3\left| \begin{matrix}0\le s\le L,\\0\le\t\le 2\pi\end{matrix}\right.\right\}\tag{7}\end{equation}この上の点 $(x,y,z)=\bm{p}$ とおくと$$\bm{p}(s,\t)=\bm{C}(s)+r\cos\t\bm{e}_2(s)+r\sin\t\bm{e}_3(s)$$曲面の面積の計算方法はこちらで解説しました。つまり\begin{equation}\mathrm{vol}(\partial B_r(C)) = \int_0^Lds\int_0^{2\pi}d\t \left|\dd{\bm{p}}{s}\times\dd{\bm{p}}{\t}\right|\tag{8}\end{equation}(1)(2)(3)を使いながら偏微分を実行して外積をとります。$$\dd{\bm{p}}{s}\times\dd{\bm{p}}{\t}=r(r\kappa(s)\cos\t -1)(\cos\t\bm{e}_2(s)+\sin\t \bm{e}_3)$$$r$ が小さいことを仮定してこの絶対値をとると$$ \left|\dd{\bm{p}}{s}\times\dd{\bm{p}}{\t}\right|=r(1-r\kappa(s)\cos\t)$$あとは簡単な積分計算により、求める表面積は\begin{equation}\therefore\quad\mathrm{vol}(\partial B_r(C)) =2\pi r L\tag{9}\end{equation}こちらもやはり、ぐにゃりと曲がっていても円柱と同じ式が成り立つのです。
曲面の前提知識としてざっと書いておきます。以下を参考にしてください:
空間内の曲面:パラメータ表示、接平面、法ベクトル、ガウス写像、面積
領域 $D$ で定義されるパラメータ $u,v$ を用いて、空間内の曲面は\begin{equation}\bm{S}(u,v):=\bigl(x(u,v),y(u,v),z(u,v)\bigr)\;,\quad u,v\in D\tag{10}\end{equation}と表現される。
曲面上の点 $\bm{S}(u_0,v_0)$ において$$\dd{\bm{S}}{u}(u_0,v_0)\quad,\quad\dd{\bm{S}}{v}(u_0,v_0)$$の2つは曲面の接ベクトルである。
曲面上の点 $\bm{S}(u,v)$ における単位法ベクトルを次で定義する。\begin{equation}\bm{n}(u,v):=\frac{\bm{S}_u\times\bm{S}_v}{|\bm{S}_u\times\bm{S}_v|}\tag{11}\end{equation}
さらにこちらで学んだように、第1基本量は\begin{equation}E:=\bm{S}_u\cdot \bm{S}_u \;,\quad F:=\bm{S}_u\cdot \bm{S}_v\;,\quad G:=\bm{S}_v\cdot \bm{S}_v\tag{12}\end{equation}第2基本量は\begin{equation}L:=\bm{S}_{uu}\cdot \bm{n}\;,\quad M:=\bm{S}_{uv}\cdot \bm{n}\;,\quad N:=\bm{S}_{vv}\cdot \bm{n}\tag{13}\end{equation}と定義されます。なお第2基本量については\begin{equation}L=-\bm{S}_{u}\cdot \bm{n}_{u}\;,\quad M=-\bm{S}_{u}\cdot \bm{n}_{v}\;,\quad N=-\bm{S}_{v}\cdot \bm{n}_{v}\tag{14}\end{equation}とも書けます。
これらを用いて平均曲率およびガウス曲率は\begin{eqnarray}H &=& \frac{EN-2FM+GL}{2(EG-F^2)}\tag{15a} \\ K &=& \frac{LN-M^2}{EG-F^2}\tag{15b}\end{eqnarray}
$(u,v)\in D$ で定義される空間内の曲面 $S:=\bm{S}(u,v)$ のサイズ $r$ の近傍 $U_r(S)$ とは\begin{equation}U_r(S):=\left\{\bm{S}(u,v)+t\bm{n}(u,v)|(u,v)\in D\;,\; -r\le t\le r\right\}\tag{16}\end{equation}ただし $r>0$ は十分小さい。
曲面 $\bm{S}(u,v)$ に厚み $2r$ をもたせたものといえます。その際、曲面に対して垂直な方向を考えるため単位法ベクトル $\bm{n}$ が現れています。自己交差を避けるために $r$ を小さいものと仮定しています。
$U_r(S)$ は立体です。この体積を求めましょう。$$\mathrm{vol}(U_r(S))=\iiint_{U_r(S)}dxdydz$$変数変換のために偏微分とヤコビアンの計算が要ります。$(x,y,z):=\bm{p}(t,u,v)$ とおいて\begin{eqnarray*}J &=&\dd{\bm{p}}{t}\cdot\left(\dd{\bm{p}}{u}\times\dd{\bm{p}}{v}\right) \\&=& \bm{n}\cdot\left\{(\bm{S}_u+t\bm{n}_u)\times(\bm{S}_v+t\bm{n}_v)\right\}\end{eqnarray*}ワインガルテンの公式\begin{eqnarray}\bm{n}_u &=& \frac{FM-GL}{EG-F^2} \bm{S}_u +\frac{FL-EM}{EG-F^2} \bm{S}_v\tag{17a} \\ \bm{n}_v &=& \frac{FN-GM}{EG-F^2} \bm{S}_u +\frac{FM-EN}{EG-F^2} \bm{S}_v\tag{17b}\end{eqnarray}を用いて\begin{eqnarray*}J &=& \bm{n}\cdot\left[\left\{\left(1+\frac{FM-GL}{EG-F^2}t\right)\bm{S}_u+\frac{FL-EM}{EG-F^2}t\bm{S}_v\right\}\times\left\{\left(1+\frac{FM-EN}{EG-F^2}t\right)\bm{S}_v+\frac{FN-GM}{EG-F^2}t\bm{S}_u\right\}\right] \\&=& \left[\left(1+\frac{FM-GL}{EG-F^2}t\right)\left(1+\frac{FM-EN}{EG-F^2}t\right)-\frac{(FL-EM)(FN-GM)}{(EG-F^2)^2}t^2\right](\bm{S}_u\times\bm{S}_v)\cdot\bm{n}\end{eqnarray*}(11)より$$(\bm{S}_u\times\bm{S}_v)\cdot\bm{n}=|\bm{S}_u\times\bm{S}_v|$$であることを使うと$$J=\left(1+\frac{2FM-GL-EN}{EG-F^2}t+\frac{LN-M^2}{EG-F^2}t^2\right)|\bm{S}_u\times\bm{S}_v|$$(15)より\begin{equation}J=(1-2Ht+Kt^2)|\bm{S}_u\times\bm{S}_v|\tag{18}\end{equation}ただし $H,K,\bm{S}_u,\bm{S}_v$ は $u,v$ の関数であることを忘れないでおきましょう。このヤコビアンによって積分計算すると\begin{eqnarray*}\mathrm{vol}(U_r(S)) &=& \iint_D\left\{\int_{-r}^r(1-2H(u,v)t+K(u,v)t^2)dt\right\}|\bm{S}_u(u,v)\times\bm{S}_v(u,v)|dudv \\&=& \iint_D\left(2r+\frac{2}{3}K(u,v)r^3\right)|\bm{S}_u(u,v)\times\bm{S}_v(u,v)|dudv \\&=& 2r\cdot\mathrm{vol}(S)+\frac{2}{3}r^3\iint_D K(u,v)|\bm{S}_u(u,v)\times\bm{S}_v(u,v)|dudv\end{eqnarray*} ここで $\mathrm{vol}(S)$ は曲面 $S$ の面積です。第1項はそれに厚み $2r$ をかけたものです。ガウス曲率がゼロなら第2項は消えます。この第2項は曲面の面積要素$$d\omega := |\bm{S}_u\times\bm{S}_v|dudv$$と書くことにすると
\begin{equation}\mathrm{vol}(U_r(S))=2r\cdot\mathrm{vol}(S)+\iint_D K d\omega\tag{19}\end{equation}
ガウス曲率の積分はガウス・ボネの定理にも現れます。その意味するところについては、いつか書くかもしれません。
$(u,v)\in D$ で定義される空間内の曲面 $S:=\bm{S}(u,v)$ を、厚みをもたせる方向に微小量 $\epsilon>0$ だけずらしてできる曲面 $\bm{S}_\epsilon:=\bm{S}+\epsilon\bm{n}$ を考えます(曲面の変分)。これの面積を求めてみましょう。つまり$$\mathrm{vol}(\bm{S}_\epsilon)=\iint_D\left|\dd{\bm{S}_\epsilon}{u}\times\dd{\bm{S}_\epsilon}{v}\right|dudv$$外積の部分は(18)とほとんど同様の計算で進めます。すると$$\mathrm{vol}(\bm{S}_\epsilon)=\iint_D(1-2\epsilon H(u,v)+\epsilon^2K(u,v))\left|\bm{S}_u\times\bm{S}_v\right|dudv$$\begin{equation}\therefore\quad \mathrm{vol}(\bm{S}_\epsilon)=\mathrm{vol}(S)-2\epsilon\iint_D H d\omega+O(\epsilon^2)\tag{20}\end{equation}(20)によれば、変分をとったとき、曲面の面積の変化率は平均曲率の積分であるということになります。変分をとる際、パラメータの範囲 $D$ が固定されていることに注意しましょう。$S$ の面積が極小であれば $\iint_D H d\omega=0$ です。
より一般には、曲面の変分は $D$ 上の任意関数 $\eta(u,v)$ に対して $\bm{S}+\epsilon\eta\bm{n}$ ととります。この場合も同様に計算すると $\iint_D H\eta d\omega=0$ となります。$\eta$ はまったく任意であるため、平均曲率 $H$ が至るところゼロという結論になります(このあたりの議論は「変分法」を勉強してみてください)。$H(u,v)=0$ をみたす曲面を極小曲面と言います。
・中内伸光『幾何学は微分しないと』
『幾何学は微分しないと』を参照しました。オヤジギャグまじりの平易な文章で微分幾何学を分かりやすく解説しています。初学者向けな分、内容はやや薄いと思うので、ネットや他の書籍を併用すると学習効果が高まります。

新装版 幾何学は微分しないと 〜微分幾何学入門〜【Amazon】
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

