Ramanujan's Master Theorem\begin{equation}\int_0^\infty x^{s-1}\sum_{n=0}^\infty \phi(n)(-x)^n dx=\frac{\pi}{\sin\pi s}{\phi(-s)}\tag{1}\end{equation}あるいは\begin{equation}\int_0^\infty x^{s-1}\sum_{n=0}^\infty \frac{\lambda(n)}{n!}(-x)^n dx=\G(s)\lambda(-s)\tag{1'}\end{equation}を複素解析により導出し、その応用例を挙げる。
ラマヌジャンによるメリン変換に関する公式です。さまざまな積分計算に応用できます。
参考にしたのはG. H. Hardy, "Ramanujan: Twelve Lectures on subjects suggested by his life and work" (1940)の§11.4です。以下、単にHardyとよびます。本記事では留数計算によって定理を導出するのですが、この文献の証明を追うのに、行間の埋めが不十分になってしまっている点があることを断っておきます。どうしても分からない部分があったのです。調べても調べても、詳細に解説している文献は見当たらず。。。補足していただける方、大歓迎です。
$z=u+iv$ とします。$\d>0$ に対し $\mathfrak{R}z\ge -\d$ の領域を $H(\d)$ と表すことにします。$\forall z\in H(\d)$ において関数 $\phi(z)$ は正則で\begin{equation}|\phi(z)|<C e^{Pu+A|v|}\quad\quad C,P,A:\mathrm{const.}\tag{2}\end{equation}を満たすとします。つまり $z$ が原点から遠ざかるときに $|\phi(z)|$ の増し方は指数的かそれ以下であるということです。このような条件を"growth condition"といい(どなたか邦訳教えてください)、今の場合は特に"exponential type"とよびます。(2)の場合に\begin{equation}\phi(z)\in\mathscr{R}(A,P,\d)\tag{3}\end{equation}と書くことにします。
定数 $A$ , $\d$ にも次の条件を附します。\begin{equation}A<\pi\;,\; 0<\d<1\tag{4}\end{equation}
$0<x<e^{-P}$ なる $x$ に対して、関数 $\Phi(x)$ を\begin{equation}\Phi(x):=\sum_{n=0}^\infty \phi(n)(-x)^n\tag{5}\end{equation}を定義します。交代級数で表される関数です。
さらに複素関数\begin{equation}f(z):=\frac{\pi}{\sin\pi z}\phi(-z)x^{-z}\tag{6}\end{equation}を定義します。$\phi(z)$ は $H(\d)$ で定義されますので、$f(z)$ は $u=\mathfrak{R}z\le \d$ で定義されます。Hardyは積分路を明示することなく、単にコーシーの定理により$$\Phi(x)=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\frac{\pi}{\sin\pi z}\phi(-z)x^{-z}dz$$が成立すると書いています。
詳細にこれを示せるでしょうか。この関数に対して下図の経路で周回積分をします。ただし $0<c<\d<1$ です。
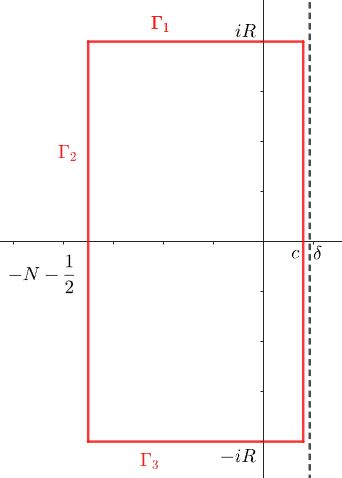
初等的な計算により $z=u+iv$ について\begin{equation}2|\sin\pi z|=2|\sin\pi z^*|=\sqrt{e^{2\pi v}+e^{-2\pi v}-2\cos2\pi u} \tag{7}\end{equation}$e^{2\pi v}+e^{-2\pi v}$ は $v=0$ のときに最小値 $2$ をとりますが、直線上では$0<u<1$ より $\cos2\pi u\neq 1$ , $\G_2$ でも実軸上の整数の点は避けているため $1/|\sin\pi z|$ は有界です。\begin{equation}\oint f(z)dz = \int_{c-i\infty}^{c+i\infty}f(z)dz+\left(\int_{\G_1}+\int_{\G_2}+\int_{\G_3}\right)f(z)dz\tag{8}\end{equation}$\G_1,\G_2,\G_3$ については $z\to -z$ と置換して\begin{eqnarray*}\int f(z)dz &=& \pi\int\frac{\phi(z)}{\sin\pi z}e^{z\ln x}dz \end{eqnarray*}ただし経路は置換後のもので、$H(\d)$ 内にあるコの字形です。それぞれ $\G_1',\G_2',\G_3'$ としましょう。ここでHardyでは現れなかった仮定\begin{equation}0<x\le e^{-P'}<e^{-P}\tag{9}\end{equation}を用いて、これらの経路においては\begin{eqnarray*}\left|\int f(z)dz\right|&\le& \pi\int\left|\frac{\phi(z)}{\sin\pi z}e^{z\ln x}\right||dz| \\ &=& \pi\int\frac{|\phi(z)|}{|\sin\pi z|}\left|e^{z\ln x}\right||dz|\\&<& \pi C\int\frac{e^{Pu+A|v|}}{|\sin\pi z|}e^{-P'u}|dz|\quad(\because(2)(4)(9))\\&=& \pi C\int\frac{e^{-(P'-P)u+A|v|}}{|\sin\pi z|}|dz|\end{eqnarray*}となります。この先で $\G_1$~$\G_3$ をどうしてもゼロに評価できず、仕方なく(9)を導入しました。ここで小さな数 $\epsilon:=P'-P>0$ とおき、上図の積分路について\begin{equation}\frac{1}{\epsilon^3}<\ln\frac{e^{2\pi R}+1}{2}<N<R^2-\frac{1}{2}-c\tag{10}\end{equation}となるように $N\in\NN$ , $R\in\RR$ を定めます。
すると\begin{eqnarray*}\left|\int_{\G_1'} f(z)dz\right|&\le&\pi C\int_{\G_1'}\frac{e^{-\epsilon u+A|v|}}{|\sin\pi z|}|dz|\\&=& \pi C\int_{-c}^{N+\frac{1}{2}}\frac{e^{-\epsilon u+AR}}{|\sin\pi(u-iR)|}du\quad(z=u-iR)\\&=& 2\pi C\int_{-c}^{N+\frac{1}{2}}\frac{e^{-\epsilon u+AR}}{\sqrt{e^{2\pi R}+e^{-2\pi R}-2\cos2\pi u}}du\quad(\because(7))\\&\le&2\pi C\int_{-c}^{N+\frac{1}{2}}\frac{e^{-\epsilon u+AR}}{e^{\pi R}-1}du\\&\le&2\pi C\frac{e^{\epsilon c+AR}(N+\frac{1}{2}+c)}{e^{\pi R}-1}\\&=&2\pi Ce^{\epsilon c}\frac{e^{-(\pi -A)R}(N+\frac{1}{2}+c)}{1-e^{-\pi R}}\\&<& 2\pi Ce^{\epsilon c}\frac{e^{-(\pi -A)R}R^2}{1-e^{-\pi R}}\quad(\because(10))\end{eqnarray*}\begin{equation}\therefore\quad\int_{\G_1'} f(z)dz\xrightarrow[]{\epsilon\to+0}0\tag{11}\end{equation}同様に\begin{equation}\int_{\G_3'} f(z)dz\xrightarrow[]{\epsilon\to+0}0\tag{12}\end{equation}また\begin{eqnarray*}\left|\int_{\G_2'} f(z)dz\right|&\le&\pi C\int_{\G_2'}\frac{e^{-\epsilon u+A|v|}}{|\sin\pi z|}|dz|\\&=&\pi C\int_{-R}^R\frac{e^{-\epsilon(N+1/2) +A|v|}}{|\sin\pi (N+\frac{1}{2}+iv)|}dv \\&=& 2\pi C\int_{-R}^R\frac{e^{-\epsilon(N+1/2) +A|v|}}{\sqrt{e^{2\pi v}+e^{-2\pi v}+2}}dv\\&=&2\pi Ce^{-\epsilon(N+1/2)}\int_{-R}^R\frac{e^{A|v|}}{e^{\pi v}+e^{-\pi v}}dv\\&=&4\pi Ce^{-\epsilon(N+1/2)}\int_0^R\frac{e^{2\pi v}e^{-(\pi-A)v}}{e^{2\pi v}+1}dv\\&<&4\pi Ce^{-\epsilon(N+1/2)}\int_0^R\frac{e^{2\pi v}}{e^{2\pi v}+1}dv\\&=& 2Ce^{-\epsilon(N+1/2)}\ln\frac{e^{2\pi R}+1}{2}\\&<& 2CNe^{-\epsilon N}\quad(\because(10))\\&<&2C\frac{N}{\frac{\epsilon^2 N^2}{2}}\\&=&\frac{4C}{\epsilon^2 N}\\&<&4C\epsilon\quad(\because(10))\end{eqnarray*}\begin{equation}\therefore\quad\int_{\G_2'} f(z)dz\xrightarrow[]{\epsilon\to+0}0\tag{13}\end{equation}
以上より(8)は$$\oint f(z)dz = \int_{c-i\infty}^{c+i\infty}f(z)dz$$$f(z)$ は $z=0,-1,-2\cdots$ に1位の極をもつので、留数定理を用いれば\begin{eqnarray*}\oint f(z)dz &=& 2\pi i \sum_{n=0}^\infty\lim_{z\to-n}\frac{\pi(z+n)}{\sin\pi z}\phi(-z)x^{-z}\\&=&2\pi i \sum_{n=0}^\infty\lim_{z\to n}\frac{\pi(z-n)}{\sin\pi (z-n)}\phi(z)(-x)^{z}\\&=& 2\pi i\sum_{n=0}^\infty \phi(n)(-x)^n\end{eqnarray*}したがって次の式を得ます。
\begin{equation}\Phi(x):=\sum_{n=0}^\infty \phi(n)(-x)^n=\frac{1}{2\pi i}\int_{c-i\infty}^{c+i\infty}\frac{\pi}{\sin\pi z}\phi(-z)x^{-z}dz\tag{14}\end{equation}
※ツイッターで積分経路の長方形の上辺(下辺)を半円に変えてはどうかと助言いただきました。後日検討するかもしれません。
この関数の定義域は $0<x<e^{-P}$ ですが、Hardyは
The series is usually divergent if $x>e^{-P}$ , but the integrand is majorised, for all positive $x$, by a multiple of $$e^{-(\pi -A)|v|}e^{-Pc}x^{-c}$$and the integral converges uniformly in any interval $0<x_0\le x\le X$ ; and therefore $\Phi(x)$ is regular, and represented by the integral, for all positive $x$.
G. H. Hardy, "Ramanujan: Twelve Lectures on subjects suggested by his life and work"
と述べ、定義域を $x>0$ へ拡張できるとしています。どういうことなのかさっぱり分かりませんが、これを認めて先へ進みましょう。
目標の(1)式を得るには(14)にMellin逆変換を施せばいいのですが、その変換を知らないものとして考えてみましょう。\begin{equation}s=\sigma+it\;,\;0<\sigma<\d<1\;,\;0<c_1<\sigma<c_2<\d\tag{16}\end{equation}と設定すると $c=c_1,c_2$ それぞれで(14)が成立します。すると $c=c_1$ において(14)より\begin{eqnarray*}\int_0^1\Phi(x)x^{s-1}dx&=&\frac{1}{2\pi i}\int_0^1x^{s-1}\left(\int_{c_1-i\infty}^{c_1+i\infty}\frac{\pi}{\sin\pi z}\phi(-z)x^{-z}dz\right)dx\\&=&\frac{1}{2\pi i}\int_{c_1-i\infty}^{c_1+i\infty}\frac{\pi}{\sin\pi z}\phi(-z)\left(\int_0^1x^{s-z-1}dx\right)dz\\&=&\frac{1}{2\pi i}\int_{c_1-i\infty}^{c_1+i\infty}\frac{\pi}{\sin\pi z}\frac{\phi(-z)}{s-z}dz\quad(\because\mathfrak{R}(s-z)=\sigma-c_1>0)\end{eqnarray*}$c=c_2$ においては\begin{eqnarray*}\int_1^\infty\Phi(x)x^{s-1}dx&=&\frac{1}{2\pi i}\int_1^\infty x^{s-1}\left(\int_{c_2-i\infty}^{c_2+i\infty}\frac{\pi}{\sin\pi z}\phi(-z)x^{-z}dz\right)dx\\&=&\frac{1}{2\pi i}\int_{c_2-i\infty}^{c_2+i\infty}\frac{\pi}{\sin\pi z}\phi(-z)\left(\int_1^\infty x^{s-z-1}dx\right)dz\\&=&\frac{-1}{2\pi i}\int_{c_2-i\infty}^{c_2+i\infty}\frac{\pi}{\sin\pi z}\frac{\phi(-z)}{s-z}dz\quad(\because\mathfrak{R}(s-z)=\sigma-c_2<0)\end{eqnarray*}これらを合わせると\begin{equation}\int_0^\infty\Phi(x)x^{s-1}dx =\frac{1}{2\pi i}\left(\int_{c_1-i\infty}^{c_1+i\infty}-\int_{c_2-i\infty}^{c_2+i\infty}\right)\frac{\pi}{\sin\pi z}\frac{\phi(-z)}{s-z}dz\tag{17}\end{equation}(17)の右辺に関して、2つの積分経路を含む長方形を考えると、上辺と下辺の積分はゼロで、被積分関数は長方形内部にある点 $z=s$ で1位の極をもちます。留数定理により$$\left(\int_{c_1-i\infty}^{c_1+i\infty}-\int_{c_2-i\infty}^{c_2+i\infty}\right)\frac{\pi}{\sin\pi z}\frac{\phi(-z)}{s-z}dz=-2\pi i\mathrm{Res}_{z=s}\frac{\pi}{\sin\pi z}\frac{\phi(-z)}{s-z}$$ゆえに$$\int_0^\infty \Phi(x)x^{s-1} dx=\frac{\pi}{\sin\pi s}{\phi(-s)}$$(5)より
\begin{equation}\int_0^\infty x^{s-1}\sum_{n=0}^\infty \phi(n)(-x)^ndx=\frac{\pi}{\sin\pi s}\phi(-s)\tag{18}\end{equation}
(18)で $\phi(z)=\frac{\lambda(z)}{\G(1+z)}$ おくと$$\int_0^\infty x^{s-1}\sum_{n=0}^\infty \frac{\lambda(n)}{n!}(-x)^n dx=\frac{\pi}{\sin\pi s}\frac{\lambda(-s)}{\G(1-s)}$$ガンマ関数の相反公式により
\begin{equation}\int_0^\infty x^{s-1}\sum_{n=0}^\infty \frac{\lambda(n)}{n!}(-x)^n dx=\G(s)\lambda(-s)\tag{19}\end{equation}
こちらをMaster Theoremとよぶこともあります。
(18)で $\phi(s)=1$ はgrowth conditionを満たし、\begin{equation}\int_0^\infty\frac{x^{s-1}}{1+x}dx=\frac{\pi}{\sin\pi s}\quad(0<s<1)\tag{20}\end{equation}を導きます。これは過去記事の"2023/2/3"で得た事実に一致します。
(18) で$\phi(s)=\frac{1}{\G(1+s)}$ あるいは(19)で $\lambda(s)=1$ とすればgrowth conditionを満たし\begin{equation}\int_0^\infty x^{s-1}e^{-x} dx=\G(s)\tag{21}\end{equation}を得ます。お馴染みの式ではありませんか!?もう少し一般化した $\lambda(s)=a^s$ なら\begin{equation}\int_0^\infty x^{s-1}e^{-ax} dx=\frac{\G(s)}{a^s}\tag{22}\end{equation}
(19)で $\lambda(s)=\frac{\G(a+s)}{\G(a)}$ とおくと\begin{equation}\int_0^\infty \frac{x^{s-1}}{(1+x)^a}dx=B(s,a-s)\tag{23}\end{equation}
一方(18)で $\phi(s)=\sin\pi s$ とすると左辺はゼロなので、定理は成立しません。$A<\pi$ でなく $A=\pi$ だからです。
(16)を見ると、(18)は $0<\mathfrak{R}s<\d$ で成り立っていました。$\phi(x+N)$ なる関数を(18)に適用すると$$\int_0^\infty x^{s-1}\sum_{n=0}^\infty \phi(n+N)(-x)^n dx=\frac{\pi}{\sin\pi s}{\phi(-s+N)}$$\begin{equation}\therefore\quad \int_0^\infty x^{s-1}\sum_{n=N}^\infty \phi(n)(-x)^ndx=\frac{\pi}{\sin\pi s}\phi(-s)\quad(-N<\mathfrak{R}s<-N+1)\tag{24}\end{equation}と表せます。$N=1$ , $\phi(s)=\frac{1}{\G(1+s)}$ では\begin{equation}\int_0^\infty x^{s-1}(e^{-x}-1)dx=\G(s)\quad(-1<\mathfrak{R}s<0)\tag{25}\end{equation}
(18)で $\phi(0)=\phi(1)=\phi(2)=\cdots=0$ とすると、関数 $\phi(z)$ は恒等的に $0$ となります。これをCarlsonの定理といいます(Hardy)。
G. H. Hardy, (1940) "Ramanujan: Twelve Lectures on Subjects Suggested by His Life and Work"
Wikipedia contributors. (2023). Carlson’s theorem. Wikipedia. [2023/5/24アクセス]
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。