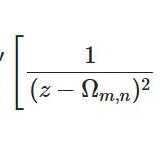前回は：
$$\O_{m,n}:=m\o_1+n\o_2$$とおくとワイエルシュトラスのペー関数は\begin{equation}\wp(z):=\frac{1}{z^2}+\sum_{m,n}'\left[\frac{1}{(z-\O_{m,n})^2}-\frac{1}{\O_{m,n}^{~2}}\right]\tag{1}\end{equation}と定義されます。ここで $\sum'$ は $m,n$ がともにゼロとなる場合を除き全整数にわたって和をとるものです。
前回はワイエルシュトラスのペー関数 $\wp(z)$ の級数展開をおこないました。今回はその展開式の係数（アイゼンシュタイン級数）を詳細に求めてみます。
$\wp(z)$ は $z=0$ で2位の極をもち、偶関数なのでした。展開式は\begin{equation}\wp(z)=\frac{1}{z^2}+a_2z^2+a_4z^4+a_6z^6+\cdots\tag{3}\end{equation}とひとまずおけて、定義式(1)の微分を繰り返して係数を求めると\begin{equation}a_{2k}=(2k+1)\sum_{m,n}'\frac{1}{\O_{m,n}^{~2k+2}}\tag{4}\end{equation}と分かります。ここで現れる級数\begin{equation}G_{2k}:=\sum_{m,n}'\frac{1}{\O_{m,n}^{~2k}}=\sum_{m,n}'\frac{1}{(m\o_1+n\o_2)^{2k}}\tag{5}\end{equation}をアイゼンシュタイン級数というのでした。(4)によればペー関数の展開式は、得体のしれないアイゼンシュタイン級数をひたすらに使用して表されることになります。
しかし後述するように、実はアイゼンシュタイン級数 $G_8,G_{10},G_{12},\cdots$ は $G_4,G_6$ ですべて表せてしまうのです。
前回で導いた等式\begin{equation}\wp'(z)^2-4\wp(z)^3+g_2\wp(z)+g_3=0\tag{6}\end{equation}に注目。（実はこれを微分すると楽なのですが）そのまま利用してみます。なお $g_2,g_3$ は\begin{equation}g_2:=60G_4\;,\quad g_3:=140G_6\tag{7}\end{equation}で定義され、(3)(4)(5)(7)より\begin{align}\wp(z)&=\frac{1}{z^2}+\frac{g_2}{20}z^2+\frac{g_3}{28}z^4+a_6z^6\\&\quad +a_8z^8+a_{10}z^{10}+a_{12}z^{12}+O(z^{14})\tag{8}\\\wp'(z)&=-\frac{2}{z^3}+\frac{g_2}{10}z+\frac{g_3}{7}z^3+6a_6z^5\\&\quad +8a_8z^7+10a_{10}z^9+12a_{12}z^{11}+O(z^{13})\tag{9}\end{align}(8)を3乗、(9)を2乗すると\begin{align}\wp(z)^3 &= \frac{1}{z^6}+\frac{3g_2}{20z^2}+\frac{3g_3}{28}+\left(\frac{3g_2}{400}+3a_6\right)z^2+\left(3a_8+\frac{3g_2g_3}{280}\right)z^4\\&+\left(\frac{g_2^3}{20^3}+3a_{10}+\frac{3g_2a_6}{10}+\frac{3g_3^2}{28^2}\right)z^6\\&+\left(3a_{12}+\frac{3g_2}{10}a^8+\frac{3g_3a_6}{14}+\frac{3g_2^2g_3}{20^2\cdot 28}\right)z^8+O(z^{10})\tag{10}\end{align}\begin{align}\wp'(z)^2 &=\frac{4}{z^6}-\frac{2g_2}{5z^2}-\frac{4}{7}g_3+\left(\frac{g_2^2}{100}-24a_6\right)z^2\\&+\left(\frac{g_2g_3}{35}-32a_8\right)z^4+\left(\frac{g_3^2}{49}+\frac{6a_6g_2}{5}-40a_{10}\right)z^6\\&+\left(\frac{12}{7}a_6g_3+\frac{8}{5}g_2a_8-48a_{12}\right)z^8+O(z^{10})\tag{11}\end{align}(8)(10)(11)を(6)に代入して係数を比較します。$z^2$ の係数から$$a_6=\frac{g_2^{~2}}{1200}$$であり、(4)より $a_6=7G_8$ でもあるので$$G_8=\frac{g_2^{~2}}{8400}=\frac{3}{7}G_4^{~2}$$ここで(7)を使いました。よってペー関数の6次の係数は $g_2$ あるいは $G_4$ で表すことができ、同時にアイゼンシュタイン級数についても $G_8$ を $G_4$ で表せることが分かりました。
同様に $z^4$ の係数を計算すると$$a_8=\frac{3g_2g_3}{6160}\quad,\quad G_{10}=\frac{15}{11}G_4G_6$$$z^6$ の係数を比較すると$$a_{10}=\frac{g_2^{~3}}{156000}+\frac{g_3^{~2}}{10192}\;,\quad G_{12}=\frac{18}{143}G_4^{~3}+\frac{25}{143}G_6^{~2}$$$z^8$ の係数を計算すると$$a_{12}=\frac{g_2^{~2}g_3}{184800}\quad,\quad G_{14}=\frac{30}{143}G_4^{~2}G_6$$
このように係数 $a_{2k}$ が次々と求まり、$g_2,g_3$ あるいは $G_4,G_6$ を使って表現できそうです。それは同時にアイゼンシュタイン級数 $G_{2k}$ も $G_4$ ,$G_6$ で表せるということでもあります。
\begin{align}\wp(z)&=\frac{1}{z^2}+\frac{g_2}{20}z^2+\frac{g_3}{28}z^4+\frac{g_2^{~2}}{1200}z^6\\&\quad +\frac{3g_2g_3}{6160}z^8+\left(\frac{g_2^{~3}}{156000}+\frac{g_3^{~2}}{10192}\right)z^{10}\\&\quad+\frac{g_2^{~2}g_3}{184800}z^{12}+O(z^{14})\end{align}
定理１は面倒な計算を経て導けました。この先も計算するには $a_{2k}$ の漸化式が分かればいいのですが。
そこで(6)を $z$ で微分します。\begin{equation}\wp''(z)=6\wp(z)^2-\frac{g_2}{2}\tag{12}\end{equation}これにペー関数の展開式\begin{align}\wp(z)&=\frac{1}{z^2}+\sum_{k=1}^\infty a_{2k}z^{2k}\\\wp''(z)&=\frac{6}{z^4}+\sum_{k=1}^\infty 2k(2k-1)a_{2k}z^{2k-2}\end{align}を代入します。$a_2=g_2/20$ であることにも留意して$$\sum_{k=2}^\infty k(2k-1)a_{2k}z^{2k-2}=6\sum_{k=2}^\infty a_{2k}z^{2k-2}+3\left(\sum_{k=1}^\infty a_{2k}z^{2k}\right)^2$$和の2乗になっているところはコーシー積をとります。\begin{align}\sum_{k=2}^\infty[k(2k-1)-6]a_{2k}z^{2k-2} &=3\left(\sum_{k=1}^\infty a_{2k}z^{2k}\right)^2\\&=3\sum_{k=2}^\infty\left(\sum_{l=1}^{k-1}a_{2l}a_{2k-2l}\right)z^{2k}\end{align}左辺の添え字をずらします。$$\sum_{k=1}^\infty[(k+1)(2k+1)-6]a_{2k+2}z^{2k}=3\sum_{k=2}^\infty\left(\sum_{l=1}^{k-1}a_{2l}a_{2k-2l}\right)z^{2k}$$左辺の和は $k=1$ で値ゼロなので$$\sum_{k=2}^\infty[(k+1)(2k+1)-6]a_{2k+2}z^{2k}=3\sum_{k=2}^\infty\left(\sum_{l=1}^{k-1}a_{2l}a_{2k-2l}\right)z^{2k}$$最後に係数を比較して
ペー関数の級数展開における係数について $k\ge2$ で次の漸化式が成り立つ。$$[(k+1)(2k+1)-6]a_{2k+2}=3\sum_{l=1}^{k-1}a_{2l}a_{2k-2l}$$
試しに計算してみると $3a_6=a_2^{~2}$ , $11a_8=3a_2a_4$ などとなります。定理２を使って係数をどんどん求めることができます。繰り返しになりますが $a_{2k}=(2k+1)G_{2k+2}$ なので、定理２を導いたことはすなわちアイゼンシュタイン級数の漸化式を得たことになります。
複素数 $g_2,g_3$ が与えられたとき、次の積分を考えます。\begin{equation}z=\int_\zeta^\infty(4t^3-g_2t-g_3)^{-\frac{1}{2}}dt\tag{13}\end{equation}(13)は根号の中身が3次多項式ですので楕円積分です。$\zeta$ は複素数で、積分経路は被積分関数の特異点すなわち $4t^3-g_2t-g_3$ の零点を通らないようにとられているとします。(13)を微分すると$$\frac{dz}{d\zeta}=-(4\zeta^3-g_2\zeta-g_3)^{-\frac{1}{2}}$$逆数をとって2乗すると\begin{equation}\left(\frac{d\zeta}{dz}\right)^2=4\zeta^3-g_2\zeta-g_3\tag{14}\end{equation}こちらの記事によって、(14)の解は定数 $\a$ を用いて$$\zeta=\wp(z+\a)$$と書けます（ただし、このペー関数の二重周期 $\o_1,\o_2$ は $g_2,g_3$ により適切に定められねばなりません。高度な内容なので今は気にしない）。十分遠方の $t$ で、積分(13)の被積分関数は $t^{-3/2}$ のオーダーとなりますので、この積分は収束します。よって $\zeta\to\infty$ のとき $z\to0$ です。ということは $z=-\a$ で $\zeta$ が発散しますので $\a$ は極です。すなわち $\a=\O_{m,n}$ で$$\zeta=\wp(z+\O_{m,n})$$ペー関数の周期性より\begin{equation}\zeta=\wp(z)\tag{15}\end{equation}(13)に適用すれば\begin{equation}z=\int_{\wp(z)}^\infty(4t^3-g_2t-g_3)^{-\frac{1}{2}}dt\tag{16}\end{equation}
以前、ヤコビの楕円関数を楕円積分の逆関数として定義しました。それに似て(16)はワイエルシュトラスのペー関数を楕円積分の逆関数として表示したものになっています。
ペー関数の定義は(1)で与えられました。この定義式では $\wp(z)$ がどんな関数なのかがとても分かりにくいと感じます。ところが(6)(16)などの関係式が得られると少しイメージしやすく、応用もききそうではないでしょうか。
次はこちら：
第５版です。いわずと知れた名著。楕円関数にかなりのページを割いています。
複素解析の超定番本です。
複素解析(Amazon)
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
