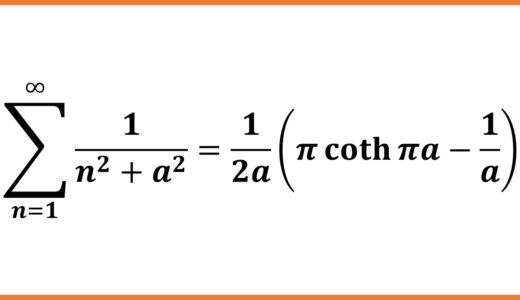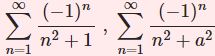\begin{equation}\sum_{n=1}^\infty\frac{1}{n^2+1}\tag{1}\end{equation}
これの値について考えます(第2弾)。
第1弾はこちら。フーリエ級数を用いたものです。
$\sin z$ は
\begin{equation}\sin z=z\prod_{n=1}^{\infty}\left(1-\frac{z^2}{n^2\pi^2}\right)\tag{2}\end{equation}
と表せます(無限乗積表示)。$\sin z=0$ の解が $z=0,\pm\pi,\pm 2\pi,\cdots$ であることから形式的にはうなずけると思います。
これについては以下も参考にしてください:
(2)の両辺の対数をとれば$$\log\sin z=\log z+\sum_{n=1}^{\infty}\log\left(1-\frac{z^2}{n^2\pi^2}\right)$$両辺を微分します。$$\cot z=\frac{1}{z}+\sum_{n=1}^{\infty}\frac{-2\frac{z}{n^2\pi^2}}{1-\frac{z^2}{n^2\pi^2}}$$このように無限乗積は対数をとれば無限和になり、微分すると分数をベースとした式の無限和になります。
以上より
\begin{equation}\cot z=\frac{1}{z}+2z\sum_{n=1}^{\infty}\frac{1}{z^2-n^2\pi^2}\tag{3}\end{equation}
(3)に $z=\pi i$ を代入しましょう。\begin{eqnarray*}\cot \pi i&=&\frac{1}{\pi i}+2\pi i\sum_{n=1}^{\infty}\frac{1}{-\pi^2-n^2\pi^2}\\&=&-\frac{i}{\pi}-\frac{2}{\pi} i\sum_{n=1}^{\infty}\frac{1}{n^2+1}\end{eqnarray*}ここで\begin{eqnarray*}\cot \pi i&=&\frac{\cos\pi i}{\sin\pi i}\\&=&i\frac{e^{-\pi}+e^{\pi}}{e^{-\pi}-e^{\pi}}\\&=&-i\frac{e^{\pi}+e^{-\pi}}{e^{\pi}-e^{-\pi}}\\&=&-i\coth\pi\end{eqnarray*}よって$$-i\coth\pi=-\frac{i}{\pi}-\frac{2}{\pi} i\sum_{n=1}^{\infty}\frac{1}{n^2+1}$$$$\coth\pi=\frac{1}{\pi}+\frac{2}{\pi} \sum_{n=1}^{\infty}\frac{1}{n^2+1}$$$$\pi\coth\pi=1+2\sum_{n=1}^{\infty}\frac{1}{n^2+1}$$と変形されて結局
\begin{equation}\therefore\;\sum_{n=1}^{\infty}\frac{1}{n^2+1}=\frac{1}{2}(\pi\coth\pi -1)\tag{4}\end{equation}
関数(今回は $\cot z$)を部分分数展開したりフーリエ級数で表すなどして,特定の値を代入すると無限級数の値が得られる例です。
以下の記事も併せてご覧ください。
同じものを複素フーリエ級数で導出しました:
類似した級数を複素フーリエ級数で導出しました:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。