\begin{equation}I=\int_0^1\frac{\cos\log x}{1+x^2}dx\tag{1}\end{equation}
$t=-\log x$ と置換します。$$I=\int_0^\infty\frac{\cos t}{e^t+e^{-t}}dt=\mathfrak{R}\int_0^\infty\frac{e^{it}}{e^t+e^{-t}}dt$$
ここで\begin{eqnarray*}J&&\equiv\oint_C\frac{e^{iz}}{e^z+e^{-z}}dz\\&&=\int_{-\infty}^{\infty}\frac{e^{it}}{e^t+e^{-t}}dt+\int_\G\frac{e^{iz}}{e^z+e^{-z}}dz\end{eqnarray*}
ただし $C$ は下図の周回積分(反時計回り)で、$\G$ は半径 $N\pi$ の大きな円弧部分です。
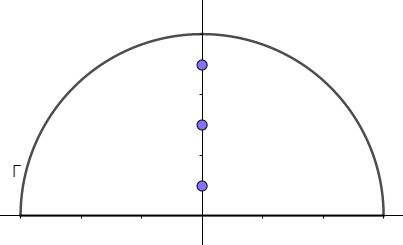
領域内の極は $\frac{\pi}{2},\frac{3\pi}{2},\frac{5\pi}{2}\cdots,N-\frac{\pi}{2}$ ですから、留数定理により\begin{eqnarray*}J&&=2\pi i\sum_{k=0}^{N-1}\mathrm{Res}_{z=(k+\frac{1}{2})\pi i}\frac{e^{iz}}{e^z+e^{-z}}\\&&=2\pi i\sum_{k=0}^{N-1}\displaystyle\lim_{z\to(k+\frac{1}{2})\pi i}\frac{e^{iz}}{e^z+e^{-z}}\left[z-\left(k+\frac{1}{2}\right)\pi i\right]\\&&=\pi i\sum_{k=0}^{N-1}\displaystyle\lim_{z\to(k+\frac{1}{2})\pi i}\frac{e^{(1+i)z}[2z-(2k+1)\pi i]}{e^{2z}-e^{(2k+1)\pi i}}\\&&=\pi i\sum_{k=0}^{N-1}e^{(1+i)(k+\frac{1}{2})\pi i}\frac{1}{e^{(2k+1)\pi i}}\\&&=\pi e^{-\frac{\pi}{2}}\frac{1-(-e^{-\pi})^N}{1+e^{-\pi}}\\&&\xrightarrow[N\to\infty]{}\frac{\pi}{2\cosh\frac{\pi}{2}}\end{eqnarray*}
\begin{equation}\therefore\quad\oint_C\frac{e^{iz}}{e^z+e^{-z}}dz=\frac{\pi}{2\cosh\frac{\pi}{2}}\tag{2}\end{equation}
これから$$\int_\G\frac{e^{iz}}{e^z+e^{-z}}dz\xrightarrow[N\to\infty]{}0$$を示します。
\begin{eqnarray*}\left|\int_\G\frac{e^{iz}}{e^z+e^{-z}}dz\right|&&\le N\pi\int_0^\pi\left|\frac{e^{-N\pi\sin\t}d\t}{e^{N\pi\cos\t}e^{iN\pi\sin\t}+e^{-N\pi\cos\t}e^{-iN\pi\sin\t}}\right|d\t\\&&\le N\pi\int_0^\pi\frac{e^{-N\pi\sin\t}d\t}{|e^{N\pi\cos\t}-e^{-N\pi\cos\t}|}d\t\end{eqnarray*}積分区間を半分に分けて、$[\frac{\pi}{2},\pi]$ のほうを $\t\to \pi-\t$ と置換すると\begin{eqnarray*}\left|\int_\G\frac{e^{iz}}{e^z+e^{-z}}dz\right|&&\le2N\pi\int_0^\frac{\pi}{2}\frac{e^{-N\pi\sin\t}d\t}{|e^{N\pi\cos\t}-e^{-N\pi\cos\t}|}d\t\\&&=2N\pi\int_0^\frac{\pi}{2}\frac{d\t}{|e^{\sqrt{2}N\pi\sin(\t+\frac{\pi}{4})}-e^{\sqrt{2}N\pi\sin(\t-\frac{\pi}{4})}|}d\t\end{eqnarray*}積分区間を半分に分けて、$[\frac{\pi}{4},\frac{\pi}{2}]$ のほうを $\t\to \frac{\pi}{2}-\t$ と置換すると\begin{eqnarray*}\left|\int_\G\frac{e^{iz}}{e^z+e^{-z}}dz\right|&&\le4N\pi\int_0^\frac{\pi}{4}\frac{d\t}{|e^{\sqrt{2}N\pi\sin(\t+\frac{\pi}{4})}-e^{\sqrt{2}N\pi\sin(\t-\frac{\pi}{4})}|}d\t\\&&=4N\pi\int_0^\frac{\pi}{4}\frac{e^{-N\pi\sin\t}d\t}{|e^{N\pi\cos\t}-e^{-N\pi\cos\t}|}d\t\\&&\le4N\pi\int_0^\frac{\pi}{4}\frac{e^{-N\pi\frac{2}{\pi}\t}d\t}{|e^{N\pi\cos\t}-e^{-N\pi\cos\t}|}d\t\\&&=2N\pi\int_0^\frac{\pi}{4}\frac{e^{-2N\t}d\t}{\sinh(N\pi\cos\t)}d\t\\&&\le\frac{2N\pi}{\sinh\frac{N\pi}{\sqrt{2}}}\int_0^\frac{\pi}{4}e^{-2N\t}d\t\\&&=\frac{2N\pi}{\sinh\frac{N\pi}{\sqrt{2}}}(1-e^{-\frac{\pi}{2}N})\\&&\xrightarrow[N\to\infty]{}0\end{eqnarray*}
(2)と冒頭とを合わせて$$\int_{-\infty}^{\infty}\frac{e^{it}}{e^t+e^{-t}}dt=\frac{\pi}{2\cosh\frac{\pi}{2}}$$実部を考えることにより$$\int_{-\infty}^{\infty}\frac{\cos t}{e^t+e^{-t}}dt=\frac{\pi}{2\cosh\frac{\pi}{2}}$$求める積分 $I$ はその半分ですので$$\int_0^1\frac{\cos\log x}{1+x^2}dx=\frac{\pi}{4\cosh\frac{\pi}{2}}$$
$$\int_0^1\frac{\cos\log x}{1+x^2}dx=\frac{\pi}{4\cosh\frac{\pi}{2}}$$
複素積分の記事:
 Excercise of Contour Integral (Combination of Real and Imaginary Axis)
Excercise of Contour Integral (Combination of Real and Imaginary Axis)
 【複素解析】フレネル積分-三角関数の特殊な積分 sin x^2 , cos x^2
【複素解析】フレネル積分-三角関数の特殊な積分 sin x^2 , cos x^2
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。


