$$I\equiv\int_0^\frac{\pi}{2}\frac{\arctan\sqrt{\tan x}}{\tan x}dx$$
積分bot からの出題です。とても苦労しました。
$y=\sqrt{\tan x}$ とおくと $dx=\frac{2ydy}{1+y^4}$ となりますので$$I=2\int_0^\infty\frac{\arctan y}{y(1+y^4)}dy$$よってこの積分は次のように書き換えられます。
\begin{equation}I=\int_{-\infty}^\infty\frac{\arctan x}{x(1+x^4)}dx\tag{1}\end{equation}
問題はここからです。区間を分けたり部分分数分解したり級数にしたり・・・と、実数の範囲でいろいろやろうとしたのですがダメでした。複素解析を使います。
この積分を複素平面で実践するときには、$\arctan z$ のbranch point(分岐点) である $z=\pm i$ に注意する必要があります。
次の周回積分(contour integral)を考えます。$$\oint_C\frac{\arctan z}{z(1+z^4)}dz$$
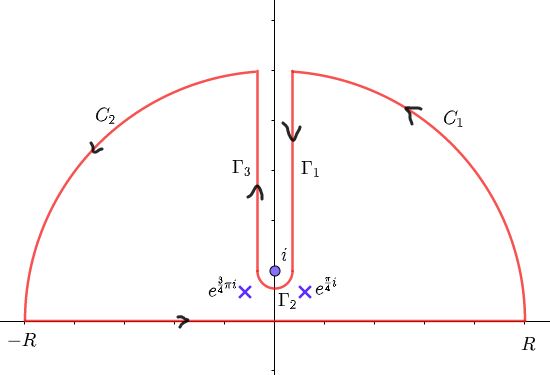
被積分関数は分母が$$z^4+1=(z-e^{\frac{\pi}{4}i})(z-e^{-\frac{\pi}{4}i})(z-e^{-\frac{3\pi}{4}i})(z-e^{\frac{3\pi}{4}i})$$と因数分解されることから、領域内で $z=e^{\frac{\pi}{4}i}$ , $e^{\frac{3}{4}\pi i}$ に1位の極(pole)を持ちます。また $\arctan z$ は $z=i$ に分岐点(branch point)をもつため、切断(cut)を虚軸の $[i,i\infty)$ に入れておきます。
留数定理
まずは周回積分の値を留数定理により求めます。極は先ほど挙げた2か所です。
\begin{eqnarray*}\oint_C\frac{\arctan z}{z(1+z^4)}dz&&=2\pi i\displaystyle\lim_{z\to e^{\frac{\pi}{4}i}}\frac{\arctan z}{z(1+z^4)}(z-e^{\frac{\pi}{4}i})+2\pi i\displaystyle\lim_{z\to e^{\frac{3\pi}{4}i}}\frac{\arctan z}{z(1+z^4)}(z-e^{\frac{3\pi}{4}i})\\&&=2\pi i\frac{\arctan e^{\frac{\pi}{4}i}}{e^{\frac{\pi}{4}i}(e^{\frac{\pi}{4}i}-e^{-\frac{\pi}{4}i})(e^{\frac{\pi}{4}i}-e^{\frac{3\pi}{4}i})(e^{\frac{\pi}{4}i}-e^{-\frac{3\pi}{4}i})}\\&&\quad+2\pi i\frac{\arctan e^{\frac{3\pi}{4}i}}{e^{\frac{3\pi}{4}i}(e^{\frac{3\pi}{4}i}-e^{-\frac{\pi}{4}i})(e^{3\frac{\pi}{4}i}-e^{\frac{\pi}{4}i})(e^{\frac{3\pi}{4}i}-e^{-\frac{3\pi}{4}i})}\\&&=-\frac{\pi i}{2}\left(\arctan e^{\frac{\pi}{4}i}+\arctan e^{\frac{3\pi}{4}i}\right)\end{eqnarray*}
$\tan$ の加法定理ですね。$\t_1=\arctan e^{\frac{\pi}{4}i}$ , $\t_2=\arctan e^{\frac{3\pi}{4}i}$ とおくと$$\tan\t_1=e^{\frac{\pi}{4}i}\;,\;\tan\t_2=e^{\frac{3\pi}{4}i}$$加法定理より$$\tan(\t_1+\t_2)=\frac{e^{\frac{\pi}{4}i}+e^{\frac{3\pi}{4}i}}{1-e^{\frac{\pi}{4}i}e^{\frac{3\pi}{4}i}}=\frac{i}{\sqrt{2}}$$$$\therefore\quad\t_1+\t_2=\arctan\frac{i}{\sqrt{2}}$$これを使うと
\begin{equation}\oint_C\frac{\arctan z}{z(1+z^4)}dz=-\frac{\pi i}{2}\arctan\frac{i}{\sqrt{2}}\tag{2}\end{equation}
複素関数arctan zの定義と計算
複素関数としての $\arctan z$ は次のように定義されます。
$$\arctan z\equiv\int_0^z\frac{du}{1+u^2}$$これを使って(2)の値を計算します。\begin{eqnarray*}\arctan\frac{i}{\sqrt{2}}&&=\int_0^\frac{i}{\sqrt{2}}\frac{du}{1+u^2}\\&&=\int_0^\frac{1}{\sqrt{2}}\frac{i dy}{1-y^2}\\&&=\frac{i}{2}\left[\log\frac{1+y}{1-y}\right]_0^\frac{1}{\sqrt{2}}\\&&=i\log(\sqrt{2}+1)\end{eqnarray*}
これで周回積分の値が求まりました。
\begin{equation}\oint_C\frac{\arctan z}{z(1+z^4)}dz=\frac{\pi}{2}\log(\sqrt{2}+1)\tag{3}\end{equation}
$C_1$ と $C_2$ の積分値がゼロに収束することを示します。
$\arctan z$ の定義における積分を実行することで$$\arctan z=-\frac{i}{2}\log\frac{1+iz}{1-iz}$$を得ます。原点から十分に遠い $C_1$ , $C_2$ 上では有界であることが分かります。よって$$|\arctan z|\le M$$なる定数 $M$ をとれます。
\begin{eqnarray*}\left|\int_{C_1}\frac{\arctan z}{z(1+z^4)}dz\right|&&\le M\left|\int_{C_1}\frac{1}{z(1+z^4)}dz\right|\\&&\le M\int_0^\frac{\pi}{2}\left|\frac{1}{(1+R^4e^{4i\t})}\right|d\t\\&&\le M\int_0^\frac{\pi}{2}\frac{1}{R^4-1}d\t\\&&\xrightarrow[R\to\infty]{}0\end{eqnarray*}$C_2$ についても同様にすればOKです。
\begin{equation}\int_{C_1}\frac{\arctan z}{z(1+z^4)}dz=\int_{C_2}\frac{\arctan z}{z(1+z^4)}dz=0\tag{4}\end{equation}
$\G_1$ と $\G_3$ は同じところの往復に見えます。ここで先ほどの公式$$\arctan z=-\frac{i}{2}\log\frac{1+iz}{1-iz}$$によって$$\int\frac{\arctan z}{z(1+z^4)}dz=-\frac{i}{2}\int\frac{\log(1+iz)-\log(1-iz)}{z(1+z^4)}dz$$偏角の範囲は$$-\frac{3}{2}\pi<\arg z<\frac{\pi}{2}$$とします。$$z=i+xe^{i\t}$$とおくと $\G_1$ では $z=i+xe^{\frac{\pi}{2}i}$、$\G_3$ では $z=i+xe^{-\frac{3\pi}{2}i}$ となります。したがって\begin{eqnarray*}\int_{\G_1}\frac{\arctan z}{z(1+z^4)}dz&&=-\frac{i}{2}\int_{\G_1}\frac{\log(1+iz)-\log(1-iz)}{z(1+z^4)}dz\\&&=-\frac{i}{2}\int_\infty^0\frac{\log(xe^{i\pi})-\log(2+x)}{i(1+x)(1+(1+x)^4)}idx\\&&=\frac{i}{2}\int^\infty_0\frac{\log x+i\pi-\log(2+x)}{(1+x)(1+(1+x)^4)}dx\end{eqnarray*}\begin{eqnarray*}\int_{\G_3}\frac{\arctan z}{z(1+z^4)}dz&&=-\frac{i}{2}\int_{\G_3}\frac{\log(1+iz)-\log(1-iz)}{z(1+z^4)}dz\\&&=-\frac{i}{2}\int_0^\infty\frac{\log(xe^{-i\pi})-\log(2+x)}{i(1+x)(1+(1+x)^4)}idx\\&&=-\frac{i}{2}\int^\infty_0\frac{\log x-i\pi-\log(2+x)}{(1+x)(1+(1+x)^4)}dx\end{eqnarray*}足し算すると\begin{eqnarray*}\left(\int_{\G_1}+\int_{\G_3}\right)\frac{\arctan z}{z(1+z^4)}dz&&=\frac{i}{2}\int^\infty_0\frac{2\pi i}{(1+x)(1+(1+x)^4)}dx\\&&=-\pi\int^\infty_1\frac{1}{y(1+y^4)}dy\quad(y=1+x)\\&&=-\pi\int^\infty_1\left(\frac{1}{y}-\frac{y^3}{1+y^4}\right)dy\\&&=-\frac{\pi}{4}\left[\log\frac{y^4}{1+y^4}\right]_1^\infty\\&&=-\frac{\pi}{4}\log2\end{eqnarray*}
\begin{equation}\left(\int_{\G_1}+\int_{\G_3}\right)\frac{\arctan z}{z(1+z^4)}dz=-\frac{\pi}{4}\log2\tag{5}\end{equation}
$\G_2$ は $\G_1$ と $\G_3$ につながっています。同様に $z=i+\epsilon e^{i\t}$ として $\frac{\pi}{2}$ から $-\frac{3}{2}\pi$ までの範囲となります。\begin{eqnarray*}\left|\int_{\G_2}\frac{\arctan z}{z(1+z^4)}dz\right|&&\le\frac{\epsilon}{2}\int_{-\frac{3}{2}\pi}^\frac{\pi}{2}\left|\frac{\log(i\epsilon e^{i\t})-\log(2-i\epsilon e^{i\t})}{(i+\epsilon e^{i\t})(1+(i+\epsilon e^{i\t})^4)}\right|d\t\\&&=\frac{\epsilon}{2}\int_{-\frac{3}{2}\pi}^\frac{\pi}{2}\left|\frac{\log\epsilon +i(\t+\frac{1}{2})-\log(2-i\epsilon e^{i\t})}{(i+\epsilon e^{i\t})(1+(i+\epsilon e^{i\t})^4)}\right|d\t\\&&\xrightarrow[\epsilon\to0]{}0\end{eqnarray*}
\begin{equation}\int_{\G_2}\frac{\arctan z}{z(1+z^4)}dz=0\tag{6}\end{equation}
$$\oint_C=\int_{-\infty}^\infty+\int_{C_1}+\int_{C_2}+\int_{\G_1}+\int_{\G_2}+\int_{\G_3}$$および(3)(4)(5)(6)より$$\frac{\pi}{2}\log(\sqrt{2}+1)=\int_{-\infty}^\infty\frac{\arctan x}{x(1+x^4)}dx-\frac{\pi}{4}\log2$$
$$\therefore\quad\int_{-\infty}^\infty\frac{\arctan x}{x(1+x^4)}dx=\frac{\pi}{2}\log(2+\sqrt{2})$$
したがって求める答えは
$$\int_0^\frac{\pi}{2}\frac{\arctan\sqrt{\tan x}}{\tan x}dx=\frac{\pi}{2}\log(2+\sqrt{2})$$
いろいろな積分記事:
 複素積分演習(cos(log x)/(1+x^2))
複素積分演習(cos(log x)/(1+x^2))
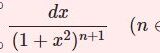 $\int\frac{dx}{(1+x^2)^{n+1}}$ 複素積分演習
$\int\frac{dx}{(1+x^2)^{n+1}}$ 複素積分演習
 Excercise of Contour Integral (Combination of Real and Imaginary Axis)
Excercise of Contour Integral (Combination of Real and Imaginary Axis)
 Integrals and Miscellaneous 1
Integrals and Miscellaneous 1
 Integrals and Miscellaneous 2
Integrals and Miscellaneous 2
 Integrals and Miscellaneous 3
Integrals and Miscellaneous 3
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

