以前の記事ではコサインの平方根 $\sqrt{\cos x}$ の定積分 について議論しました。
 $\int\sqrt{\cos x}dx$とガンマ関数・ベータ関数
$\int\sqrt{\cos x}dx$とガンマ関数・ベータ関数
ベータ関数の定義である$$B(x,y)=\int^1_0t^{x-1}(1-t)^{y-1}dt$$において $t=\sin^2\theta$ と置換すると、ベータ関数と三角関数の積分の関係$$B(x,y)=2\int_0^{\frac{\pi}{2}}\sin^{2x-1}\theta \cos^{2y-1}\theta d\theta$$を得ます。これを用いることで$$\int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx=\sqrt{\frac{2}{\pi}}\Gamma\left(\frac{3}{4}\right)^2$$という結果を導き出しました。ここでガンマ関数が出てくるのは$$B(x,y)=\frac{\Gamma(x)\Gamma(y)}{\Gamma(x+y)}$$なる関係式を使ったためです。
この方法を使えば $n$ 乗根でもできるのでは??と思ったので、考察してみました。
定積分 $I_n=\displaystyle\int_0^{\frac{\pi}{2}}\sqrt[n]{\cos x}dx$ はいかなる値か.
ベータ関数と三角関数の積分の関係式において $x=\dfrac{1}{2} , y=\dfrac{n+1}{2n}$ とおけば$$I_n= \frac{1}{2}B\left(\frac{1}{2},\frac{n+1}{2n}\right)$$ガンマ関数に書き直して$$I_n=\frac{1}{2}\cdot\frac{\Gamma(1/2)\Gamma(\frac{n+1}{2n})}{\Gamma(\frac{2n+1}{2n})}$$となりますが $\Gamma(1/2)=\sqrt{\pi}$ なので$$I_n=\frac{1}{2}\frac{\sqrt{\pi}\Gamma(\frac{n+1}{2n})}{\Gamma(\frac{2n+1}{2n})}$$を得ます。したがって$$\int_0^{\frac{\pi}{2}}\sqrt[n]{\cos x}dx=\frac{\sqrt{\pi}}{2}\frac{\Gamma(\frac{n+1}{2n})}{\Gamma(\frac{2n+1}{2n})}$$となりました!
\begin{equation}\int_0^{\frac{\pi}{2}}\sqrt[n]{\cos x}dx=\frac{\sqrt{\pi}}{2}\frac{\Gamma(\frac{n+1}{2n})}{\Gamma(\frac{2n+1}{2n})}\tag{1}\end{equation}
この積分を、Wolframでグラフの面積として確認してみます。
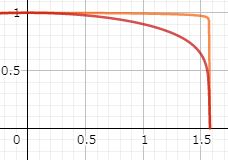
$n$が大きくなるにつれて、定積分の値を表すエリアが長方形になっていくのが分かります。これより$I_n$の極限は $\dfrac{\pi}{2}$ となりそうです。実際に(1)式の右辺の極限を考えると$$\lim_{n\to\infty}\int_0^{\frac{\pi}{2}}\sqrt[n]{\cos x}dx=\dfrac{\pi}{2}$$
~類題~
定積分 $I'_n=\displaystyle\int_0^{\frac{\pi}{2}}\sqrt[n]{\sin x}dx$ はいかなる値か.また,その $n\to\infty$ としたときの極限値はいくらか.
本記事とまったく同様の議論ですので、やってみてください😃
※ $\tan$ の $n$ 乗根でもやってみました!
 $\int\sqrt[n]{\tan x}dx$ とベータ関数
$\int\sqrt[n]{\tan x}dx$ とベータ関数
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
