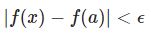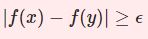関数の定義域内の任意の点を固定して連続性を示せば、その関数全体が連続であることが示せるのでした。今回はさらに条件の強い「一様連続性」について学びます。例題も少し示しますので、さらにいろいろな関数で挑戦してみて下さい。
前回は関数の連続性について、$\epsilon-\delta$ を用いて説明しました。
【ε論法】関数の連続性とδのテクニック
そのときは関数の定義域上の各点 $x=a$ を固定した上で $\epsilon$ に対し適切に $\delta$ を定めるということでしたので、 $\delta=\delta(a,\epsilon)$ という依存性がありました。これはちょうど関数列でいう「各点収束」に似ています。
今回はさらに条件の強い連続性「一様連続」について説明します。一様連続は $x$ を固定せずに $\delta$ を $\epsilon$ のみに依存する形で定め、$|f(x)-f(y)|<\epsilon$ と抑えられる連続性のことです。普通の連続性は各点がばらばらに収束する連続性を寄せ集めたようなものだったのに対し、今回は関数全体を同じような"スピード"で収束させるイメージです。なのでちょうど函数列でいう「一様収束」に似ています。
任意の$\epsilon>0$ に対してある$\delta>0$が存在し、$$|x-y|<\delta \Rightarrow |f(x)-f(y)|<\epsilon$$
普通の連続と何が違うのかというと
・普通の連続：先に $x=a$ が固定されていて $\delta$ は $a$ に依存してよい
・一様連続：先に $\delta$ が定められていて、$|x-y|<\delta$ なるあらゆる $x,y$ について$$|f(x)-f(y)|<\epsilon$$
ということです。
全実数で定義された $f(x)=x^2$ は連続ですが、一様連続ではありません。しかし定義域をせばめると一様連続になります。
$x\in[0,2]$ で定義される $f(x)=x^2$ は一様連続であることを示せ．
$$|f(x)-f(y)|=|x+y||x-y|<|x+y|\delta\le 4\delta$$最右辺は、関数が有界であるため $x,y$ はそれぞれ$2$以下というわけですね。よって任意の $\epsilon>0$ に対して $\delta=\epsilon/4$ ととれば$$|x-y|<\delta\Longrightarrow |f(x)-f(y)|<\epsilon$$となり、一様連続性が示されました。
【類題１】
(1) $x\in[0,2]$ で定義される $f(x)=x^3$ は一様連続であることを示せ．
(2) $x\in[-3,1]$ で定義される $f(x)=x^2-x$ は一様連続であることを示せ．
$x\in[1,4]$ で定義される $f(x)=1/x$ は一様連続であることを示せ．
$\delta=\epsilon$ と定めると$$|f(x)-f(y)|=\frac{|x-y|}{|xy|}<\frac{\delta}{|xy|}\le\delta=\epsilon$$となるので一様連続であると分かります。
【類題２】
(1) $x\in[1,2]$ で定義される $f(x)=\frac{1}{x^2}$ は一様連続であることを示せ．
(2) $x\in[1,2]$ で定義される $f(x)=\frac{1}{x+1}$ は一様連続であることを示せ．
全実数で定義された $f(x)=x^2$ は連続ですが一様連続ではありません。やってみると分かりますが $\delta$ はどうしても $x (y)$ に依存してしまいます。でも、だからといって一様連続を否定できるわけではありません。もっとうまく見つければ $\epsilon$ のみに依存する $\delta$ をとれるかもしれないからです。
では $f(x)=x^2$ が一様連続でないことの証明はどのようにするのでしょうか。次回の記事で書こうと思います。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
