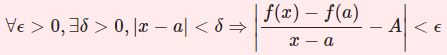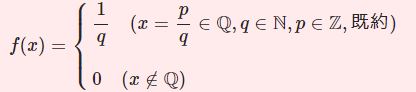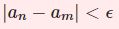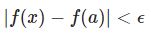ε-N論法を用いて数列がコーシー列でないことを証明する方法を、例題を通して解説する。コーシー列であることの証明は前回マスターしたがその否定はどうなるのだろうか？数列が収束しないことを証明する武器としてコーシー列の否定を学んでいこう。数列の収束、コーシー列の定義については過去記事を参照。
前回はコーシー列の定義を用いて、与えられた数列がコーシー列であることを証明する方法を学びました。実数の世界では、数列がコーシー列であることと収束することは同値なので、収束性を確かめるときにも便利であると説明しました。
【ε論法】数列がコーシー列であることの証明および収束性
ちなみに、そもそも $\epsilon-N$ 論法による収束の定義が何なのか知りたい場合は
【ε論法】数列の収束と極限・例題 ～εとNを使って～
をご覧ください。
今回は「コーシー列でない」ことを示す方法を解説します。これは数列が収束しないことと同値なので、収束しないことを証明したい場合にも使えます。
そもそも数列がコーシー列であるとは
任意の $\epsilon>0$ に対してある自然数 $N$ が存在し、$$m,n\ge N \Rightarrow |a_n-a_m|<\epsilon$$とできるとき、「コーシー列」という。
でした。要はこれの否定をとればいいわけですね。
ある $\epsilon>0$ が与えられたとき、任意の自然数 $N$ について $$|a_n-a_m|\ge\epsilon$$となるような $m,n\ge N$ が存在するとき、「コーシー列でない」という。
どうしてこのような文言になるのでしょうか。
コーシー列の定義ではまず「任意の $\epsilon>0$」という言葉があります。つまり $\epsilon=1,0.1,0.002,0.00004$ など、どんな数でも以下のホニャララが成り立ちますよ、という形です。その否定をとるなら、１つでもダメな $\epsilon$ があればいいわけですから、「ある $\epsilon>0$ においてホニャララが成り立たない」となります。
そのホニャララというのは、「ある $N$ が存在してムニャムニャ」ですからその否定は「任意の$N$についてムニャムニャでない」となります。ですからコーシー列の否定は「ある $\epsilon>0$ において、任意の $N$ についてムニャムニャでない」です。そのムニャムニャというのは、「任意の $m,n\ge N$ に対して$|a_n-a_m|<\epsilon$」ですので、その否定は「$|a_n-a_m|\ge\epsilon$ となる $m,n\ge N$ が存在する」です。これについては実際に $m,n$ の値を例示してやればいいです。
といっても何だか分かりにくいので、実践して感覚をつかんでいきましょう。
$a_n=(-1)^n$ はコーシー列でない。
$m,n\ge N$ に対し$$|a_n-a_m|=|(-1)^n-(-1)^m|$$ここで任意の自然数 $N$ に対して $m=2N+1 , n=2N$ とすると$$|a_n-a_m|=|(-1)^n-(-1)^m|=2$$です。ということは、$2$より小さい数$1$を $\epsilon$ とすることにより、以下が言えます。
$\epsilon=1$ とすると、任意の自然数$N$について$$m=2N+1 , n=2N \Rightarrow |a_n-a_m|=2\ge\epsilon$$差が $\epsilon$ より大きくなってしまうような $m,n$ が存在するというわけです。よってコーシー列でないといえます。
類題：$a_n=\cos\frac{n\pi}{4}$ はコーシー列でないことを示せ．
$$a_n=1+\displaystyle\frac{1}{2}+\cdots\frac{1}{n}$$はコーシー列でない。
$m\ge n$として一般性を失いません。$m,n\ge N$として$$|a_n-a_m|=\frac{1}{n+1}+\frac{1}{n+2}+\cdots+\frac{1}{m}$$右辺の項数は $m-n$ 個、また各項は $1/m$ 以上なので$$|a_n-a_m|\ge\frac{1}{m}+\frac{1}{m}+\cdots+\frac{1}{m}=1-\frac{n}{m}$$では $\epsilon=1/2$ とし、$m=3N$ , $n=N$ ととってみます。すると$$|a_n-a_m|\ge 1-\frac{N}{3N}=\frac{2}{3}>\epsilon$$となります。以上から、次のことが言えます。
$\epsilon=1/2$ とすると、任意の自然数 $N$ について$$m=3N , n=N \Rightarrow |a_n-a_m|\ge\epsilon$$となるためコーシー列ではない。
関連記事：
【ε論法】関数の連続性とδのテクニック
【ε論法】関数の一様連続性の証明
ε論法シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。