「悪魔の階段」とよばれる関数の連続性を示す．この関数の導入にあたっては予備知識として「カントール集合」が必要．カントール集合の定義と性質を紹介した後，悪魔の階段を関数列によって定義し，その関数列は連続かつ一様コーシーであることを証明するという流れである．
悪魔の階段は連続であることを示す．
もくじ
カントール集合の定義
カントール集合は，線分を3等分した真ん中の開区間を次々と除いてできる実数の集合です．除く操作は無限回行われますが，順に書いていけば $C_0=[0,1]$ , $C_1=[0,\frac{1}{3}]\cup[\frac{2}{3},1]$ , $C_2=[0,\frac{1}{9}]\cup[\frac{2}{9},\frac{1}{3}]\cup[\frac{2}{3},\frac{7}{9}]\cup[\frac{8}{9},1]$ ,$\cdots$ となります．カントール集合はこれらを用いて\begin{equation}C=C_\infty=\bigcap_{n=0}^\infty C_n\end{equation}と定義できます．
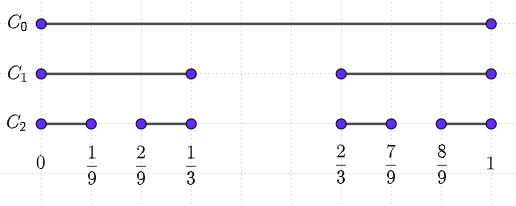
開区間を除いていって作られますので，$C_n$ は $2^n$ 個のdisjointな（ダブらない）閉区間で構成されていることになります．1つの閉区間の長さ（測度）は $\displaystyle\frac{1}{3^n}$ です．上図からも分かる通り，1度くり抜かれて $C_n$ から外れてしまった点は $C_{n+1}$ にも含まれません．なので補集合 $\overline{C_n}=[0,1]\setminus C_n$ に含まれる要素はそれより大きい $n$ でのすべての補集合にも含まれることになります．$n$ が大きくなるほど集合 $C_n$ はどんどん小さくなり，補集合 $\overline{C_n}$ は大きくなっていくのです。
(1) $\displaystyle\frac{1}{6}$ はカントール集合 $C$ に含まれないことを説明せよ．
(2) $C_n$ および $\overline{C_n}$ の長さを $n$ で表せ．
(1) $\frac{1}{9}<\frac{1}{6}<\frac{2}{9}$ より $\frac{1}{6}\notin C_2$．よって $C$ にも含まれない．
(2) 次節参照．
カントール集合の長さ
$C_n$ は長さ $\displaystyle\frac{1}{3^n}$ の閉区間 $2^n$ 個で成り立っているので全体の長さは\begin{equation}\mu(C_n)=\left(\frac{2}{3}\right)^n\end{equation}$n\to\infty$ の極限では $\mu(C)=0$ です．つまりカントール集合の長さ（測度）は $0$ となります．
例えば $C_n$ で閉区間の始点または終点になった点は、$n$ を大きくしてもずっと取り除かれないのでカントール集合に含まれます。このような点は $n$ を大きくしていくと無数に増えていくので、カントール集合には無数の点が含まれることになります．それでも長さが $0$ というのは「カントール集合は可算集合だから」と考えてもおかしくありません．ところが実は非可算集合なのです．
カントール集合は非可算
実際カントール集合は非可算であり，実数と同様に連続体濃度を持つことが分かっています．つまりカントール集合は連続体濃度をもち，かつ長さ（測度）$0$ というものなのです．
$[0,1]$ に含まれる実数を3進法で表すことにします．つまり $1/3=0.1$ , $2/3=0.2$ , $1/9=0.01$ , $7/9=0.21$ といった具合です．上で紹介した図の数値を3進法に直すと分かってくるのですが，カントール集合に含まれる実数は3進法で $0$ と $2$ しか現れないのです．例外として閉区間の端の $1/9=0.01$ , $7/9=0.21$ などはカントール集合に含まれていますが，最小桁の $1$ を $0222\cdots$ と書き直すことにより$$\frac{1}{9}=0.00222\cdots$$$$\frac{7}{9}=0.20222\cdots$$と表せます．以上を考慮すると「カントール集合 $C$ の任意の要素 $x$ は3進展開で $0$ と $2$ しか現れないものである」ということになります。なお $0,2$ で表せる各数の3進展開は1通りしかありません．
もしカントール集合が可算集合であればすべての要素を\begin{equation}C=\{x^1,x^2,\cdots,x^n,\cdots\}\end{equation}と書き表すことができます．これらの要素を3進法で表すと，$a_m^n=0\;\mathrm{or}\;2$ として$$\begin{cases}x^1&=&0.a^1_1a^1_2a^1_3\cdots\\x^2&=&0.a^2_1a^2_2a^2_3\cdots\\ x^3&=&0.a^3_1a^3_2a^3_3\cdots\\ &\vdots& \end{cases}$$ここで新たに $x\equiv0.a_1a_2a_3\cdots$ を以下のように定義します．$$\begin{cases}a_i=0\quad (\mathrm{if}\quad a_i^i=2)\\a_i=2\quad (\mathrm{if}\quad a_i^i=0)\end{cases}$$すると $x$ は $x^1,x^2\cdots$ のすべてと異なりますが $0,2$ のみで表せているので $x\in C$ となって矛盾です．よってカントール集合は非可算です．
(1) $\displaystyle\frac{1}{6}$ を3進法で表し，カントール集合に含まれないことを確認せよ．
(2) $\displaystyle\frac{1}{4}$ を3進法で表し，カントール集合に含まれることを確認せよ．
(1) 3進法で $\dfrac{1}{6}=0.01111\cdots$．1が現れているのでカントール集合に含まれない．
(2) 3進法で $\dfrac{1}{4}=0.02020\cdots$．1が現れていないのでカントール集合に含まれる．
カントール集合の定義を押さえたうえで，次に「カントール関数」別名「悪魔の階段」と呼ばれる関数を見ていきましょう．もう一度カントール集合の作り方を図示しておきます．以下，考える区間を $[0,1]$ に限定します．
悪魔の階段の定義
$x\in[0,1]$ において関数列 $g_n(x)$ を以下のように定義します．\begin{equation}g_n(x)\equiv\begin{cases}\left(\displaystyle\frac{3}{2}\right)^n&\quad& (x\in C_n)\\[1em]0&\quad& (x\notin C_n)\end{cases}\end{equation}先ほど述べたように $C_n$ は $2^n$ 個の閉区間からなりますから，$g_n(x)$ は $2^{n+1}-2$ 個の点で不連続です．よってほとんど至るところで連続であり，リーマン可積分です．
そこで次の積分からなる関数列 $f_n(x)$ を $x\in[0,1]$ 上で定義します．\begin{equation}f_n(x)\equiv\int^x_0g_n(t)dt\end{equation}微分積分学の基本定理から$$|f'_n(x)|=|g_n(x)|\le\left(\displaystyle\frac{3}{2}\right)^n$$つまり $f_n(x)$ は（リプシッツ）連続です．
区間の端っこを見てみましょう．明らかに $f_n(0)=0$ です．また前述したように $C_n$ の長さが $(2/3)^n$ ですから$$f_n(1)=\int^1_0g_n(t)dt=\int_{t\in C_n}\left(\frac{3}{2}\right)^ndt=1$$
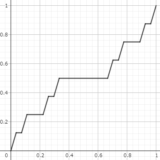
ここまでの議論から $f_n(x)$ の姿を確認してみましょう．$n=2$ においては\begin{equation}g_2(x)\equiv\begin{cases}\left(\displaystyle\frac{3}{2}\right)^2&\quad& (x\in C_2)\\[1em]0&\quad& (x\notin C_2)\end{cases}\end{equation}\begin{equation}f_2(x)=\int^x_0g_2(t)dt\end{equation}となっています．$g_2(x)=0$ の区間では $f_2(x)$ は水平で，ほかでは傾き $9/4$ の直線となっています．図で表すと下のようになります。階段っぽいですね．
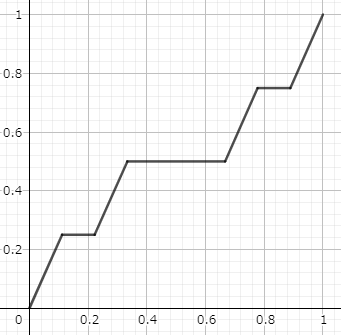
さらに $f_3(x)$ なら次のようになります．
いびつな階段って感じですね．この関数列 $f_n(x)$ を $n\to\infty$ とした極限 $f(x)$ を悪魔の階段（カントール関数）と言います．
$x\notin C_n$ における関数列 $f_n(x)$
$C_n$ は $2^n$ 個のdisjointな閉区間から成りますが，そのうちの任意の閉区間１つを $I$ と名付けます．すると $I$ の長さは $3^{-n}$ です．また $I\subset C_n$ ですから当然 $I$ 上では $g_n(x)=(3/2)^n$ です．よって\begin{equation}\int_{x\in I}g_n(x)dx=\left(\frac{3}{2}\right)^n\cdot3^{-n}=\frac{1}{2^n}\end{equation}さらに $I$ において，$I$ を3等分してできる真ん中の区間で $g_{n+1}(x)=0$，その残りの区間で $g_{n+1}(x)=(3/2)^{n+1}$ であることから\begin{equation}\int_{x\in I}g_{n+1}(x)dx=\left(\frac{3}{2}\right)^{n+1}\cdot3^{-n}\cdot\frac{2}{3}=\frac{1}{2^n}\end{equation}と同じ値になります．
$C_n$ は $I$ と同様の区間が $2^n$ 個集まってできていますから\begin{equation}\int_{x\in C_n}g_n(x)dx=\int_{x\in C_n}g_{n+1}(x)dx=1\end{equation}$C_n$ の閉区間に含まれない部分 $x\notin C_n$ においては $g_n(x)=0$ かつ $g_{n+1}(x)=0$ ですので積分区間に含めたところで積分値は変化しません．よって$C_n$ のいずれかの閉区間の終点（右端の点）を $a$ とすれば\begin{equation}\int_0^ag_n(x)dx=\int_0^ag_{n+1}(x)dx\tag{1}\end{equation}任意の $x\notin C_n$ を考え，$x$ の直前の閉区間の終点を $a$ とします． $[0,a]$ で積分すると式(1)が成り立ち，かつ $(a,x]\subset \overline{C_n}$ での積分値は $0$ ですから結局\begin{equation}\int_0^xg_n(x)dx=\int_0^xg_{n+1}(x)dx\quad(x\notin C_n)\end{equation}\begin{equation}\label{1004cantor2}\therefore f_{n+1}(x)=f_n(x)\quad(x\notin C_n)\tag{2}\end{equation}
$x\in C_n$ における関数列 $f_n(x)$
$x\in C_n$ とします。$C_n$ を構成する $2^n$ 個の閉区間のうち， $x$ を含むものを $I=[a,b]$ とします．先ほどの議論から $|g_n(x)-g_{n+1}(x)|$ の区間 $[0,a)$ までの積分値は $0$ です．従って\begin{eqnarray*}|f_n(x)-f_{n+1}(x)|&=&\left|\int_0^x(g_n(t)-g_{n+1}(t))dt\right|\\&=& \left|\int_a^x(g_n(t)-g_{n+1}(t))dt\right|\\&\le& \int_a^x|g_n(t)-g_{n+1}(t)|dt\\&\le& \int_a^b|g_n(t)-g_{n+1}(t)|dt\\&\le& \left(\frac{3}{2}\right)^n\cdot 3^{-n}\\&=&2^{-n}\end{eqnarray*}\begin{equation}\therefore |f_n(x)-f_{n+1}(x)|\le 2^{-n}\quad(x\in C_n)\tag{3}\end{equation}
関数列 $f_n(x)$ の一様収束性
任意の $x\in[0,1]$ は $C_n$ に含まれているかいないかのどちらかですから，式(2)(3)より\begin{equation}\therefore |f_n(x)-f_{n+1}(x)|\le 2^{-n}\quad(x\in [0,1])\tag{4}\end{equation}が成立します．このことを用いて $\{f_n(x)\}$ が一様収束であることを証明します．
任意の $\epsilon>0$ に対し $2^{N-1}\epsilon>1$ なる自然数 $N$ が存在します．式(4)から任意の自然数 $k$ に対して$$|f_k(x)-f_{k+1}(x)|\le 2^{-k}$$が成立します．ここで $m>n\ge N$ なる自然数 $m,n$ に対し\begin{eqnarray*}|f_m(x)-f_n(x)|&=&\left|\sum^{m-1}_{k=n}(f_{k+1}(x)-f_k(x))\right|\\&\le& \sum^{m-1}_{k=n}\left|f_{k+1}(x)-f_k(x)\right|\\&\le& \sum^{m-1}_{k=n}2^{-k}\\&=& 2^{-n}\frac{1-(1/2)^{m-n}}{1-1/2}\\&=& 2^{-n+1}\left[1-\left(\frac{1}{2}\right)^{m-n}\right]\\&<&2^{-n+1}\le 2^{-N+1}\\&<& \epsilon\end{eqnarray*}
従って関数列 $\{f_n(x)\}$ は一様コーシー列となります．もし $x$ を先に定めてしまうと $\{f_n(x)\}$ は関数列ではなく数列とみなせるのでただのコーシー列となりますが，今の場合 $x$ は任意ですので「一様」と言われます．一様コーシーな関数列は一様収束しますので，$\{f_n(x)\}$ は一様収束します．
一様コーシーについては
【ε論法】一様コーシーな関数列と一様収束性
を参照ください．
カントール関数 $f(x)$ の連続性
以上より関数列 $\{f_n(x)\}$ は一様収束かつ連続関数列であることからその収束先であるカントール関数 $f(x)$ も連続となります。
一様収束する関数列について参考：
【ε論法】関数列が一様収束でないことの証明
ε論法シリーズ
【２】無限積と級数の関係と収束性
【１】無限積の定義と収束・発散
絶対収束する二重級数・和の順序、コーシー積
正項の二重級数と和の順序
二重数列と二重級数（収束性と足し合わせの順）
実数論の練習問題
無限級数の収束性3（アーベル・ディリクレ）
シュトルツ・チェザロの定理（数列の極限）
【ε論法】極限の計算：limをεδに
【ε論法】ε-δ論法によって微分する・例題７つ
【ε論法】カントール集合と悪魔の階段の連続性
【ε論法】トマエ関数は有理数の点では不連続
【ε論法】連続関数の和も積も合成も連続関数
【ε論法】一様コーシーな関数列と一様収束性
【ε論法】関数列が一様収束でないことの証明
【ε論法】関数列の各点収束と一様収束
【ε論法】一様連続でないことの証明
【ε論法】関数の一様連続性の証明
【ε論法】関数の連続性とδのテクニック
【ε論法】コーシー列でないことの証明
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。