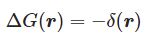物理においてポアソン方程式などを解く場合に現れるグリーン関数$G$を求める方法について説明する。デルタ関数、第1種ベッセル関数、フーリエ変換などの数学トピックが詰まっており勉強になると思う。この記事では、あせらず1次元からはじめて一般のN次元まで順にもっていく。
ポアソン方程式の解を求めたいときによく使われるグリーン関数の解法を見ていきます。
グリーン関数 $G$ は微分方程式\begin{equation}\Delta G(\boldsymbol{r})=-\delta(\boldsymbol{r})\end{equation}を満たす関数 $G$ です。$\delta(\boldsymbol{r})$ はディラックのデルタ関数です。例えばマクスウェル方程式の応用として点電荷がつくる静電ポテンシャルが満たす式\begin{equation}\Delta\phi(\boldsymbol{r})=-\frac{q}{\epsilon}\delta(\boldsymbol{r})\end{equation}にも現れます（この例は3次元）。なお上記の方程式ではデルタ関数は原点で無限大となっていますが、点 $\boldsymbol{r}'$ で無限大になる場合は\begin{equation}\Delta G(\boldsymbol{r},\boldsymbol{r}')=-\delta(\boldsymbol{r}-\boldsymbol{r}')\end{equation}と書き換えます。ただ文字が増えて邪魔くさいのでここでは原点に限定しておきます。
また、物理では上記のような3次元での解法が取り上げられることが多いですが、知識を拡大していきたいのでもっと一般的に $N$ 次元で考えていきます。よって今回のテーマは次のようになります。
$N$ 次元座標 $\boldsymbol{x}=(x_1,x_2,\cdots,x_N)$ に関するグリーン関数 $G(\boldsymbol{x})$ が満たす微分方程式\begin{equation}\Delta G(\boldsymbol{x})=-\delta^N(\boldsymbol{x})\end{equation}を解け．ここで $\delta^N(\boldsymbol{x})=\delta(x_1)\delta(x_2)\cdots\delta(x_N)$ であり，$N$ 次元のラプラシアン $\Delta$ は
$$\Delta \equiv\frac{\partial^2}{\partial x_1^2}+\frac{\partial^2}{\partial x_2^2}+\cdots \frac{\partial^2}{\partial x_N^2}$$で定義される微分作用素である．
あせらず1次元から順に見ていきたいと思います。
1次元の場合、グリーン関数 $G(x)$ が満たす微分方程式は $x$ 座標のみを用いて\begin{equation}\frac{d^2G}{dx^2}=-\delta(x)\end{equation}原点以外では $0$ なので1次関数となります。また連続性を仮定し $x<0$ において$G(x)=ax+b$ , $x>0$において $G(x)=cx+b$ とします。微分方程式の両辺を全空間で積分すると$$\left[\frac{dG}{dx}\right]^\infty_{-\infty}=-1 \Longrightarrow c-a=-1$$$$\therefore G(x)= \begin{cases} ax+b &(x<0) \\ (a-1)x+b &(x\geq0) \end{cases}$$となります。
原点について対称であると考えれば $a=1/2$ とすればよく、\begin{equation}G(x)=\frac{1}{2}|x|+b\end{equation}となります。これで1次元のグリーン関数が求まりました。$b$ の値も何か条件があれば決まったりします。色々な条件を仮定しましたが、物理で応用されることを考えてのことであり、純粋に方程式を解くだけならそこまで考えなくていいでしょう。
2次元の場合、座標を $\boldsymbol{x}=(x,y)$ と表し、グリーン関数 $G(\boldsymbol{x})$ が満たす微分方程式は
\begin{equation}\Delta G(\boldsymbol{x})=-\delta^2(\boldsymbol{x})\tag{1}\end{equation}ここで $\delta^2(\boldsymbol{x})=\delta(x)\delta(y)$ です。
$G$ をフーリエ変換すれば $\boldsymbol{k}=(k_x,k_y)$ として\begin{equation}\tilde{G}(\boldsymbol{k})=\int^\infty_{-\infty}G(\boldsymbol{x})e^{-i\boldsymbol{k}\cdot\boldsymbol{x}}d^2x\end{equation}ここで $d^2x=dxdy$ としています。さらに逆フーリエ変換すれば\begin{equation}G(\boldsymbol{x})=\frac{1}{4\pi^2}\int ^\infty_{-\infty} \tilde{G}(\boldsymbol{k})e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k\end{equation}となります。ここで $d^2k=dk_xdk_y$ を表し、以下このような記法をします。
これにラプラシアンを作用させて\begin{eqnarray}\Delta G(\boldsymbol{x}) &=& \frac{1}{4\pi^2}\int\tilde{G}(\boldsymbol{k})\Delta e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k\\ &=&\frac{1}{4\pi^2}\int\tilde{G}(\boldsymbol{k})\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}\right) e^{i(k_xx+k_yy)}d^2k\\&=&\frac{1}{4\pi^2}\int\tilde{G}(\boldsymbol{k})\{(ik_x)^2+(ik_y)^2\} e^{i(k_xx+k_yy)}d^2k\\&=&-\frac{1}{4\pi^2}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k\end{eqnarray}このラプラシアンは $x,y$ に関する微分作用素なので $\boldsymbol{k}$ にはかからないのがポイントです。ここで $k^2=k_x^2+k_y^2$ としています。
一方、デルタ関数 $\delta^2(\boldsymbol{x})=\delta(x)\delta(y)$ のフーリエ変換は\begin{equation}\delta^2(\boldsymbol{x})=\frac{1}{4\pi^2}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k\end{equation}
以上より(1)は以下のように書き換えられます。\begin{equation}-\frac{1}{4\pi^2}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k=-\frac{1}{4\pi^2}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k\end{equation}両辺を比べて
\begin{equation}\tilde{G}(\boldsymbol{k})=\frac{1}{k^2}\end{equation}となります。この逆変換が求める解であり、\begin{equation}G(\boldsymbol{x})=\frac{1}{4\pi^2}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^2k\end{equation}となります。これは全 $\boldsymbol{k}$ 平面にわたる積分です。$\boldsymbol{k}$ と $\boldsymbol{x}$ のなす角を $\theta$ とすると、$\boldsymbol{k}$ の極座標表示にこの $\theta$ を用いて差し支えありません。$$k_x=k\cos\theta\;,\;k_y=k\sin\theta$$$$d^2k=dk_xdk_y=kdkd\theta$$よって積分は\begin{equation}G(\boldsymbol{x})=\frac{1}{4\pi^2}\int^\infty_0dk\int^{2\pi}_0d\theta\frac{e^{ikr\cos\theta}}{k}\end{equation}ここで $|\boldsymbol{x}|=r$ としています。さらに変形して\begin{eqnarray}\int^{2\pi}_0\frac{e^{ikr\cos\theta}}{k}d\theta &=& \int^{\pi}_0\frac{e^{ikr\cos\theta}}{k}d\theta+\int^{2\pi}_\pi\frac{e^{ikr\cos\theta}}{k}d\theta\\&=&\int^{\pi}_0\frac{e^{ikr\cos\theta}}{k}d\theta+\int^0_\pi\frac{e^{ikr\cos(2\pi-\theta)}}{k}(-d\theta)\\&=&\int^{\pi}_0\frac{e^{ikr\cos\theta}}{k}d\theta+\int^\pi_0\frac{e^{ikr\cos\theta}}{k}d\theta\\&=&2\int^{\pi}_0\frac{e^{ikr\cos\theta}}{k}d\theta\end{eqnarray}ゆえに\begin{equation}G(\boldsymbol{x})=\frac{1}{2\pi^2}\int^\infty_0dk\int^{\pi}_0d\theta\frac{e^{ikr\cos\theta}}{k}\tag{2}\end{equation}
ところでHansen-Besselの公式によると第1種ベッセル関数 $J_n(z)$ は以下のように積分表示されます。\begin{equation}J_n(z)=\frac{1}{\pi i^n}\int^\pi_0e^{iz\cos\theta}\cos n\theta d\theta\tag{3}\end{equation}\begin{equation}\therefore\;\pi J_0(kr)=\int^\pi_0e^{ikr\cos\theta}d\theta\end{equation}この公式の導出に関しては別記事に詳述しています。
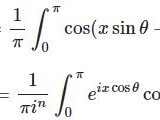第1種ベッセル関数の積分表示とその導出
これと(2)を比較すれば以下の表式を得ます。\begin{equation}G(\boldsymbol{x})=\frac{1}{2\pi}\int^\infty_0\frac{J_0(kr)}{k}dk\end{equation}
さて、$J_0$ の微分は\begin{equation}\frac{dJ_0(kr)}{dr}=\frac{1}{\pi}\int^\pi_0 ik\cos\theta e^{ikr\cos\theta} d\theta\end{equation}(3)から得られる等式\begin{equation}J_1(kr)=\frac{1}{\pi i}\int^\pi_0e^{ikr\cos\theta}\cos\theta d\theta\end{equation}を用いれば\begin{equation}\frac{dJ_0(kr)}{dr}=-kJ_1(kr)\end{equation}よって $G(\boldsymbol{x})$ を $r=\sqrt{x^2+y^2}$ で微分した式は、\begin{equation}\frac{dG}{dr}=-\frac{1}{2\pi}\int^\infty_0 J_1(kr)dk\end{equation}この積分を実行するために $J_0(kr)$ の $k$ 微分$$\frac{dJ_0(kr)}{dk}=-rJ_1(kr)$$を使って\begin{equation}\frac{dG}{dr}=\frac{1}{2\pi r}\bigl[ J_0(kr) \bigr]^\infty_{k=0}=\frac{1}{2\pi r}(0-1)=-\frac{1}{2\pi r}\end{equation}$$\therefore\; G(\boldsymbol{x})=-\frac{1}{2\pi}\log r$$とグリーン関数が求まります。
3次元の場合、座標を $\boldsymbol{x}=(x,y,z)$ と表せばグリーン関数 $G(\boldsymbol{x})$ が満たす微分方程式は\begin{equation}\Delta G(\boldsymbol{x})=-\delta^3(\boldsymbol{x})\tag{4}\end{equation}ここで $\delta^3(\boldsymbol{x})=\delta(x)\delta(y)\delta(z)$ です。
$G$ をフーリエ変換すれば $\boldsymbol{k}=(k_x,k_y,k_z)$ , $k^2=k_x^2+k_y^2+k_z^2$ として\begin{equation}\tilde{G}(\boldsymbol{k})=\int G(\boldsymbol{x})e^{-i\boldsymbol{k}\cdot\boldsymbol{x}}d^3x\end{equation}ここで $d^3x=dxdydz$ としています。さらに逆フーリエ変換すれば\begin{equation}G(\boldsymbol{x})=\frac{1}{8\pi^3}\int\tilde{G}(\boldsymbol{k})e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k\end{equation}となります。これにラプラシアンを作用させて\begin{eqnarray}\Delta G(\boldsymbol{x}) &=& \frac{1}{8\pi^3}\int\tilde{G}(\boldsymbol{k})\Delta e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k\\ &=&\frac{1}{8\pi^3}\int\tilde{G}(\boldsymbol{k})\left(\frac{\partial^2}{\partial x^2}+\frac{\partial^2}{\partial y^2}+\frac{\partial^2}{\partial z^2}\right) e^{i(k_xx+k_yy+k_zz)}d^3k\\&=&\frac{1}{8\pi^3}\int\tilde{G}(\boldsymbol{k})\{(ik_x)^2+(ik_y)^2+(ik_z)^2\} e^{i(k_xx+k_yy+k_zz)}d^3k\\ &=&-\frac{1}{8\pi^3}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k\end{eqnarray}このラプラシアンは $x,y,z$ に関する微分作用素なので $\boldsymbol{k}$ にはかかりません。
一方、デルタ関数 $\delta^3(\boldsymbol{x})$ のフーリエ変換は\begin{equation}\delta^3(\boldsymbol{x})=\frac{1}{8\pi^3}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k\end{equation}以上より(4)は以下のように書き換えられます。\begin{equation}-\frac{1}{8\pi^3}\int\tilde{G}(\boldsymbol{k})k^2 e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k=-\frac{1}{8\pi^3}\int e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k\end{equation}両辺を比べて\begin{equation}\tilde{G}(\boldsymbol{k})=\frac{1}{k^2}\end{equation}となります。この逆変換が求める解であり、\begin{equation}G(\boldsymbol{x})=\frac{1}{8\pi^3}\int\frac{1}{k^2}e^{i\boldsymbol{k}\cdot\boldsymbol{x}}d^3k\end{equation}となります。これは $\boldsymbol{k}$ に関して全空間にわたる積分ですので $\boldsymbol{k}$ と $\boldsymbol{x}$ のなす角を $\theta$ とすると、$\boldsymbol{x}$ を $k_z$ 軸に一致させて $\boldsymbol{k}$ の極座標表示にこの $\theta$ を用いて差し支えありません（全空間の積分値に影響しない）。すなわち$$\begin{cases}k_x&=&k\sin\theta\cos\phi\\k_y&=&k\sin\theta\sin\phi\\k_z&=&k\cos\theta\end{cases}$$$$d^3k=dk_xdk_ydk_z=k^2\sin\theta dkd\theta d\phi$$よって積分は $|\boldsymbol{x}|=r$ と表すことにして\begin{eqnarray}G(\boldsymbol{x})&=&\frac{1}{8\pi^3}\int^\infty_0dk\int^{\pi}_0d\theta\int^{2\pi}_0d\phi\: e^{ikr\cos\theta}\sin\theta\\&=& \frac{1}{4\pi^2}\int^\infty_0dk\int^{\pi}_0d\theta\: e^{ikr\cos\theta}\sin\theta\\&=& \frac{-1}{4\pi^2}\int^\infty_0dk \left[ \frac{1}{ikr} e^{ikr\cos\theta} \right]^\pi_{\theta=0}\\&=& \frac{1}{4\pi^2}\int^\infty_0\frac{e^{ikr}-e^{-ikr}}{ikr}dk\\&=& \frac{1}{2\pi^2}\int^\infty_0\frac{\sin kr}{kr}dk\\&=& \frac{1}{2\pi^2r}\int^\infty_0\frac{\sin k}{k}dk\\&=& \frac{1}{4\pi r}\end{eqnarray}$$\therefore\; G(\boldsymbol{x})=\frac{1}{4\pi |\boldsymbol{x}|}$$とグリーン関数が求まります。
3次元は物理学において応用できるので重要です。例えばマクスウェル方程式から点電荷による電位を求めるのにも使えます。
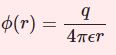マクスウェル方程式から点電荷による電位を求める
テーマに沿って、今回は１～３次元のグリーン関数について論じました。記事が長くなってきましたので4次元以上については次回に！
$$\begin{cases}G(x)&=&\displaystyle\frac{1}{2}|x|+b\\G(\boldsymbol{x})&=&- \displaystyle\frac{1}{2\pi}\log |\boldsymbol{x}|\\ G(\boldsymbol{x})&=& \displaystyle\frac{1}{4\pi |\boldsymbol{x}|}\end{cases}$$
【物理数学】N次元グリーン関数の解法(2)
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。