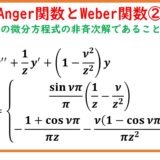
\begin{equation}I_n:=\int_{0}^{1}\arctan^n x dx\tag{1}\end{equation}とすると、$n\ge 2$ に対しては次の表式に帰着する。$$I_n=\left(\frac{\pi}{4}\right)^n+\frac{n}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2+n(n-1)\sum_{k=1}^\infty\frac{(-1)^k}{k}\int_0^\frac{\pi}{4}y^{n-2}\cos 2kydy$$残りの積分は、必要なだけ部分積分を行う。これを計算すると\begin{eqnarray*}I_2&=&\frac{\pi^2}{16}+\frac{\pi}{4}\ln 2-G\\I_3&=&\frac{63}{64}\zeta(3)-\frac{3}{4}\pi G+\frac{3}{32}\pi^2\ln2+\frac{\pi^3}{64}\\I_4&=&\frac{\pi^4}{256}+\frac{\pi^3}{32}\ln2-\frac{3}{8}\pi^2G+3\beta(4)-\frac{9}{64}\pi\zeta(3)\\I_5&=&\frac{\pi^5}{1024}+\frac{5\pi^4}{512}\ln2-\frac{5}{32}\pi^3G\\&&-\frac{45\pi^2}{512}\zeta(3)+\frac{15\pi}{4}\beta(4)-\frac{6975}{1024}\zeta(5)\end{eqnarray*}
なお $n=1$ については\begin{eqnarray*}I_1 &=& \left[x\arctan x\right]_0^1-\int_0^1\frac{xdx}{1+x^2}\\ &=&\frac{\pi}{4}-\frac{\ln 2}{2}\end{eqnarray*}と容易に計算できますが、$n\ge2$ では初等的に積分を計算できず、カタラン定数 $G$ やディリクレのベータ関数 $\beta(s)$ を使うことになります。大まかな流れについては、過去記事
x^m/(sin x)^nの積分(logsinのフーリエ展開・ディリクレのベータ関数)
と非常によく似ているので、参考になると思います。
$x=\tan y$ とおくと $dx=\dfrac{dy}{\cos^2y}$ より$$I_n=\int_0^\frac{\pi}{4}\frac{y^n}{\cos^2 y}dy$$部分積分して$$I_n=\left(\frac{\pi}{4}\right)^n-n\int_0^\frac{\pi}{4}y^{n-1}\tan y dy$$$n=1$ であれば $\tan$ の積分をして終了ですが、$n\ge 2$ なら残りの積分を部分積分して\begin{eqnarray}\int_0^\frac{\pi}{4}y^{n-1}\tan y dy &=& \left[-y^{n-1}\ln(\cos y)\right]_0^\frac{\pi}{4}+(n-1)\int_0^\frac{\pi}{4}y^{n-2}\ln(\cos y)dy\\ &=& \frac{1}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2+(n-1)\int_0^\frac{\pi}{4}y^{n-2}\ln(\cos y)dy\tag{2}\end{eqnarray}$\ln$ の中身を少々いじります。\begin{eqnarray*}\int_0^\frac{\pi}{4}y^{n-1}\tan y dy &=& \frac{1}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2\\&&+(n-1)\int_0^\frac{\pi}{4}y^{n-2}\ln(2\cos y)dy-(n-1)\ln 2\int_0^\frac{\pi}{4}y^{n-2}dy\\&=&\frac{1}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2+(n-1)\int_0^\frac{\pi}{4}y^{n-2}\ln(2\cos y)dy-\ln2\left(\frac{\pi}{4}\right)^{n-1}\\ &=& -\frac{1}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2+(n-1)\int_0^\frac{\pi}{4}y^{n-2}\ln(2\cos y)dy\end{eqnarray*}したがって$$I_n=\left(\frac{\pi}{4}\right)^n+\frac{n}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2-n(n-1)\int_0^\frac{\pi}{4}y^{n-2}\ln(2\cos y)dy$$
$\ln(2\cos2y)$ のフーリエ級数展開\begin{equation}\ln(2\cos2y)=-\sum_{n=1}^\infty\frac{(-1)^n}{n}\cos2ny\tag{3}\end{equation}を用いて次の式を得ます。
\begin{equation}I_n=\left(\frac{\pi}{4}\right)^n+\frac{n}{2}\left(\frac{\pi}{4}\right)^{n-1}\ln 2+n(n-1)\sum_{k=1}^\infty\frac{(-1)^k}{k}\int_0^\frac{\pi}{4}y^{n-2}\cos 2kydy\tag{4}\end{equation}
これの証明については
x^3/(sinx)^3の積分(ディリクレベータ関数・カタラン定数)
あとは右辺の積分を実行すればいいのですが、どうしても級数が残ってしまい、ゼータ関数やディリクレのベータ関数で処理する必要があります。ゼータ関数は有名なのでいいとして、
ディリクレのベータ関数は次の無限級数で定義される。\begin{equation}\beta(s)=\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^s}\tag{5}\end{equation}特に $\beta(2)$ をCatalan定数 $G$ とよぶ。
と押さえておきましょう。
n=2のとき
(4)より$$I_2=\frac{\pi^2}{16}+\frac{\pi}{4}\ln 2+2\sum_{k=1}^\infty\frac{(-1)^k}{k}\int_0^\frac{\pi}{4}\cos 2kydy$$残りの積分を実行して$$I_2=\frac{\pi^2}{16}+\frac{\pi}{4}\ln 2+\sum_{k=1}^\infty\frac{(-1)^k}{k^2}\sin\frac{k\pi}{2}$$級数は $k$ が偶数のときはゼロとなるので $k=2m+1$ として$$I_2=\frac{\pi^2}{16}+\frac{\pi}{4}\ln 2-\sum_{m=0}^\infty\frac{(-1)^m}{(2m+1)^2}$$ただしここで $\sin\frac{2m+1}{2}\pi=(-1)^m$ を使っています。よって
\begin{equation}\int_{0}^{1}\arctan^2 x dx=\frac{\pi^2}{16}+\frac{\pi}{4}\ln 2-G\tag{6}\end{equation}
n=3のとき
(4)より$$I_3=\frac{\pi^3}{64}+\frac{3\pi^2}{32}\ln 2+6\sum_{k=1}^\infty\frac{(-1)^k}{k}\int_0^\frac{\pi}{4}y\cos 2kydy$$残りの積分を実行して\begin{eqnarray*}I_3 &=& \frac{\pi^3}{64}+\frac{3\pi^2}{32}\ln 2+\frac{3\pi}{4}\sum_{k=1}^\infty\frac{(-1)^k}{k^2}\sin\frac{k\pi}{2}\\&&+\frac{3}{2}\sum_{k=1}^\infty\frac{(-1)^k}{k^3}\cos\frac{k\pi}{2}-\frac{3}{2}\sum_{k=1}^\infty\frac{(-1)^k}{k^3}\end{eqnarray*}$\sin\frac{k\pi}{2}$ は $k$ が偶数のときはゼロ、$\cos\frac{k\pi}{2}$ は $k$ が奇数のときはゼロとなるので、それぞれ $k=2m+1$ , $k=2m$ として和をとります。$$\sum_{k=1}^\infty\frac{(-1)^k}{k^2}\sin\frac{k\pi}{2}=-\sum_{m=0}^\infty\frac{(-1)^m}{(2m+1)^2}=-G$$$$\sum_{k=1}^\infty\frac{(-1)^k}{k^3}\cos\frac{k\pi}{2}=\frac{1}{8}\sum_{m=1}^\infty\frac{(-1)^m}{m^3}$$またゼータ関数の基本テクニック$$\sum_{k=1}^\infty\frac{(-1)^k}{k^3}=-\zeta(3)+2\frac{1}{2^3}\zeta(3)=-\frac{3}{4}\zeta(3)$$も用いて
\begin{equation}\int_{0}^{1}\arctan^3 x dx=\frac{63}{64}\zeta(3)-\frac{3}{4}\pi G+\frac{3}{32}\pi^2\ln2+\frac{\pi^3}{64}\tag{7}\end{equation}
n=4のとき
同様に進めます。積分を実行すると$$I_4=\frac{\pi^4}{256}+\frac{\pi^3}{32}\ln2+3\sum_{k=1}^\infty\frac{(-1)^k}{k}\left[\frac{\pi^2\sin\frac{k\pi}{2}}{8k}+\frac{\pi\cos\frac{k\pi}{2}}{2k^2}-\frac{\sin\frac{k\pi}{2}}{k^3}\right]$$これまでと同じく$$\sum_{k=1}^\infty\frac{(-1)^k\sin\frac{k\pi}{2}}{k^2}=-\sum_{m=0}^\infty\frac{(-1)^m}{(2m+1)^2}=-G$$$$\sum_{k=1}^\infty\frac{(-1)^k\cos\frac{k\pi}{2}}{k^3}=\sum_{m=0}^\infty\frac{(-1)^m}{8m^3}=-\frac{3}{32}\zeta(3)$$$$\sum_{k=1}^\infty\frac{(-1)^k\sin\frac{k\pi}{2}}{k^4}=-\sum_{m=0}^\infty\frac{(-1)^m}{(2m+1)^4}=-\beta(4)$$したがって
\begin{equation}\int_{0}^{1}\arctan^4 x dx=\frac{\pi^4}{256}+\frac{\pi^3}{32}\ln2-\frac{3}{8}\pi^2G+3\beta(4)-\frac{9}{64}\pi\zeta(3)\tag{8}\end{equation}
n=5のとき
不定積分は$$\int y^3\cos 2kydy=\frac{y^3\sin2ky}{2k}+\frac{3y^2\cos2ky}{4k^2}-\frac{3y\sin2ky}{4k^3}-\frac{3\cos2ky}{8k^4}$$です。ゴリゴリ計算して
\begin{eqnarray}\int_{0}^{1}\arctan^5 x dx &=& \frac{\pi^5}{1024}+\frac{5\pi^4}{512}\ln2-\frac{5}{32}\pi^3G\\&&-\frac{45\pi^2}{512}\zeta(3)+\frac{15\pi}{4}\beta(4)-\frac{6975}{1024}\zeta(5)\tag{9}\end{eqnarray}

音のうなり

ヤコビの楕円関数4~周期を2倍にする・ペー関数との関係

テータ関数11~ヤコビの楕円関数の登場

大気圧と水圧の体感実習
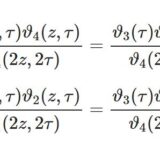
テータ関数10~ランデン変換と微分方程式
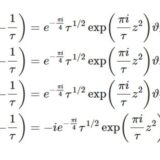
テータ関数9~ヤコビの虚数変換式

初等整数問題①~下1桁の考察
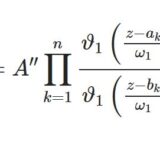
テータ関数8~ワイエルシュトラスのシグマ・ゼータ関数や楕円関数との関係
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。