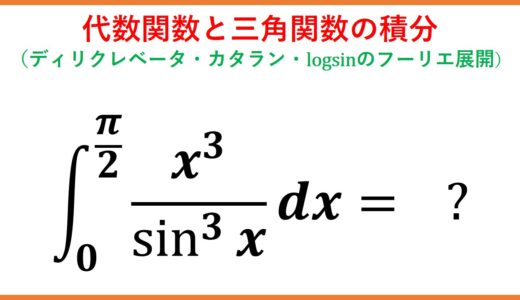自然数 $m\ge n$ に対し、$$\int_0^\frac{\pi}{2}\frac{x^m}{\sin^n x}dx$$を考える。おそらく $m=n=2$ のとき以外は初等的に計算できず、奇数ゼータ $\zeta(3),\zeta(5),\cdots$ や偶数のディリクレベータ関数 $\beta(2),\beta(4),\cdots$ の組み合わせで表される。
これまでに計算したものは以下である。\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x}{\sin x}dx&=&2G\\\int_0^\frac{\pi}{2}\frac{x^2}{\sin x}dx&=&2\pi G-\frac{7}{2}\zeta(3)\\\int_0^\frac{\pi}{2}\frac{x^3}{\sin x}dx&=&\frac{3}{2}\pi^2 G-12\beta(4)\\\int_0^\frac{\pi}{2}\frac{x^4}{\sin x}dx&=&\pi^3 G-24\pi\beta(4)+\frac{93}{2}\zeta(5)\end{eqnarray*}
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^2}{\sin^2 x}dx&=&\pi\ln2\\\int_0^\frac{\pi}{2}\frac{x^3}{\sin^2 x}dx&=&\frac{3}{4}\pi^2\ln2-\frac{21}{8}\zeta(3)\\\int_0^\frac{\pi}{2}\frac{x^4}{\sin^2 x}dx&=&\frac{\pi^3}{2}\ln2-\frac{9}{4}\pi\zeta(3)\\\int_0^\frac{\pi}{2}\frac{x^5}{\sin^2 x}dx&=&\frac{5}{16}\pi^4\ln2-\frac{45}{16}\pi^2\zeta(3)+\frac{465}{32}\zeta(5)\end{eqnarray*}
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3 x}dx&=&-\frac{3}{8}\pi^2+\left(6+\frac{3}{4}\pi^2\right)G-6\beta(4)\\\int_0^\frac{\pi}{2}\frac{x^4}{\sin^3 x}dx&=&-\frac{\pi^3}{4}-21\zeta(3)+\frac{93}{4}\zeta(5)+\left(\frac{\pi^3}{2}+12\pi\right)G-12\pi\beta(4)\end{eqnarray*}
$$\int_0^\frac{\pi}{2}\frac{x^4}{\sin^4 x}dx=-\frac{\pi^3}{12}+\left(2+\frac{\pi^2}{3}\right)\pi\ln2-\frac{3}{2}\pi\zeta(3)$$
ここで $G\equiv\beta(2)$ をカタラン定数という。
これらの導出方法は、おおまかには共通していますので、過去記事も参考にしてください:
上記の積分は、まず $x^m$ と $\sin^{-n}x$ に分けて部分積分をします。その際、後者を積分して前者を微分することにより $x$ の次数を下げるのです。$\sin^{-n}x$ の不定積分は $n$ によって結構変わってきますので、それ以降はケースバイケースで進めます。
道中で $\ln\sin$ や $\ln\cos$ および $\ln\tan$ の積分が現れることがあります。この場合はそれらをフーリエ級数展開することでうまく進めることができます。
本題に入る前に、いくらか準備が必要です。
ディリクレのベータ関数は次の無限級数で定義される。\begin{equation}\beta(s)=\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^s}\tag{1}\end{equation}特に $\beta(2)$ をCatalan定数 $G$ とよぶ。
本稿で多用するので覚えておきましょう。
まだ準備は続きます。
$n\ge 2$ のとき $S_n=\displaystyle\int\frac{dx}{\sin^n x}$ とすると\begin{equation}(n-1)S_n=(n-2)S_{n-2}-\frac{\cos x}{\sin^{n-1}x}\tag{2}\end{equation}
【証明】部分積分によります。\begin{eqnarray*}S_n&&=\int\frac{1}{\sin^2x}\frac{dx}{\sin^{n-2} x}\\&&=-\frac{\cos x}{\sin^{n-1}x}-(n-2)\int\frac{\cos^2x}{\sin^nx}dx\\&&=-\frac{\cos x}{\sin^{n-1}x}-(n-2)(S_n-S_{n-2})\end{eqnarray*}【証明終】
$0\le x\le \frac{\pi}{2}$ とすると $\csc^nx$ の不定積分は以下のようになる。積分定数は省略する。\begin{equation}\begin{cases}\displaystyle\int\frac{dx}{\sin x}&=&\ln\tan\frac{x}{2}\\\displaystyle\int\dfrac{dx}{\sin^2 x}&=&-\dfrac{\cos x}{\sin x}=-\cot x\\\displaystyle\int\dfrac{dx}{\sin^3 x}&=&\dfrac{1}{2}\left(\ln\tan\dfrac{x}{2}-\dfrac{\cos x}{\sin^2x}\right)\\\displaystyle\int\dfrac{dx}{\sin^4 x}&=&-\dfrac{1}{3}\left(\dfrac{\cos x}{\sin^3 x}+2\dfrac{\cos x}{\sin x}\right)\end{cases}\tag{3}\end{equation}
【証明】補題1を使うもよし、うまく置換して計算してもよしです。\begin{eqnarray*}\int\frac{dx}{\sin x}&&=\int\frac{\sin xdx}{1-\cos^2x}\\&&=-\frac{1}{2}\int\left(\frac{1}{1-\cos x}+\frac{1}{1+\cos x}\right)d(\cos x)\\&&=\frac{1}{2}\ln\frac{1-\cos x}{1+\cos x}\\&&=\ln\tan\frac{x}{2}\end{eqnarray*}次に$$\int\frac{dx}{\sin^2 x}=-\cot x$$は覚えていていいレベルです。次は補題を使いましょう\begin{eqnarray*}\int\frac{dx}{\sin^3 x}&&=\frac{1}{2}\left(\int\frac{dx}{\sin x}-\frac{\cos x}{\sin^2x}\right)\\&&=\frac{1}{2}\left(\ln\tan\frac{x}{2}-\frac{\cos x}{\sin^2x}\right)\end{eqnarray*}以下同様です。\begin{eqnarray*}\int\frac{dx}{\sin^4 x}&&=\frac{1}{3}\left(\int\frac{dx}{\sin^2 x}-\frac{\cos x}{\sin^3x}\right)\\&&=\frac{1}{3}\left(-\frac{\cos x}{\sin x}-\frac{\cos x}{\sin^3x}\right)\\&&=-\frac{1}{3}\left(\frac{\cos x}{\sin^3 x}+2\frac{\cos x}{\sin x}\right)\end{eqnarray*}【証明終】
$0<x<\frac{\pi}{2}$ において\begin{equation}\ln(2\sin x)=-\sum_{n=1}^\infty\frac{\cos 2nx}{n}\tag{4}\end{equation}\begin{equation}\ln(2\cos x)=\sum_{n=1}^\infty\frac{(-1)^{n-1}\cos 2nx}{n}\tag{5}\end{equation}\begin{equation}\ln\tan x=-2\sum_{n=0}^\infty\frac{\cos2(2n+1)x}{2n+1}\tag{6}\end{equation}
式の形より、それぞれ左辺のフーリエ展開を表しています。
【証明】対数のマクローリン展開$$\ln(1-X)=-X-\frac{X^2}{2}-\frac{X^3}{3}-\cdots$$を用います。\begin{eqnarray*}\ln(2\sin x)&&=\ln (e^{i(x-\frac{\pi}{2})}-e^{i(-x-\frac{\pi}{2})})\\&&=\left(x-\frac{\pi}{2}\right)i+\ln\left(1-e^{-2ix}\right)\\&&=\left(x-\frac{\pi}{2}\right)i-\sum_{n=1}^\infty\frac{(e^{-2ix})^n}{n}\\&&=\left(x-\frac{\pi}{2}+\sum_{n=1}^\infty\frac{\sin 2nx}{n}\right)i-\sum_{n=1}^\infty\frac{\cos2nx}{n}\end{eqnarray*}実部をとれば(4)が成立します。
次に\begin{eqnarray*}\ln(2\cos x)&&=\ln(e^{ix}+e^{-ix})\\&&=ix+\ln(1+e^{-2ix})\\&&=ix+\sum_{n=1}^\infty\frac{(-1)^{n-1}(e^{-2ix})^n}{n}\\&&=ix+\sum_{n=1}^\infty\frac{(-1)^{n-1}e^{-2inx}}{n}\\&&=i\left(x+\sum_{n=1}^\infty\frac{(-1)^n\sin2nx}{n}\right)+\sum_{n=1}^\infty\frac{(-1)^{n-1}\cos 2nx}{n}\end{eqnarray*}実部をとれば(5)を得ます。
最後に、(4)(5)を辺々引いて\begin{eqnarray*}\ln\tan x&&=-\sum_{n=1}^\infty\left(\frac{\cos 2nx}{n}+\frac{(-1)^{n-1}\cos 2nx}{n}\right)\\&&=\sum_{n=1}^\infty\left\{(-1)^n-1\right\}\frac{\cos2nx}{n}\end{eqnarray*}$n$ を偶奇で分けましょう。$n$ を $2n+1$ および $2n$ に書き換えると\begin{eqnarray*}\ln\tan x&&=\sum_{n=0}^\infty\left\{(-1)^{2n+1}-1\right\}\frac{\cos2(2n+1)x}{2n+1}+\sum_{n=1}^\infty\left\{(-1)^{2n}-1\right\}\frac{\cos4nx}{2n}\\&&=-2\sum_{n=0}^\infty\frac{\cos2(2n+1)x}{2n+1}\end{eqnarray*}【証明終】
これで準備は終わりです!では計算していきましょう。
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x}{\sin x}dx&=&2G\\\int_0^\frac{\pi}{2}\frac{x^2}{\sin x}dx&=&2\pi G-\frac{7}{2}\zeta(3)\\\int_0^\frac{\pi}{2}\frac{x^3}{\sin x}dx&=&\frac{3}{2}\pi^2 G-12\beta(4)\\\int_0^\frac{\pi}{2}\frac{x^4}{\sin x}dx&=&\pi^3 G-24\pi\beta(4)+\frac{93}{2}\zeta(5)\end{eqnarray*}
【証明】まずは\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x}{\sin x}dx&&=2\int_0^1\frac{\arctan y}{y}dy\quad(y=\tan\frac{x}{2})\\&&=2\int_0^1\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}y^{2n}dy\\&&=2\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}\\&&=2G\end{eqnarray*}
次に2乗です。ここからは定理1を用いた部分積分でスタートし、道中で定理2を利用します。\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^2}{\sin x}dx&&=\left[x^2\ln\tan\frac{x}{2}\right]_0^\frac{\pi}{2}-2\int_0^\frac{\pi}{2}x\ln\tan\frac{x}{2}dx\\&&=-8\int_0^\frac{\pi}{4}x\ln\tan xdx\\&&=16\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}x\cos2(2n+1)xdx\quad(\because(6))\\&&=16\sum_{n=0}^\infty\frac{1}{2n+1}\left(\frac{\pi(-1)^n}{8(2n+1)}-\frac{1}{4(2n+1)^2}\right)\\&&=2\pi G-4\sum_{n=0}^\infty\frac{1}{(2n+1)^3}\\&&=2\pi G-\frac{7}{2}\zeta(3)\end{eqnarray*}
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^3}{\sin x}dx&&=\left[x^3\ln\tan\frac{x}{2}\right]_0^\frac{\pi}{2}-3\int_0^\frac{\pi}{2}x^2\ln\tan\frac{x}{2}dx\\&&=48\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}x^2\cos2(2n+1)xdx\\&&=48\sum_{n=0}^\infty\frac{1}{2n+1}\left(\frac{\pi^2(-1)^n}{32(2n+1)}-\frac{(-1)^n}{4(2n+1)^3}\right)\\&&=\frac{3}{2}\pi^2G-12\beta(4)\end{eqnarray*}
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^4}{\sin x}dx&&=\left[x^4\ln\tan\frac{x}{2}\right]_0^\frac{\pi}{2}-4\int_0^\frac{\pi}{2}x^3\ln\tan\frac{x}{2}dx\\&&=128\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}x^3\cos2(2n+1)xdx\\&&=128\sum_{n=0}^\infty\frac{1}{2n+1}\left(\frac{\pi^3(-1)^n}{128(2n+1)}-\frac{3\pi(-1)^n}{16(2n+1)^3}+\frac{3}{8(2n+1)^4}\right)\\&&=\pi^3G-24\pi\beta(4)+\frac{93}{2}\zeta(5)\end{eqnarray*}【証明終】
以上で定理3は示されました。本日の結論の1つめです。
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^2}{\sin^2 x}dx&=&\pi\ln2\\\int_0^\frac{\pi}{2}\frac{x^3}{\sin^2 x}dx&=&\frac{3}{4}\pi^2\ln2-\frac{21}{8}\zeta(3)\\\int_0^\frac{\pi}{2}\frac{x^4}{\sin^2 x}dx&=&\frac{\pi^3}{2}\ln2-\frac{9}{4}\pi\zeta(3)\\\int_0^\frac{\pi}{2}\frac{x^5}{\sin^2 x}dx&=&\frac{5}{16}\pi^4\ln2-\frac{45}{16}\pi^2\zeta(3)+\frac{465}{32}\zeta(5)\end{eqnarray*}
【証明】定理1による部分積分をしましょう。まずは\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^2}{\sin^2 x}dx&&=\left[-x^2\cot x\right]_0^\frac{\pi}{2}+\int_0^\frac{\pi}{2}2x\cot xdx\\&&=2\int_0^\frac{\pi}{2}x\cot xdx\\&&=\left[2x\ln\sin x\right]_0^\frac{\pi}{2}-2\int_0^\frac{\pi}{2}\ln\sin xdx\\&&=-2\int_0^\frac{\pi}{2}\ln\sin xdx\\&&=\pi\ln2\end{eqnarray*}最後の等号については、初等的に計算できますので次の記事を参考にしてください:
3乗以降は次のように計算します。定理2も使います。\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^3}{\sin^2 x}dx&&=\left[-x^3\cot x\right]_0^\frac{\pi}{2}+3\int_0^\frac{\pi}{2}x^2\cot xdx\\&&=3\int_0^\frac{\pi}{2}x^2\cot xdx\\&&=\left[3x^2\ln\sin x\right]_0^\frac{\pi}{2}-6\int_0^\frac{\pi}{2}x\ln\sin xdx\\&&=-6\int_0^\frac{\pi}{2}x\ln\sin xdx\\&&=6\int_0^\frac{\pi}{2}x(\ln2-\ln2\sin x)dx\\&&=\frac{3}{4}\pi^2\ln2+6\sum_{n=1}^\infty\frac{1}{n}\int_0^\frac{\pi}{2}x\cos2nxdx\\&&=\frac{3}{4}\pi^2\ln2+6\sum_{n=1}^\infty\frac{(-1)^n-1}{4n^3}\\&&=\frac{3}{4}\pi^2\ln2-3\sum_{n=0}^\infty\frac{1}{(2n+1)^3}\\&&=\frac{3}{4}\pi^2\ln2-\frac{21}{8}\zeta(3)\end{eqnarray*}
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^4}{\sin^2 x}dx&&=\left[-x^4\cot x\right]_0^\frac{\pi}{2}+4\int_0^\frac{\pi}{2}x^3\cot xdx\\&&=\left[4x^3\ln\sin x\right]_0^\frac{\pi}{2}-12\int_0^\frac{\pi}{2}x^2\ln\sin xdx\\&&=12\int_0^\frac{\pi}{2}x^2[\ln2-\ln(2\sin x)]dx\\&&=\frac{\pi^3}{2}\ln2+12\sum_{n=1}^\infty\frac{1}{n}\int_0^\frac{\pi}{2}x^2\cos2nxdx\\&&=\frac{\pi^3}{2}\ln2+12\sum_{n=1}^\infty\frac{1}{n}\frac{\pi(-1)^n}{4n^2}\\&&=\frac{\pi^3}{2}\ln2-3\pi\frac{3}{4}\zeta(3)\\&&=\frac{\pi^3}{2}\ln2-\frac{9}{4}\pi\zeta(3)\end{eqnarray*}
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^5}{\sin^2 x}dx&&=\frac{5\pi^4}{16}\ln2+20\sum_{n=1}^\infty\frac{1}{n}\int_0^\frac{\pi}{2}x^3\cos2nxdx\\&&=\frac{5\pi^4}{16}\ln2+20\sum_{n=1}^\infty\frac{1}{n}\left(\frac{3\pi^2(-1)^n}{16n^2}-\frac{3(-1)^n}{8n^4}+\frac{3}{8n^4}\right)\\&&=\frac{5}{16}\pi^4\ln2-\frac{45}{16}\pi^2\zeta(3)+\frac{465}{32}\zeta(5)\end{eqnarray*}【証明終】
以上が本日の結論2つめです。
\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3 x}dx&=&-\frac{3}{8}\pi^2+\left(6+\frac{3}{4}\pi^2\right)G-6\beta(4)\\\int_0^\frac{\pi}{2}\frac{x^4}{\sin^3 x}dx&=&-\frac{\pi^3}{4}-21\zeta(3)+\frac{93}{4}\zeta(5)+\left(\frac{\pi^3}{2}+12\pi\right)G-12\pi\beta(4)\end{eqnarray*}
【証明】定理1による部分積分をしましょう。\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3 x}dx&&=\left[\frac{x^3}{2}\left(\ln\tan\frac{x}{2}-\frac{\cos x}{\sin^2x}\right)\right]_0^\frac{\pi}{2}-\frac{3}{2}\int_0^\frac{\pi}{2}x^2\left(\ln\tan\frac{x}{2}-\frac{\cos x}{\sin^2x}\right)dx\\&&=\frac{3}{2}\int_0^\frac{\pi}{2}x^2\left(\frac{\cos x}{\sin^2x}-\ln\tan\frac{x}{2}\right)dx\end{eqnarray*}右辺第1項は\begin{eqnarray*}\int_0^\frac{\pi}{2}x^2\frac{\cos x}{\sin^2x}dx&&=\left[-\frac{x^2}{\sin x}\right]_0^\frac{\pi}{2}+2\int_0^\frac{\pi}{2}\frac{x}{\sin x}dx\\&&=-\frac{\pi^2}{4}+4G\end{eqnarray*}第2項は $\frac{x}{2}\to y$ と置換します。\begin{eqnarray*}\int_0^\frac{\pi}{2}x^2\ln\tan\frac{x}{2}dx&&=-16\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}y^2\cos2(2n+1)ydy\\&&=-16\sum_{n=0}^\infty\left(\frac{\pi^2(-1)^n}{32(2n+1)^2}-\frac{(-1)^n}{4(2n+1)^4}\right)\\&&=-\frac{\pi^2}{2}G+4\beta(4)\end{eqnarray*}以上より$$\int_0^\frac{\pi}{2}\frac{x^3}{\sin^3x}dx=-\frac{3}{8}\pi^2+\left(6+\frac{3}{4}\pi^2\right)G-6\beta(4)$$
次いきます。定理1を用いた部分積分により\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^4}{\sin^3 x}dx&&=2\int_0^\frac{\pi}{2}x^3\left(\frac{\cos x}{\sin^2x}-\ln\tan\frac{x}{2}\right)dx\\&&=2\left(-\frac{\pi^3}{8}+3\int_0^\frac{\pi}{2}\frac{x^2dx}{\sin^2x}\right)-32\int_0^\frac{\pi}{4}x^3\ln\tan xdx\\&&=-\frac{\pi^3}{4}+12\pi G-21\zeta(3)-32\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}x^3\ln\tan xdx\\&&=-\frac{\pi^3}{4}+12\pi G-21\zeta(3)+64\sum_{n=0}^\infty\frac{1}{2n+1}\int_0^\frac{\pi}{4}x^3\cos2(2n+1)xdx\\&&-\frac{\pi^3}{4}+12\pi G-21\zeta(3)+64\sum_{n=0}^\infty\left(\frac{\pi^3(-1)^n}{128(2n+1)^2}-\frac{3\pi(-1)^n}{16(2n+1)^4}+\frac{3}{8(2n+1)^5}\right)\\&&=-\frac{\pi^3}{4}-21\zeta(3)+\frac{93}{4}\zeta(5)+\left(\frac{\pi^3}{2}+12\pi\right)G-12\pi\beta(4)\end{eqnarray*}【証明終】
これで3つめの結論を得ました。
$$\int_0^\frac{\pi}{2}\frac{x^4}{\sin^4 x}dx=-\frac{\pi^3}{12}+\left(2+\frac{\pi^2}{3}\right)\pi\ln2-\frac{3}{2}\pi\zeta(3)$$
【証明】\begin{eqnarray*}\int_0^\frac{\pi}{2}\frac{x^4}{\sin^4 x}dx&&=\frac{4}{3}\int_0^\frac{\pi}{2}x^3\left(\frac{1}{\sin^3x}+\frac{2}{\sin x}\right)\cos xdx\\&&=-\frac{\pi^3}{12}+2\int_0^\frac{\pi}{2}\frac{x^2dx}{\sin^2x}-8\int_0^\frac{\pi}{2}x^2\ln\sin xdx\\&&=-\frac{\pi^3}{12}+2\pi\ln2-8\int_0^\frac{\pi}{2}x^2[\ln(2\sin x)-\ln2]dx\\&&=-\frac{\pi^3}{12}+2\pi\ln2+\frac{\pi^3}{3}\ln2+8\sum_{n=1}^\infty\frac{1}{n}\int_0^\frac{\pi}{2}x^2\cos 2nxdx\\&&=-\frac{\pi^3}{12}+2\pi\ln2+\frac{\pi^3}{3}\ln2+2\pi\sum_{n=1}^\infty\frac{(-1)^n}{n^3}\\&&=-\frac{\pi^3}{12}+\left(2+\frac{\pi^2}{3}\right)\pi\ln2-\frac{3}{2}\pi\zeta(3)\end{eqnarray*}【証明終】
$m$ や $n$ が偶数だと少し式が簡単になる傾向がある???
これで冒頭のテーマで挙げた式すべてを導出できました!
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。