重積分\begin{equation}I\equiv\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}=\frac{\pi^2}{8}\tag{1}\end{equation}を利用して次の定積分が成立することを示す。
\begin{equation}\int_0^\infty[\mathrm{arcsinh}(\cosh x)-x]dx=\frac{\pi^2}{16}\tag{2}\end{equation}\begin{equation}\int_{\ln(1+\sqrt{2})}^\infty[x-\mathrm{arcosh}(\sinh x)]dx=\frac{\pi^2}{16}-\frac{1}{2}\ln^2(1+\sqrt{2})\tag{3}\end{equation}\begin{equation}\int_{\frac{1}{2}\ln(1+\sqrt{2})}^\infty\log\tanh xdx=\frac{\ln^2(1+\sqrt{2})}{4}-\frac{\pi^2}{16}\tag{4}\end{equation}
(1)の重積分については過去記事でも扱っています:
本記事で参考にした論文はこちら:
$I$ を級数展開するとゼータ関数が現れ、ただちに(1)式が示されます。\begin{eqnarray*}I&&=\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}\\&&=\int_0^1\left(\int_0^1(1+x^2y^2+x^4y^4+\cdots)dx\right)dy\\&&=\int_0^1\left[x+\frac{x^3}{3}y^2+\frac{x^5}{5}y^4+\frac{x^7}{7}y^6+\cdots\right]_{x=0}^1dy\\&&=\int_0^1\left(1+\frac{1}{3}y^2+\frac{1}{5}y^4+\cdots\right)dy\\&&=\left[y+\frac{y^3}{3^2}+\frac{y^5}{5^2}+\frac{y^7}{7^2}\cdots\right]_0^1\\&&=\sum_{n=1}^\infty\frac{1}{(2n+1)^2}\\&&=\sum_{n=1}^\infty\frac{1}{n^2}-\sum_{n=1}^\infty\frac{1}{(2n)^2}\\&&=\frac{3}{4}\sum_{n=1}^\infty\frac{1}{n^2}=\frac{3}{4}\zeta(2)\\&&=\frac{\pi^2}{8}\end{eqnarray*}
\begin{equation}I=\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}=\frac{\pi^2}{8}\tag{5}\end{equation}
(1)式において\begin{equation}x=\frac{\sinh u}{\cosh v}\quad,\quad y=\frac{\sinh v}{\cosh u}\quad(u,v\ge0)\tag{6}\end{equation}と置換します。このときヤコビアンは\begin{eqnarray*}\left|\begin{matrix}\frac{\cosh u}{\cosh v}&&-\frac{\sinh u\sinh v}{\cosh^2v}\\-\frac{\sinh v \sinh u}{\cosh^2 u}&&\frac{\cosh v}{\cosh u}\end{matrix}\right|&&=1-\frac{\sinh^2u\sinh^2v}{\cosh^2u\cosh^2v}\\&&=1-x^2y^2\end{eqnarray*}なので、$$I=\int_0^1\int_0^1\frac{dxdy}{1-x^2y^2}=\iint_Ddudv$$ここで領域 $D$ は $(u,v)$ の積分範囲です。すなわち $I$ は $uv$ 座標における $D$ の面積に等しいことになります。(5)と合わせれば
\begin{equation}\iint_Ddudv=\frac{\pi^2}{8}\tag{7}\end{equation}
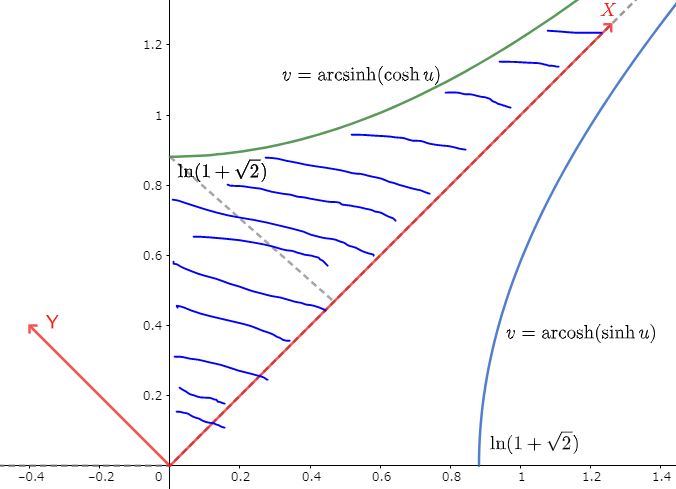
では $D$ はどのような範囲か。$0\le x\le1$ および $0\le y\le1$ でしたから(6)より$$0\le\sinh u\le\cosh v\quad,\quad 0\le\sinh v\le\cosh u$$これを整理すると\begin{equation}\begin{cases}0\le v\le\mathrm{arcsinh}(\cosh u)\\0\le u\le\mathrm{arcsinh}(\cosh v)\end{cases}\tag{8}\end{equation}となり、下図で示されます。

上図で表される領域 $D$ は 点線 $v=u$ に関して対称です。よって $D$ の面積は上半分を計算して2倍すればいいです。(7)より\begin{eqnarray*}\frac{\pi^2}{8}&&=\iint_Ddudv\\&&=2\int_0^\infty\left(\int_{u}^{\mathrm{arcsinh}(\cosh u)} dv\right)du\\&&=2\int_0^\infty\left(\mathrm{arcsinh}(\cosh u)-u\right)du\end{eqnarray*}
これにより冒頭の(2)式が示されました。
\begin{equation}\int_0^\infty[\mathrm{arcsinh}(\cosh x)-x]dx=\frac{\pi^2}{16}\tag{9}\end{equation}
今度は逆に先ほどの図の下半分を計算して2倍しましょう。\begin{eqnarray*}\frac{\pi^2}{8}&&=\iint_Ddudv\\&&=2\left[\frac{1}{2}\ln^2(1+\sqrt{2})+\int_{\ln(1+\sqrt{2})}^\infty\left(\int_{\mathrm{arcosh}(\sinh u)}^u dv\right)du\right]\\&&=\ln^2(1+\sqrt{2})+2\int_{\ln(1+\sqrt{2})}^\infty[u-\mathrm{arcosh}(\sinh u)]du\end{eqnarray*}
これにより冒頭の(3)式が示されました。
\begin{equation}\int_{\ln(1+\sqrt{2})}^\infty[x-\mathrm{arcosh}(\sinh x)]dx=\frac{\pi^2}{16}-\frac{1}{2}\ln^2(1+\sqrt{2})\tag{10}\end{equation}
領域の上半分を用いて(9)を導出したときの式に戻ります。\begin{equation}\frac{\pi^2}{8}=2\int_0^\infty\left(\int_{u}^{\mathrm{arcsinh}(\cosh u)} dv\right)du\tag{11}\end{equation}
$u,v$ 軸を $\frac{\pi}{4}$ 回転させて $X,Y$ 軸をとります。このとき座標変換の式は\begin{equation}u=\frac{X-Y}{\sqrt{2}}\quad,\quad v=\frac{X+Y}{\sqrt{2}}\tag{12}\end{equation}であり、新しい座標軸 $XY$ は下図のようになります。
(12)のヤコビアンは $J=1$ ですので $dXdY=dudv$ です。
上の網掛け部分の面積を $XY$ 座標で求めましょう。直角二等辺三角形と緑の曲線部分に分かれます。緑の曲線 $v=\mathrm{arcsinh}(\cosh u)$ を $X,Y$ に変換すると\begin{eqnarray*}&&\frac{X+Y}{\sqrt{2}}=\mathrm{arcsinh}\cosh\frac{X-Y}{\sqrt{2}}\\&&\Rightarrow \sinh\frac{X+Y}{\sqrt{2}}=\cosh\frac{X-Y}{\sqrt{2}}\\&&\Rightarrow\cosh\frac{Y}{\sqrt{2}}\left(\sinh\frac{X}{\sqrt{2}}-\cosh\frac{X}{\sqrt{2}}\right)=-\sinh\frac{Y}{\sqrt{2}}\left(\sinh\frac{X}{\sqrt{2}}+\cosh\frac{X}{\sqrt{2}}\right)\\&&\Rightarrow \tanh\frac{Y}{\sqrt{2}}=\frac{1-\tanh\frac{X}{\sqrt{2}}}{1+\tanh\frac{X}{\sqrt{2}}}\\&&\Rightarrow Y=\sqrt{2}\mathrm{arctanh}\frac{1-\tanh\frac{X}{\sqrt{2}}}{1+\tanh\frac{X}{\sqrt{2}}}\end{eqnarray*}とても複雑に見えますが$$\mathrm{arctanh}x=\frac{1}{2}\ln\frac{1+x}{1-x}$$なる公式を使えば$$Y=-\frac{1}{\sqrt{2}}\ln\tanh\frac{X}{\sqrt{2}}$$これが緑の曲線の式です。したがって(11)は\begin{eqnarray*}\frac{\pi^2}{16}&&=\int_0^\infty\left(\int_{u}^{\mathrm{arcsinh}(\cosh u)} dv\right)du\\&&=\frac{1}{2}\left(\frac{\ln(1+\sqrt{2})}{\sqrt{2}}\right)^2+\int_{\frac{\ln(1+\sqrt{2})}{\sqrt{2}}}^\infty\left(\int_0^{-\frac{1}{\sqrt{2}}\ln\tanh\frac{X}{\sqrt{2}}}dY\right)dX\\&&=\frac{\ln^2(1+\sqrt{2})}{4}-\frac{1}{\sqrt{2}}\int_{\frac{\ln(1+\sqrt{2})}{\sqrt{2}}}^\infty\ln\tanh\frac{X}{\sqrt{2}}dX\\&&=\frac{\ln^2(1+\sqrt{2})}{4}-\int_\frac{\ln(1+\sqrt{2})}{2}^\infty\ln\tanh xdx\quad(x=\frac{X}{\sqrt{2}})\end{eqnarray*}
これで冒頭の(4)式が証明できました。
\begin{equation}\int_{\frac{1}{2}\ln(1+\sqrt{2})}^\infty\log\tanh xdx=\frac{\ln^2(1+\sqrt{2})}{4}-\frac{\pi^2}{16}\tag{13}\end{equation}
この結果を応用した記事はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。




