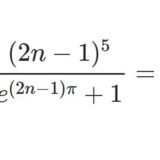ワイエルシュトラスのペー関数を使って以下の式を導出する。\begin{align}\cfrac{\displaystyle\int_2^{17}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_2^{3}\cfrac{dx}{\sqrt{x^3-7x+6}}}&=2\\[1em]\cfrac{\displaystyle\int_2^{842}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_2^{4}\cfrac{dx}{\sqrt{x^3-7x+6}}}&=2\\[1em]\cfrac{\displaystyle\int_2^{122}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_5^{\infty}\cfrac{dx}{\sqrt{x^3-7x+6}}}&=2\\[1em]\cfrac{\displaystyle\int_2^{17}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_7^{\infty}\cfrac{dx}{\sqrt{x^3-7x+6}}}&=2\\[1em]\cfrac{\displaystyle\int_2^{3}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_2^{7-5\sqrt{2}+2\sqrt{15}-\sqrt{30}}\cfrac{dx}{\sqrt{x^3-7x+6}}}&=2\end{align}
右辺が「2」ばかりなのは、ワイエルシュトラスのペー関数の「2倍」公式を応用したからです。積分はすべて実軸上で行います。なお一番上の式はこちらで初等的にも導出してます。
すべてに共通する被積分関数は$$x^3-7x+6=(x-1)(x-2)(x+3)$$であり、$x\ge 2$ に含まれる範囲なら積分できます。ただし根号の中に三次式が入っているためこれは楕円積分であり、初等的に計算できません。
冒頭の第1式を例に考えます。\begin{equation}I=\int_2^{3}\cfrac{dx}{\sqrt{x^3-7x+6}}\;,\quad J=\int_2^{17}\cfrac{dx}{\sqrt{x^3-7x+6}}\tag{1}\end{equation}とおいて $x\to 4x$ と置換すると\begin{equation}I=\int_{1/2}^{3/4}\frac{dx}{\sqrt{4x^3-\frac{7}{4}x+\frac{3}{8}}}\;,\quad J=\int_{1/2}^{17/4}\frac{dx}{\sqrt{4x^3-\frac{7}{4}x+\frac{3}{8}}}\tag{2}\end{equation}ワイエルシュトラスのペー関数の形を思い起こすと不変量は\begin{equation}g_2=\frac{7}{4}\;,\quad g_3=-\frac{3}{8}\tag{3}\end{equation}であり、3次方程式の簡単な計算から\begin{equation}e_1=\frac{1}{2}\;,\; e_2=\frac{1}{4}\;,\; e_3=-\frac{3}{4}\tag{4}\end{equation}なので(2)は\begin{equation}I=\int_{e_1}^{a}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\;,\quad J=\int_{e_1}^{b}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\tag{5}\end{equation}の形に整理できます$(e_1<a<b)$。本日の公式はすべて(5)の形からスタートします。
また積分区間に注目すれば\begin{equation}I=I_1-I_2\;,\quad J=I_1-J_2\tag{6}\end{equation}と書けます。ただし\begin{align}I_1 &=\int_{e_1}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\tag{7a}\\I_2 &=\int_{a}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\tag{7b}\\J_2 &=\int_{b}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\tag{7c}\end{align}今回の不変量は(3)で与えられているため、周期の1つ $\o_1$ は実数であり、\begin{equation}\frac{\o_1}{2} =\int_{e_1}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\tag{8}\end{equation}と書けます。これは(7a)に一致することから(というか今回の積分は全てそうなるように設定した)\begin{equation}I=\frac{\o_1}{2}-I_2\;,\quad J=\frac{\o_1}{2}-J_2\tag{9}\end{equation}大小関係は明らかに\begin{equation}0<J_2<I_2<\frac{\o_1}{2}\tag{10}\end{equation}ペー関数の表示から\begin{equation}\wp\left(\frac{\o_1}{2}\right)=e_1\;,\;\wp(I_2)=a\;,\;\wp(J_2)=b\tag{11}\end{equation}
(9)の各式において両辺のペー関数をとると\begin{equation}\wp(I)=\wp\left(\frac{\o_1}{2}-I_2\right)\;,\;\wp(J)=\wp\left(\frac{\o_1}{2}-J_2\right)\tag{12}\end{equation}ここで導出した加法定理によって\begin{equation}\wp\left(\frac{\o_1}{2}-z\right)=e_1+\frac{(e_1-e_2)(e_1-e_3)}{\wp(z)-e_1}\tag{13}\end{equation}本記事では一貫して(4)ですので(13)は\begin{equation}\wp\left(\frac{\o_1}{2}-z\right)=\frac{1}{2}+\frac{5}{16\wp(z)-8}\tag{14}\end{equation}したがって(5)に対して\begin{equation}\wp\left(I\right)=\frac{1}{2}+\frac{5}{16a-8}\;,\;\wp\left(J\right)=\frac{1}{2}+\frac{5}{16b-8}\tag{15}\end{equation}(15)でペー関数の逆関数をとることにより\begin{equation}I=\int_{\frac{1}{2}+\frac{5}{16a-8}}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\;,\quad J=\int_{\frac{1}{2}+\frac{5}{16a-8}}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}\tag{16}\end{equation}
なお逆関数をとるときには注意が必要です。ペー関数は周期性を持つ偶関数なので(15)の逆関数をとると一般には$$\pm I+m\o_1+n\o_2=\int_{\frac{1}{2}+\frac{5}{16a-8}}^{+\infty}\frac{dx}{\sqrt{4x^3-g_2x-g_3}}$$です。しかし今は右辺が実数なので虚数周期である $\o_2$ は現れないので $n=0$ です。また $e_1<a$ という前提なので右辺の積分値は明らかに $(0,\frac{\o_1}{2})$ の範囲内です。そして(9)より $0<I<J<\frac{\o_1}{2}$ です。よって(16)が正しい逆関数のとり方になります。
(5)(16)より\begin{align}\int_{1/2}^{a}\frac{dx}{\sqrt{4x^3-\frac{7}{4}x+\frac{3}{8}}}=\int_{\frac{1}{2}+\frac{5}{16a-8}}^{\infty}\frac{dx}{\sqrt{4x^3-\frac{7}{4}x+\frac{3}{8}}}\end{align}が成り立ちます。あるいは $x\to x/4$ に戻して\begin{equation}\int_2^{4a}\cfrac{dx}{\sqrt{x^3-7x+6}}=\int_{2+\frac{5}{4a-2}}^{\infty}\cfrac{dx}{\sqrt{x^3-7x+6}}\tag{16.5}\end{equation}$a$ に値を代入していろいろな公式を得ますが、この式についての話はここまで。
ここで導出した2倍公式は\begin{equation}\wp(2z)=\frac{1}{4}\left(\frac{\wp''(z)}{\wp'(z)}\right)^2-2\wp(z)\tag{17}\end{equation}これと $\wp^{\prime 2}=4\wp^3-g_2\wp-g_3$ および $\wp''=6\wp^2-\frac{g_2}{2}$ から\begin{equation}\wp(2z)=\frac{1}{4}\frac{(6\wp(z)^2-\frac{g_2}{2})^2}{4\wp(z)^3-g_2\wp(x)-g_3}-2\wp(z)\tag{18}\end{equation}本記事のなかでは\begin{equation}\wp(2z)=\frac{1}{4}\frac{(6\wp(z)^2-\frac{7}{8})^2}{4\wp(z)^3-\frac{7}{4}\wp(z)+\frac{3}{8}}-2\wp(z)\tag{19}\end{equation}特に(15)より\begin{equation}\wp(2I)=\frac{256a^4+224a^2-192a+49}{32(2a-1)(4a-1)(4a+3)}\tag{20}\end{equation}
準備はここまで。最後に $\wp(J)=\wp(2I)$ となるような $a,b$ を見つけます。いくらでもありますが、いくつかの例を示します。
$a=3/4$ , $b=17/4$ とすると $\wp(I)=\frac{7}{4}$ であり$$\wp(J)=\wp(2I)=\frac{7}{12}$$よって $J=2I$ なので(1)より\begin{equation}\cfrac{\displaystyle\int_2^{17}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_2^{3}\cfrac{dx}{\sqrt{x^3-7x+6}}}=2\tag{21}\end{equation}
$a=1$ , $b=421/2$ とすると $\wp(I)=\frac{9}{8}$ であり$$\wp(J)=\wp(2I)=\frac{337}{672}$$よって $J=2I$ なので(1)より\begin{equation}\cfrac{\displaystyle\int_2^{842}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_2^{4}\cfrac{dx}{\sqrt{x^3-7x+6}}}=2\tag{22}\end{equation}
しかし $\wp(J)=\wp(2I)$ ならば $J=2I$ というのは必ずしも正しくありません。(21)(22)は正しいのですが、一般にそうではないのです。本当は$$2I=\pm J+m\o_1+n\o_2$$です。しかし $J,I$ は実数なので虚数周期 $\o_2$ は現れませんので$$2I=\pm J +m\o_1$$となります。$0<J<\frac{\o_1}{2}$ であることに注意して符号と $m$ を定めます。(21)(22)のときは $I$ちょうど正符号かつ $m=0$ だったのです。なお $\o_1/2 \approx 2.01891$ です。
$a=5/4$ , $b=61/2$ とすると $\wp(I)=\frac{11}{12}$ であり$$\wp(J)=\wp(2I)=\frac{49}{96}$$数値計算により $I\approx 1.1$ より $\frac{\o_1}{2}<I<\o_1$. よって $2I=-J+\o_1$ となる。なので(8)も用いて\begin{equation}\cfrac{\displaystyle\int_2^{122}\cfrac{dx}{\sqrt{x^3-7x+6}}}{\displaystyle\int_5^{\infty}\cfrac{dx}{\sqrt{x^3-7x+6}}}=2\tag{23}\end{equation}
冒頭で挙げた他の式については同様に導出できるので省略します。
楕円曲線との関連についても学びたいところです。
こちらに同様の例題があります:
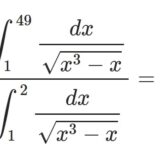 ペー関数を使って楕円積分を変換する具体例2
ペー関数を使って楕円積分を変換する具体例2
冒頭の第1式はこの本に載っていました。結果だけですが。

Auxiliary Polynomials in Number Theory
楽天はこちら
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。