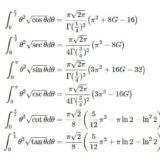We consider the integrals that have the product of $\arcsin x$ or $\arccos x$ and $x^s$ besides $\ln x$. The point is that $n$-times differentiation of $x^s$ w.r.t $s$ generates $\ln^nx$.
本日のお題はこちらです。
$s>-1$ における $\arcsin$ , $\arccos$ に関する積分公式\begin{eqnarray}\int_0^1 x^s\arcsin xdx&=&\frac{\pi}{2(s+1)}-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)\G(\frac{s+3}{2})}\\\int_0^1 x^s\ln x\arcsin xdx&=&-\frac{\pi}{2(s+1)^2}+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\\&&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{4(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\\\int_0^1 x^s\ln^2 x\arcsin xdx&=&\frac{\pi}{(s+1)^3}-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{(s+1)^3\G(\frac{s+3}{2})}\\&&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\\ && -\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]^2\\ &&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi'\left(\frac{s+3}{2}\right)-\psi'\left(\frac{s}{2}+1\right)\right]\end{eqnarray}\begin{eqnarray}\int_0^1 x^s\arccos xdx&=&\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)\G(\frac{s+3}{2})}\\\int_0^1 x^s\ln x\arccos xdx&=&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\\&&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{4(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\\\int_0^1 x^s\ln^2 x\arccos xdx&=&\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{(s+1)^3\G(\frac{s+3}{2})}\\&&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\\&&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]^2\\&&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi'\left(\frac{s+3}{2}\right)-\psi'\left(\frac{s}{2}+1\right)\right]\end{eqnarray}を導出する。これらに値を代入することにより、例えば次の等式を得る。\begin{eqnarray}\int_0^1\arcsin xdx &=& \frac{\pi}{2}-1\\ \int_0^1 x\arcsin xdx &=& \frac{\pi}{8}\\ \int_0^1 x^2\arcsin xdx &=& \frac{\pi}{6}-\frac{2}{9}\\ \int_0^1 \sqrt{x} \arcsin xdx &=&\frac{\pi}{3}-\frac{\G(\frac{1}{4})^2}{9\sqrt{2\pi}}\end{eqnarray}\begin{eqnarray}\int_0^1\ln x\arcsin xdx &=& 2-\frac{\pi}{2}-\ln2\\ \int_0^1 x\ln x\arcsin xdx &=& \frac{\pi}{8}(\ln2 -1)\\ \int_0^1 x^2\ln x\arcsin xdx &=& \frac{7}{27}-\frac{\pi}{18}-\frac{2}{9}\ln2\end{eqnarray}\begin{eqnarray}\int_0^1\ln^2 x\arcsin xdx &=& \frac{\pi^2}{12}+\pi-6+4\ln2-\ln^22\\ \int_0^1 x\ln^2 x\arcsin xdx &=& -\frac{\pi^3}{96}+\frac{3}{16}\pi-\frac{\pi}{8}\ln^22\\ \int_0^1 x^2\ln^2 x\arcsin xdx &=& \frac{\pi^2}{54}+\frac{\pi}{27}+\frac{14}{27}(\ln2-1)-\frac{2}{9}\ln^22\end{eqnarray}
上の式は非常にややこしく見えます。$x$ の累乗に $\arcsin$ さらには $\ln$ が混じっているからです。余程すごい置換などのトリックを使うのでしょうか?
しかし実は、高等なテクニックや閃きが生まれなくても、混じった $\ln$ を機械的に扱う手法があり、計算は泥臭くなりますが、無難に進めることができます。
本稿の軸となる積分を次で定義します。
\begin{equation}I(s):=\int_0^1 x^s\arcsin xdx\quad(s>-1)\tag{1}\end{equation}
$\log$ を登場させる常套手段として、これを $s$ で微分します。$$\frac{dI}{ds}=\int_0^1 x^s\ln x\arcsin xdx$$繰り返し微分することで次を得ます。
\begin{equation}\frac{d^nI}{ds^n}=\int_0^1 x^s\ln^nx\arcsin xdx\tag{2}\end{equation}
$I(s)$ を $s$ の関数として表すことができれば、任意の回数微分して、好きに $s$ を代入することで冒頭のような積分たちを導くことができます。本日の肝はこれで終わりといっていいくらいです。
では $I(s)$ を求めましょう。(1)で部分積分すると$$I(s)=\frac{\pi}{2(s+1)}-\frac{1}{s+1}\int_0^1\frac{x^{s+1}}{\sqrt{1-x^2}}dx$$ここで次の級数展開を利用します。$$\frac{1}{\sqrt{1-X}}=\sum_{n=0}^\infty\frac{(2n-1)!!}{n!2^n}X^n$$すなわち$$I(s)=\frac{\pi}{2(s+1)}-\frac{1}{s+1}\sum_{n=0}^\infty\frac{(2n-1)!!}{n!2^n}\int_0^1 x^{2n+s+1}dx$$積分を実行します。$$I(s)=\frac{\pi}{2(s+1)}-\frac{1}{s+1}\sum_{n=0}^\infty\frac{(2n-1)!!}{n!2^n(2n+s+2)}$$シグマの中身をポッホハマー記号で書き改めると$$I(s)=\frac{\pi}{2(s+1)}-\frac{1}{(s+1)(s+2)}\sum_{n=0}^\infty\frac{(\frac{s}{2}+1)_n(\frac{1}{2})_n}{n!(\frac{s}{2}+2)_n}$$この総和はガウスの超幾何級数ですので$$I(s)=\frac{\pi}{2(s+1)}-\frac{1}{(s+1)(s+2)}F\left(\frac{s}{2}+1,\frac{1}{2},\frac{s}{2}+2;1\right)$$ガウスの超幾何定理を用いると$$I(s)=\frac{\pi}{2(s+1)}-\frac{1}{(s+1)(s+2)}\frac{\sqrt{\pi}\G(\frac{s}{2}+2)}{\G(\frac{s+3}{2})}$$分子のガンマ関数を少しいじれば以下の等式が導かれます。
\begin{eqnarray}I(s)&:=&\int_0^1 x^s\arcsin xdx\\&=&\frac{\pi}{2(s+1)}-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)\G(\frac{s+3}{2})}\tag{3}\end{eqnarray}
あとはこれを好きな回数微分して $s$ に値を入れれば、多くの積分値が得られます。ガンマ関数の中身を見れば、$s$ が非負整数であれば初等的な形で表すことができると分かります。たとえば $s=0,\:1,\:2$ あるいは $1/2$ とすれば
\begin{eqnarray}\int_0^1\arcsin xdx &=& \frac{\pi}{2}-1\tag{4}\\ \int_0^1 x\arcsin xdx &=& \frac{\pi}{8}\tag{5}\\ \int_0^1 x^2\arcsin xdx &=& \frac{\pi}{6}-\frac{2}{9}\tag{6}\\ \int_0^1 \sqrt{x} \arcsin xdx &=&\frac{\pi}{3}-\frac{\G(\frac{1}{4})^2}{9\sqrt{2\pi}}\tag{7}\end{eqnarray}
$I(s)$ を微分すると(2)より
\begin{eqnarray}\frac{dI}{ds}&=&\int_0^1 x^s\ln x\arcsin xdx\\&=&-\frac{\pi}{2(s+1)^2}+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\\&&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{4(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\tag{8}\end{eqnarray}
ここで $\psi(x)$ はディガンマ関数です。以下ではディガンマ関数の基本的な式$$\psi(z+1)=\psi(z)+\frac{1}{z}$$$$\psi(1)=-\g\quad,\quad\psi\left(\frac{1}{2}\right)=-\g-2\ln2$$を押さえておきましょう。詳しくは過去記事
を参照ください。
(8)で $s=0,1,2$ としてみると
\begin{eqnarray}\int_0^1\ln x\arcsin xdx &=& 2-\frac{\pi}{2}-\ln2\tag{9}\\ \int_0^1 x\ln x\arcsin xdx &=& \frac{\pi}{8}(\ln2 -1)\tag{10}\\ \int_0^1 x^2\ln x\arcsin xdx &=& \frac{7}{27}-\frac{\pi}{18}-\frac{2}{9}\ln2\tag{11}\end{eqnarray}
意外にシンプルな値になりました。$s$ が整数のときは初等的な計算方法があるのではないかと考えたくなりますね。
この調子でさらに(8)を微分して $\log x$ の次数が増えます。大変そうですが、ミスなきように気を付けます。
\begin{eqnarray}\frac{d^2I}{ds^2}&=&\int_0^1 x^s\ln^2 x\arcsin xdx\\&=&\frac{\pi}{(s+1)^3}-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{(s+1)^3\G(\frac{s+3}{2})}\\&&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\\ && -\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]^2\\ &&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi'\left(\frac{s+3}{2}\right)-\psi'\left(\frac{s}{2}+1\right)\right]\tag{12}\end{eqnarray}
共通する因子もありますので、適宜くくってもいいでしょう。$s=0,1,2$ としてみると
\begin{eqnarray}\int_0^1\ln^2 x\arcsin xdx &=& \frac{\pi^2}{12}+\pi-6+4\ln2-\ln^22\tag{13}\\ \int_0^1 x\ln^2 x\arcsin xdx &=& -\frac{\pi^3}{96}+\frac{3}{16}\pi-\frac{\pi}{8}\ln^22\tag{14}\\ \int_0^1 x^2\ln^2 x\arcsin xdx &=& \frac{\pi^2}{54}+\frac{\pi}{27}+\frac{14}{27}(\ln2-1)-\frac{2}{9}\ln^22\tag{15}\end{eqnarray}
$\arccos$ でも同様に$$J(s):=\int_0^1x^s\arccos xdx$$$\arcsin x+\arccos x=\frac{\pi}{2}$ なので$$J(s)=\frac{\pi}{2(s+1)}-I(s)$$よって
\begin{eqnarray}J(s)&:=&\int_0^1 x^s\arccos xdx\\&=&\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)\G(\frac{s+3}{2})}\tag{16}\end{eqnarray}
$I(s)$ よりも若干シンプルな式になりました。先にこっちからやればよかったですね。あとは同様に計算するだけです。
1度目の微分により
\begin{eqnarray}\int_0^1 x^s\ln x\arccos xdx&=&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\\&&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{4(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\tag{17}\end{eqnarray}
再度微分します。
\begin{eqnarray}\int_0^1 x^s\ln^2 x\arccos xdx&=&\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{(s+1)^3\G(\frac{s+3}{2})}\\&&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{2(s+1)^2\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]\\&&+\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi\left(\frac{s+3}{2}\right)-\psi\left(\frac{s}{2}+1\right)\right]^2\\&&-\frac{\sqrt{\pi}\G(\frac{s}{2}+1)}{8(s+1)\G(\frac{s+3}{2})}\left[\psi'\left(\frac{s+3}{2}\right)-\psi'\left(\frac{s}{2}+1\right)\right]\tag{18}\end{eqnarray}
(16)(17)(18)の $s$ に値を代入すればいろいろな公式を得られます。例えば$$\int_0^1x\ln x\arccos xdx=-\frac{\pi\ln2}{8}$$$$\int_0^1x\ln^2 x\arccos xdx=\frac{\pi^3}{96}+\frac{\pi\ln^22}{8}-\frac{\pi}{16}$$の感じです。
こちらもどうぞ:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。