複素積分によって求めたフレネル積分を一般化して考えることによって、求める積分値はガンマ関数を用いて表現できることが分かる。複素積分で使う経路は扇形である。またこの積分はエアリー関数の特殊な場合としても現れることを補足する。
前の記事では $\displaystyle\int^\infty_0\cos (x^2)dx$ と $\displaystyle\int^\infty_0\sin (x^2)dx$ の値を計算しました。
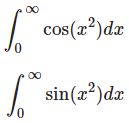【複素解析】フレネル積分-三角関数の特殊な積分 sin x^2 , cos x^2
中心角 $\pi/4$ の扇形に沿った複素積分をすることでうまく求まりましたので、これを応用して今回はサイン・コサインの引数が3乗の定積分を検討します。
２つの定積分$$I=\int^\infty_0\cos (x^3)dx$$$$J=\int^\infty_0\sin (x^3)dx$$はいかなる値か．
先に結論を述べておきますと、これらは初等的には解けず、ガンマ関数を使って$$\begin{cases}\displaystyle\int^\infty_0\cos (x^3)dx=\displaystyle\frac{\Gamma(1/3)}{2\sqrt{3}}\\[2em]\displaystyle\int^\infty_0\sin (x^3)dx=\displaystyle\frac{\Gamma(1/3)}{6}\end{cases}$$となります。これの導出方法は上述の記事とほぼ同じですが、今度は下図のように中心角 $\pi/6$ で半径 $R$ の扇形を積分経路として$$\oint_C e^{iz^3}dz$$を考えます。
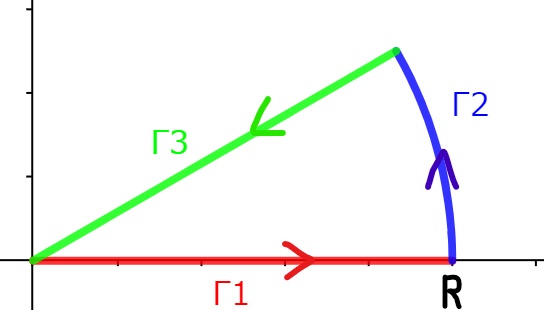
被積分関数は閉曲線内で極をもたないため、コーシーの積分定理より周回積分は $0$ となります。扇形を $\Gamma_1$ , $\Gamma_2$ , $\Gamma_3$ の3つに分割して考えると$$0=\oint_Ce^{iz^3}dz=\int^R_0e^{ix^3}dx+\int_{\Gamma_2}e^{iz^3}dz+\int_{\Gamma_3}e^{iz^3}dz$$右辺第1項は $\Gamma_1$ に関する積分のことです。この項について $R\to\infty$ の極限を考えると冒頭の $I,J$ が求まるわけです。以下、問題形式で進めていきます。
$\Gamma_2$ の線積分において $z=Re^{i\theta}$ と置換し，$R\to\infty$ としたときの積分値を計算せよ．
置換してみると $e$ の $e$ 乗が出てくるので三角関数に直してやります。\begin{eqnarray*}\int_{\Gamma_2}e^{iz^3}dz &=& i\int^{\frac{\pi}{6}}_0Re^{i\theta}e^{iR^3(\cos3\theta+i\sin3\theta)}d\theta\\&=& i\int^{\frac{\pi}{6}}_0Re^{i\theta}e^{R^3(i\cos3\theta-\sin3\theta)}d\theta\end{eqnarray*}この結果の絶対値をとって評価すると\begin{eqnarray*}\left| i\int^{\frac{\pi}{6}}_0Re^{i\theta}e^{R^3(i\cos3\theta-\sin3\theta)}d\theta \right| &=& \left| \int^{\frac{\pi}{6}}_0Re^{i\theta}e^{iR^3\cos3\theta}e^{-R^3\sin3\theta}d\theta \right|\\ &\leq & \int^{\frac{\pi}{6}}_0R\left| e^{i\theta}e^{iR^3\cos3\theta}e^{-R^3\sin3\theta}\right| d\theta\\ &=& \int^{\frac{\pi}{6}}_0R\left| e^{-R^3\sin3\theta}\right| d\theta\xrightarrow[R\to\infty]{}0\end{eqnarray*}よって求める積分値は$0$となります。
$\Gamma_3$ の線積分において $z=e^{i\frac{\pi}{6}}x$ と置換し，$R\to\infty$ としたときの積分値を計算せよ．
$\Gamma_3$ は点 $Re^{i\frac{\pi}{6}}$ から点 $0$ を結ぶ線分なので $x$ の範囲は $[0,R]$ となります（向きは$R$から$0$）。$z^3=e^{i\frac{\pi}{2}}x^3=ix^3$ より\begin{eqnarray*}\int_{\Gamma_3}e^{iz^3}dz &=& \int^0_Re^{-x^3}\cdot e^{\frac{\pi}{6}i}dx\\ &\xrightarrow[R\to\infty]{}& -e^{\frac{\pi}{6}i}\int^\infty_0e^{-x^3}dx\\ &=& -e^{\frac{\pi}{6}i}\cdot \frac{1}{3}\Gamma\left(\frac{1}{3}\right)\end{eqnarray*}最後の等号は $x^3=t$ とおいて\begin{eqnarray*}\int^\infty_0e^{-x^3}dx&=&\int^\infty_0e^{-t}\cdot \frac{1}{3}t^{\frac{1}{3}-1}dt\\ &=& \frac{1}{3}\Gamma\left(\frac{1}{3}\right)\end{eqnarray*}としたものです。ここでガンマ関数の定義は $\Gamma(x)=\displaystyle\int^\infty_0e^{-t}t^{x-1}dt$ です。
これで $\Gamma_3$ の積分が終わりました。
以上の結果から，冒頭の $I$ および $J$ を求めよ．
周回積分の３分割を再度示すと$$0=\oint_Ce^{iz^3}dz=\int^R_0e^{ix^3}dx+\int_{\Gamma_2}e^{iz^3}dz+\int_{\Gamma_3}e^{iz^3}dz$$$R\to\infty$ として $\Gamma_2$ と $\Gamma_3$ の積分値を代入すると$$0=\int^\infty_0e^{ix^3}dx+0-e^{\frac{\pi}{6}i}\cdot \frac{1}{3}\Gamma\left(\frac{1}{3}\right)$$すなわち$$\int^\infty_0e^{ix^3}dx=e^{\frac{\pi}{6}i}\cdot \frac{1}{3}\Gamma\left(\frac{1}{3}\right)$$$$\therefore \int^\infty_0 e^{ix^3}dx=\frac{\Gamma(1/3)}{2\sqrt{3}}+\frac{\Gamma(1/3)}{6}i$$$e^{ix^3}=\cos(x^3)+i\sin(x^3)$ より、両辺の実部と虚部を比べると最終結果を得ます。
$$\begin{cases}\displaystyle\int^\infty_0\cos (x^3)dx=\displaystyle\frac{\Gamma(1/3)}{2\sqrt{3}}\\[2em]\displaystyle\int^\infty_0\sin (x^3)dx=\displaystyle\frac{\Gamma(1/3)}{6}\end{cases}$$
エアリー方程式$$y^{\prime\prime}-xy=0$$の特殊解として第1種エアリー函数$$\textrm{Ai}(x)=\frac{1}{\pi}\int^\infty_0\cos\left(\frac{t^3}{3}+xt \right)dt$$という特殊函数があります。今回求めた積分は$\textrm{Ai}(0)$としてあらわれます。
前回は2乗、今回は3乗の積分を行いました。前者の場合はガンマ関数の値が明示できたのでよかったですが、今回は $\Gamma(1/3)$ が現れて先へは進めません。でもとにかく解法は同じです。
扇形の中心角を $\dfrac{\pi}{4}$ , $\dfrac{\pi}{6}$ としたのは、それぞれ $e^{-x^2}$ , $e^{-x^3}$ を生みだすことでガンマ関数に帰着させられるためです（ガンマ関数を答えに残してしまうので「解けた」とは言えないのでしょうが、ガンマ関数はよく知られた関数で、すっきり表現できます）。
なので、まったく同様の手法で$n$乗でもできそうです。その場合は扇形の中心角を $\dfrac{\pi}{2n}$ とすればよいことが予想できます。
⇒やってみました
【複素解析】cos(x^n),sin(x^n) の定積分（フレネル積分を一般化）
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。