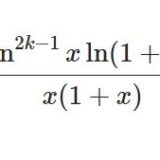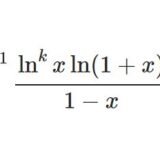前回の続きです。前回はこちら。
\begin{align}\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx&=(2k-1)!\left[\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)-\frac{2k+1}{2}\eta(2k+1)\right]\\\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx&=(2k-1)!\left[-\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)+\frac{2k-1}{2}\eta(2k+1)\right]\\\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx&=\frac{(-1)^{k-1}}{2}(k+1)!\zeta(k+2)+\frac{(-1)^k}{2}k!\sum_{r=2}^{k}\zeta(r)\zeta(k-r+2)\\\int_0^1\frac{\ln^kx\ln(1-x)}{x(1-x)}dx&=\frac{(-1)^{k-1}(k+3)}{2}k!\zeta(k+2)+\frac{(-1)^k}{2}k!\sum_{r=2}^{k}\zeta(r)\zeta(k-r+2)\\\sum_{n=1}^\infty\frac{(-1)^{n-1}H_n}{n^{2q}}&=\frac{2q+1}{2}\eta(2q+1)-\sum_{l=0}^{q-1}\eta(2l)\zeta(2q-2l+1)\\\sum_{n=1}^\infty\frac{H_n}{n^q}&=\frac{q+2}{2}\zeta(q+1)-\frac{1}{2}\sum_{r=2}^{q-1}\zeta(r)\zeta(q-r+1)\end{align}
前回の(15)式で\begin{equation}\int_0^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx=2\cdot(2k-1)!\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)\tag{1}\end{equation}を導出しました。これに留意して$$I:=\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx$$の計算をします(実は過去記事で $k=2$ の場合を導出済み)。まず$$I=\int_0^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx-\int_1^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx$$右辺2つめの積分では $x\to\frac{1}{x}$ と置換します。\begin{equation}I=\int_0^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx+\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx-\int_0^1\frac{\ln^{2k}x}{1+x}dx\tag{2}\end{equation}一方で部分分数分解により$$I=\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{x}dx-\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx$$であり、右辺1つめの積分を部分積分すると$$I=-\frac{1}{2k}\int_0^1\frac{\ln^{2k}x}{1+x}dx-\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx$$(2)と辺々足すと\begin{equation}2I=\int_0^\infty\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx-\frac{2k+1}{2k}\int_0^1\frac{\ln^{2k}x}{1+x}dx\tag{3}\end{equation}(3)の右辺第1項はまさに(1)です。第2項は、これまた前回の記事で現れた$$\int_0^1\frac{\ln^kx}{1+x}dx=(-1)^kk!\:\eta(k+1)$$を使えばよいです。式を整理すると$$I=(2k-1)!\left[\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)-\frac{2k+1}{2}\eta(2k+1)\right]$$以上から次の2式を得ます。
\begin{align}\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{x(1+x)}dx&=(2k-1)!\left[\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)-\frac{2k+1}{2}\eta(2k+1)\right]\tag{a}\\\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx&=(2k-1)!\left[-\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)+\frac{2k-1}{2}\eta(2k+1)\right]\tag{b}\end{align}
定理5からある奇数weightのEuler-sumが求まります。過去にはEuler-sumに関する記事を多く書いていますが、また新しい知見です。といっても手法としてはこちらの過去記事でも紹介しているのですが…。
まず部分積分を繰り返すことで得られる式\begin{equation}\int_0^1x^{n-1}\ln^{q-1}xdx=(q-1)!\frac{(-1)^{q-1}}{n^q}\tag{4}\end{equation}に $(-1)^{n-1}H_n$ をかけて $n$ について和をとります。\begin{equation}\int_0^1\sum_{n=1}^\infty\left(H_n(-x)^{n-1}\right)\ln^{q-1}xdx=(-1)^{q-1}(q-1)!\sum_{n=1}^\infty\frac{(-1)^{n-1}H_n}{n^q}\tag{5}\end{equation}ここで、こちらで求めた調和数を生成する母関数\begin{equation}\sum_{n=1}^\infty H_nx^n=-\frac{\ln(1-x)}{1-x}\tag{6}\end{equation}の $x$ を $-x$ として(5)に用います。\begin{equation}\int_0^1\frac{\ln^{q-1}x\ln(1+x)}{x(1+x)}dx=(-1)^{q-1}(q-1)!\sum_{n=1}^\infty\frac{(-1)^{n-1}H_n}{n^q}\tag{7}\end{equation}$q$ が偶数のときにまさに定理5(a)が使えます。よって
$$\sum_{n=1}^\infty\frac{(-1)^{n-1}H_n}{n^{2q}}=-\sum_{l=0}^{q-1}\eta(2l)\zeta(2q-2l+1)+\frac{2q+1}{2}\eta(2q+1)$$
$\int \frac{\ln^{k-1}x\ln(1-x)}{x(1-x)}dx$ が分かれば、同様の手法で $\sum\frac{H_n}{n^q}$ を計算できます。あとでやりましょう。
前回記事と似た方法を使います。$k\in\NN$ に対し$$\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx=\lim_{s\to1}\lim_{t\to0}\frac{\partial^k}{\partial s^k}\frac{\partial}{\partial t}\int_0^1x^{s-1}(1-x)^{t-1}dx$$ベータ関数の積分表示から$$\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx=\lim_{s\to1}\lim_{t\to0}\frac{\partial^k}{\partial s^k}\frac{\partial}{\partial t}\frac{\G(s)\G(t)}{\G(s+t)}$$$t$ での微分を実行すると\begin{equation}\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx=\lim_{s\to1}\lim_{t\to0}\frac{\partial^k}{\partial s^k}\frac{\G(s)\G(t)}{\G(s+t)}\left[\psi(t)-\psi(s+t)\right]\tag{8}\end{equation}この段階では $t\to0$ では発散してしまいます。先に $s$ での微分を実行する必要があります(ベータ関数 $B(s,t)$ の偏導関数は、ベータ関数そのものよりも $s,t$ の定義域が広い)。すると\begin{align}&=\lim_{s\to1}\lim_{t\to0}\frac{\partial^{k-1}}{\partial s^{k-1}}\frac{\G(s)\G(t)}{\G(s+t)}\left[\left(\psi(s)-\psi(s+t)\right)\left(\psi(t)-\psi(s+t)\right)-\psi'(s+t)\right]\\&=\lim_{s\to1}\lim_{t\to0}\frac{\partial^{k-1}}{\partial s^{k-1}}\frac{\G(s)\G(t+1)}{\G(s+t)}\left[\frac{\psi(s)-\psi(s+t)}{t}\left(\psi(t+1)-\frac{1}{t}-\psi(s+t)\right)-\frac{\psi'(s+t)}{t}\right]\\&=\lim_{s\to1}\lim_{t\to0}\frac{\partial^{k-1}}{\partial s^{k-1}}\frac{\G(s)\G(t+1)}{\G(s+t)}\left[\frac{\psi(s)-\psi(s+t)}{t}\left(\psi(t+1)-\psi(s+t)\right)-\frac{\psi(s)-\psi(s+t)+t\psi'(s+t)}{t^2}\right]\end{align}式が煩雑になるのを避けるため、一部 $t\to0$ を実行します。\begin{align}&=\lim_{s\to1}\lim_{t\to0}\frac{\partial^{k-1}}{\partial s^{k-1}}\left[-\psi'(s)\left(\psi(1)-\psi(s)\right)-\frac{\psi(s)-\psi(s+t)+t\psi'(s+t)}{t^2}\right]\\&=\lim_{s\to1}\lim_{t\to0}\frac{\partial^{k-1}}{\partial s^{k-1}}\left[\psi'(s)\left(\psi(s)+\g\right)-\frac{\psi(s)-\psi(s+t)+t\psi'(s+t)}{t^2}\right]\end{align}分数のところは $t\to0$ についてロピタルの定理により$$=\lim_{s\to1}\lim_{t\to0}\frac{\partial^{k-1}}{\partial s^{k-1}}\left[\psi'(s)\left(\psi(s)+\g\right)-\frac{\psi''(s+t)}{2}\right]$$よって\begin{equation}\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx=\lim_{s\to1}\frac{d^{k-1}}{ds^{k-1}}\left[\psi'(s)\left(\psi(s)+\g\right)-\frac{\psi''(s)}{2}\right]\tag{9}\end{equation}(9)右辺の微分を実行します。 $\psi'\psi$ についてはライプニッツルールを使って$$=\lim_{s\to1}\left[-\frac{1}{2}\psi^{(k+1)}(s)+\g\psi^{(k)}(s)+\sum_{r=0}^{k-1}\binom{k-1}{r}\psi^{(r)}(s)\psi^{(k-r)}(s)\right]$$ここでポリガンマ関数に関するこちらの記事より\begin{equation}\psi^{(n)}(1)=(-1)^{n+1}n!\zeta(n+1)\tag{10}\end{equation}に注意して $s\to1$ を実行します。ただし総和の $r=0$ だけ特別で、$\psi(1)=-\g$ です。\begin{align}&=-\frac{1}{2}\psi^{(k+1)}(1)+\g\psi^{(k)}(1)-\g\psi^{(k)}(1)+\sum_{r=1}^{k-1}\binom{k-1}{r}\psi^{(r)}(1)\psi^{(k-r)}(1)\\&=\frac{1}{2}\psi^{(k+1)}(1)\sum_{r=1}^{k-1}\binom{k-1}{r}\psi^{(r)}(1)\psi^{(k-r)}(1)\\&=\frac{(-1)^{k-1}}{2}(k+1)!\zeta(k+2)+(-1)^k(k-1)!\sum_{r=1}^{k-1}(k-r)\zeta(r+1)\zeta(k-r+1)\end{align}残った総和は、逆に並べて足すことで\begin{equation}2\times\sum_{r=1}^{k-1}(k-r)\zeta(r+1)\zeta(k-r+1)=k\sum_{r=2}^{k}\zeta(r)\zeta(k-r+2)\tag{11}\end{equation}と分かりますから
$$\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx=\frac{(-1)^{k-1}}{2}(k+1)!\zeta(k+2)+\frac{(-1)^k}{2}k!\sum_{r=2}^{k}\zeta(r)\zeta(k-r+2)$$$$\int_0^1\frac{\ln^kx\ln(1-x)}{x(1-x)}dx=\frac{(-1)^{k-1}(k+3)}{2}k!\zeta(k+2)+\frac{(-1)^k}{2}k!\sum_{r=2}^{k}\zeta(r)\zeta(k-r+2)$$
なお定理7の2行目については、部分分数分解と前回の記事の定理3(10)を用いることですぐに導出できます。
系6と同様のことをやってみましょう。(4)に $H_n$ をかけて和をとります。\begin{equation}\int_0^1\sum_{n=1}^\infty\left(H_nx^{n-1}\right)\ln^{q-1}xdx=(-1)^{q-1}(q-1)!\sum_{n=1}^\infty\frac{H_n}{n^q}\tag{12}\end{equation}(6)より\begin{equation}\int_0^1\frac{\ln^{q-1}x\ln(1-x)}{x(1-x)}dx=(-1)^{q}(q-1)!\sum_{n=1}^\infty\frac{H_n}{n^q}\tag{13}\end{equation}定理7により
$$\sum_{n=1}^\infty\frac{H_n}{n^q}=\frac{q+2}{2}\zeta(q+1)-\frac{1}{2}\sum_{r=2}^{q-1}\zeta(r)\zeta(q-r+1)$$
今日はここまで。
次回:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。