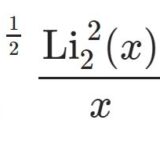前回はこちら:
\begin{align}\int_0^1\frac{\ln^kx\ln(1-x)}{\sqrt{x}(1-x)}dx &=\frac{(-1)^{k+1}}{2}(k+1)!(2^{k+2}-1)\zeta(k+2)\\&\quad+2(-1)^kk!(2^{k+1}-1)\zeta(k+1)\ln2\\&\quad+\frac{(-1)^k}{2}k!\sum_{r=2}^k(2^r-1)(2^{k-r+2}-1)\zeta(r)\zeta(k-r+2)\\\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx&=(-1)^{k+1}(k+1)!\left(1-\frac{1}{2^{k+2}}\right)\zeta(k+2)\\&\quad+2(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\ln2\\&\quad+(-1)^kk!\sum_{r=2}^k\left(1-\frac{1}{2^r}\right)\left(1-\frac{1}{2^{k-r+2}}\right)\zeta(r)\zeta(k-r+2)\\\int_0^1\frac{\ln^kx\ln(1+x)}{1-x}dx&=\frac{(-1)^{k+1}}{2}(k+1)!\zeta(k+2)\\&\quad+2(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\ln2\\&\quad+\frac{(-1)^k}{2}k!\sum_{r=2}^k\left(1-\frac{1}{2^{r-1}}\right)\left(1-\frac{1}{2^{k-r+1}}\right)\zeta(r)\zeta(k-r+2)\end{align}
\begin{align}\sum_{n=0}^\infty\frac{H_n}{(2n+1)^k}&=k\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\\&\quad-2\left(1-\frac{1}{2^{k}}\right)\zeta(k)\ln2\\&\quad-\sum_{r=2}^{k-1}\left(1-\frac{1}{2^r}\right)\left(1-\frac{1}{2^{k-r+1}}\right)\zeta(r)\zeta(k-r+1)\\\sum_{n=0}^\infty\frac{h_n}{n^k}&=k\left(1-\frac{1}{2^k}-\frac{k}{2}\right)\zeta(k+1)\\&\quad+2\left(1-\frac{1}{2^{k}}\right)\zeta(k)\ln2\\&\quad+\frac{1}{2}\sum_{r=2}^{k-1}\eta(r)\eta(k-r+1)\end{align}
$x^2=y$ なる置換により\begin{equation}\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx=\frac{1}{2^{k+1}}\int_0^1\frac{\ln^ky\ln(1-y)}{\sqrt{y}(1-y)}dy\tag{1}\end{equation}右辺の積分を計算します。前回と同様にベータ関数の微分を用いてやります。つまり$$\int_0^1\frac{\ln^kx\ln(1-x)}{\sqrt{x}(1-x)}dx=\lim_{s\to1/2}\lim_{t\to0}\frac{\partial^k}{\partial s^k}\frac{\partial}{\partial t}\int_0^1x^{s-1}(1-x)^{t-1}dx$$前回と違うのは $s\to1/2$ の部分だけで、ほかは全く同じです。なので前回の計算の途中$$=\lim_{s\to1/2}\left[-\frac{1}{2}\psi^{(k+1)}(s)+\g\psi^{(k)}(s)+\sum_{r=0}^{k-1}\binom{k-1}{r}\psi^{(r)}(s)\psi^{(k-r)}(s)\right]$$までは良しとしましょう。よって$$=-\frac{1}{2}\psi^{(k+1)}\left(\frac{1}{2}\right)+\g\psi^{(k)}\left(\frac{1}{2}\right)+\sum_{r=0}^{k-1}\binom{k-1}{r}\psi^{(r)}\left(\frac{1}{2}\right)\psi^{(k-r)}\left(\frac{1}{2}\right)$$ディガンマ関数の公式 $\psi(1/2)=-\g-2\ln2$ とポリガンマ関数に関するこちらの記事より\begin{equation}\psi^{(n)}\left(\frac{1}{2}\right)=(-1)^{n+1}n!(2^{n+1}-1)\zeta(n+1)\quad(n\in\NN)\tag{2}\end{equation}なので、総和の $r=0$ のみ別で計算することに注意して\begin{align}\int_0^1\frac{\ln^kx\ln(1-x)}{\sqrt{x}(1-x)}dx &=\frac{(-1)^{k+1}}{2}(k+1)!(2^{k+2}-1)\zeta(k+2)\\&\quad-2\ln2(-1)^{k+1}k!(2^{k+1}-1)\zeta(k+1)\\&\quad+(k-1)!(-1)^k\sum_{r=1}^{k-1}(k-r)(2^{r+1}-1)(2^{k-r+1}-1)\zeta(r+1)\zeta(k-r+1)\end{align}$k=1$ のときは右辺の和をとらないことにすればOK。ここで右辺の和を $S$ とします。$S$ を逆に並べてもとの $S$ と足し合わせると$$2S=k\sum_{r=1}^{k-1}(2^{r+1}-1)(2^{k-r+1}-1)\zeta(r+1)\zeta(k-r+1)$$以上によって次の結果を得ます。総和の添え字は1つずらしました。
\begin{align}\int_0^1\frac{\ln^kx\ln(1-x)}{\sqrt{x}(1-x)}dx &=\frac{(-1)^{k+1}}{2}(k+1)!(2^{k+2}-1)\zeta(k+2)\\&\quad+2(-1)^kk!(2^{k+1}-1)\zeta(k+1)\ln2\\&\quad+\frac{(-1)^k}{2}k!\sum_{r=2}^k(2^r-1)(2^{k-r+2}-1)\zeta(r)\zeta(k-r+2)\end{align}\begin{align}\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx&=(-1)^{k+1}(k+1)!\left(1-\frac{1}{2^{k+2}}\right)\zeta(k+2)\\&\quad+2(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\ln2\\&\quad+(-1)^kk!\sum_{r=2}^k\left(1-\frac{1}{2^r}\right)\left(1-\frac{1}{2^{k-r+2}}\right)\zeta(r)\zeta(k-r+2)\end{align}
定理9の2つめの式は(1)から求まりました。
前回は積分からEuler-sumを求める方法を紹介しましたが、今回も定理9を使って同様のことをやってみます。すなわち\begin{equation}\sum_{n=1}^\infty H_nx^n=-\frac{\ln(1-x)}{1-x}\tag{3}\end{equation}を用いてから繰り返し部分積分することにより\begin{align}\int_0^1\frac{\ln^kx\ln(1-x)}{\sqrt{x}(1-x)}dx&=-\sum_{n=1}^\infty H_n\int_0^1x^{n-\frac{1}{2}}\ln^kxdx\\&=k!(-1)^{k-1}\sum_{n=0}^\infty\frac{H_n}{(n+\frac{1}{2})^{k+1}}\\&=k!(-1)^{k-1}2^{k+1}\sum_{n=0}^\infty\frac{H_n}{(2n+1)^{k+1}}\end{align}よって(1)より\begin{equation}\sum_{n=0}^\infty\frac{H_n}{(2n+1)^{k+1}}=\frac{(-1)^{k-1}}{k!}\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx\tag{4}\end{equation}定理9より次の系が導出されます。なお $k$ を $k-1$ と改めました。
$k\in\ZZ_{\ge2}$,\begin{align}\sum_{n=0}^\infty\frac{H_n}{(2n+1)^k}&=k\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\\&\quad-2\left(1-\frac{1}{2^{k}}\right)\zeta(k)\ln2\\&\quad-\sum_{r=2}^{k-1}\left(1-\frac{1}{2^r}\right)\left(1-\frac{1}{2^{k-r+1}}\right)\zeta(r)\zeta(k-r+1)\end{align}
ただし $k=2$ では総和を無視します。
一見かなり難しい積分$$\int_0^1\frac{\ln^kx\ln(1+x)}{1-x}dx$$を紹介します。$(1+x)(1-x)=1-x^2$ より$$=\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x}dx-\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx$$右辺第1項に $\frac{1}{1-x}=\frac{1+x}{1-x^2}$ を使えば$$=\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx+\int_0^1\frac{x\ln^kx\ln(1-x^2)}{1-x^2}dx-\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx$$第2項で $x^2$ を $x$ に置換することで$$=\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx+\frac{1}{2^{k+1}}\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx-\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx$$よって\begin{equation}\int_0^1\frac{\ln^kx\ln(1+x)}{1-x}dx=\int_0^1\frac{\ln^kx\ln(1-x^2)}{1-x^2}dx+\left(\frac{1}{2^{k+1}}-1\right)\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx\tag{5}\end{equation}右辺の積分2つはそれぞれ定理9と前回記事の定理7:$$\int_0^1\frac{\ln^kx\ln(1-x)}{1-x}dx=\frac{(-1)^{k-1}}{2}(k+1)!\zeta(k+2)+\frac{(-1)^k}{2}k!\sum_{r=2}^{k}\zeta(r)\zeta(k-r+2)$$を用いれば完成です。
\begin{align}\int_0^1\frac{\ln^kx\ln(1+x)}{1-x}dx&=\frac{(-1)^{k+1}}{2}(k+1)!\zeta(k+2)\\&\quad+2(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\ln2\\&\quad+\frac{(-1)^k}{2}k!\sum_{r=2}^k\left(1-\frac{1}{2^{r-1}}\right)\left(1-\frac{1}{2^{k-r+1}}\right)\zeta(r)\zeta(k-r+2)\end{align}
$\eta$ を使うなら\begin{align}\int_0^1\frac{\ln^kx\ln(1+x)}{1-x}dx&=\frac{(-1)^{k+1}}{2}(k+1)!\zeta(k+2)\\&\quad+2(-1)^kk!\left(1-\frac{1}{2^{k+1}}\right)\zeta(k+1)\ln2\\&\quad+\frac{(-1)^k}{2}k!\sum_{r=2}^k\eta(r)\eta(k-r+2)\end{align}と書いてもよいです。
例えば\begin{equation}\int_0^1\frac{\ln^3x\ln(1+x)}{1-x}dx=12\zeta(5)-\frac{45}{4}\zeta(4)\ln2-\frac{9}{4}\zeta(2)\zeta(3)\tag{6}\end{equation}です。
さらに別の積分ですが、部分分数分解により$$\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1-x^2}dx=\frac{1}{2}\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx+\frac{1}{2}\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1-x}dx$$第2項は先ほどの定理11から、第1項は前回記事の定理5:$$\int_0^1\frac{\ln^{2k-1}x\ln(1+x)}{1+x}dx=(2k-1)!\left[\frac{2k-1}{2}\eta(2k+1)-\sum_{l=0}^{k-1}\eta(2l)\zeta(2k-2l+1)\right]$$が使えます。整理して終わりですが、あまりきれいな式にならないので結果は書かないでおきます。
また、$$\int_0^1\frac{\ln(1+x)\ln^{2k-1}\frac{1-x}{1+x}}{x}dx$$は $y=\frac{1-x}{1+x}$ と置換して$$\int_0^1\frac{\ln(1+x)\ln^{2k-1}\frac{1-x}{1+x}}{x}dx=2\ln2\int_0^1\frac{\ln^{2k-1}y}{1-y^2}dy-2\int_0^1\frac{\ln^{2k-1}y\ln(1+y)}{1-y^2}dy$$第1項は前々回の記事で求めているのでOKです。やはりきれいな式にならないので結果は書きません。
定理11の結果から、先ほどと同様にEuler-sumを導出します。交代調和数$$h_n:=1-\frac{1}{2}+\cdots+\frac{(-1)^{n-1}}{n}\;,\quad h_0=0$$はこちらの記事から$$\sum_{n=1}^\infty h_n x^n = \frac{\ln(1+x)}{1-x}$$ですので$$\sum_{n=1}^\infty\frac{h_n}{(n+1)^k}=\frac{(-1)^{k-1}}{(k-1)!}\int_0^1\frac{\ln^{k-1}x\ln(1+x)}{1-x}dx$$また$$\sum_{n=1}^\infty\frac{h_n}{(n+1)^k}=\sum_{n=1}^\infty\frac{h_n}{n^k}-\underbrace{\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^{k+1}}}_{\eta(k+1)}$$なので
$k\in\ZZ_{\ge2}$,\begin{align}\sum_{n=0}^\infty\frac{h_n}{n^k}&=k\left(1-\frac{1}{2^k}-\frac{k}{2}\right)\zeta(k+1)\\&\quad+2\left(1-\frac{1}{2^{k}}\right)\zeta(k)\ln2\\&\quad+\frac{1}{2}\sum_{r=2}^{k-1}\eta(r)\eta(k-r+1)\end{align}
次回はいよいよ本丸に切り込みます:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。