前の記事:
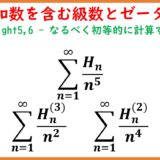
$n=0,1,2,\cdots$ に対して調和数 $H_n$ および一般化調和数 $H_n^{(p)}$ を次のように定義する。$$H_n=1+\frac{1}{2}+\cdots+\frac{1}{n}\quad,\quad H_0=0$$$$H_n^{(p)}=1+\frac{1}{2^p}+\cdots+\frac{1}{n^p}\quad,\quad H_0^{(p)}=0$$いま $n\in\NN$ とすると次が成り立つ。$$I_n:=\int_0^1 x^{n-1}\ln(1-x)dx=-\frac{H_n}{n}$$$$J_n:=\int_0^1 x^{n-1}\ln^2(1-x)dx=\frac{H_n^2+H_n^{(2)}}{n}$$$$K_n:=\int_0^1 x^{n-1}\ln^3(1-x)dx=-\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{n}$$なお補題として以下も導く。$$\sum_{k=1}^n\frac{H_k}{k} =\frac{H_n^2+H_n^{(2)}}{2}$$$$\sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k}=\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{3}$$
さらにアーベルの級数変形法:
$A_n:=\sum_{k=0}^n a_k$ とするとき$$\sum_{k=m+1}^{m+n} a_kb_k=A_{m+n} b_{m+n+1}-A_m b_{m+1}+\sum_{k=m+1}^{m+n} A_k(b_k-b_{k+1})$$
ポイントは対数のマクローリン展開:\begin{equation}\ln(1-x) =-\sum_{n=1}^\infty\frac{x^n}{n}\tag{1}\end{equation}です。
\begin{eqnarray*} I_n &=& \int_0^1 x^{n-1}\ln(1-x)dx \\&=& -\sum_{k=1}^\infty\frac{1}{k}\int_0^1 x^{n+k-1}dx \\&=& \\&=& -\sum_{k=1}^\infty\frac{1}{k(n+k)} \\&=& -\frac{1}{n}\sum_{k=1}^\infty\left(\frac{1}{k}-\frac{1}{n+k}\right)\end{eqnarray*}ここで$$\sum_{k=1}^\infty\left(\frac{1}{k}-\frac{1}{n+k}\right)=\left(1+\frac{1}{2}+\cdots\right)-\left(\frac{1}{n+1}+\frac{1}{n+2}+\cdots\right)$$すなわち\begin{equation}\sum_{k=1}^\infty\left(\frac{1}{k}-\frac{1}{n+k}\right)=H_n\tag{2}\end{equation}なので
\begin{equation}I_n:=\int_0^1 x^{n-1}\ln(1-x)dx=-\frac{H_n}{n}\tag{3}\end{equation}
次にいきましょう。部分積分のテクニックを使います。\begin{eqnarray*} J_n &=& \int_0^1 x^{n-1}\ln^2(1-x)dx \\&=& \frac{1}{n} \int_0^1 (x^n-1)'\ln^2(1-x)dx \\&=& \frac{1}{n}\left[(x^n-1)\ln^2(1-x)\right]_0^1-\frac{2}{n}\int_0^1 \frac{x^n-1}{x-1}\ln(1-x)dx \\&=& -\frac{2}{n}\int_0^1 \frac{x^n-1}{x-1}\ln(1-x)dx\end{eqnarray*}$x^n-1$ の因数分解を利用すれば$$J_n=-\frac{2}{n}\int_0^1 \left(1+x^2+\cdots+x^{n-1}\right)\ln(1-x)dx$$よって和の記号を用いると$$J_n=-\frac{2}{n}\sum_{k=1}^{n}\int_0^1 x^{k-1}\ln(1-x)dx$$(3)により\begin{equation}J_n=\frac{2}{n}\sum_{k=1}^{n}\frac{H_k}{k}\tag{4}\end{equation}右辺はEuler-sumの形に見えますが、有限和です。この場合、うまい方法でシグマを外せます。
\begin{eqnarray*}H_n^2 &=& \sum_{k=1}^n\frac{1}{k}\sum_{l=1}^n\frac{1}{l} \\&=& \sum_{k=1}^n\left(\sum_{l=1}^n\frac{1}{kl}\right)\end{eqnarray*}$l$ の和を $l=1,2\cdots,k$ と $l=k,k+1,\cdots,n$ に分けます。 $l=k$ がダブっているのでその分だけ引き算します。$$H_n^2=\sum_{k=1}^n\left(\sum_{l=1}^k\frac{1}{kl}+\sum_{l=k}^n\frac{1}{kl}-\frac{1}{k^2}\right)$$右辺の最終項は一般化調和数の定義により$$H_n^2=\sum_{k=1}^n\left(\sum_{l=1}^k\frac{1}{kl}+\sum_{l=k}^n\frac{1}{kl}\right)-H_n^{(2)}$$\begin{eqnarray*}\therefore\quad H_n^2+H_n^{(2)}&=&\sum_{k=1}^n\sum_{l=1}^k\frac{1}{kl}+\sum_{k=1}^n\sum_{l=k}^n\frac{1}{kl} \\&=& \sum_{k=1}^n\sum_{l=1}^k\frac{1}{kl}+\sum_{l=1}^n\sum_{k=1}^l\frac{1}{kl} \\&=& \sum_{k=1}^n\sum_{l=1}^k\frac{1}{kl}+\sum_{k=1}^n\sum_{l=1}^k\frac{1}{lk} \\&=& 2\sum_{k=1}^n\sum_{l=1}^k\frac{1}{kl} \\&=& 2\sum_{k=1}^n\left(\frac{1}{k}\sum_{l=1}^k\frac{1}{l}\right) \\&=& 2\sum_{k=1}^n\frac{H_k}{k}\end{eqnarray*}したがって次の関係が成り立ちます。\begin{equation}\sum_{k=1}^n\frac{H_k}{k} =\frac{H_n^2+H_n^{(2)}}{2}\tag{5}\end{equation}(4)に適用すると
\begin{equation}J_n:=\int_0^1 x^{n-1}\ln^2(1-x)dx=\frac{H_n^2+H_n^{(2)}}{n}\tag{6}\end{equation}
次に $K_n$ を計算します。先に必要な定理を紹介しておきます。アーベルの級数変形法といわれています。
$A_n:=\sum_{k=0}^n a_k$ とするとき\begin{equation}\sum_{k=m+1}^{m+n} a_kb_k=A_{m+n} b_{m+n+1}-A_m b_{m+1}+\sum_{k=m+1}^{m+n} A_k(b_k-b_{k+1})\tag{7}\end{equation}【証明】\begin{eqnarray*}a_kb_k &=& (A_k-A_{k-1})b_k \\&=& A_k(b_k-b_{k+1})+A_kb_{k+1}-A_{k-1}b_k\end{eqnarray*}和をとって$$\sum_{k=m+1}^{m+n}a_k b_k = \sum_{k=m+1}^{m+n}A_k(b_k-b_{k+1})+\sum_{k=m+1}^{m+n}\left(A_kb_{k+1}-A_{k-1}b_k\right)$$右辺の右側にある和は階差になっている。よってただちに示される。
【証明終】
(参考) K. Knopp(1971), Theory and Applications of Infinite Series, §43
特に $m=0$ とすれば\begin{equation}\sum_{k=1}^{n} a_kb_k=A_{n} b_{n+1}-a_0 b_{1}+\sum_{k=1}^{n} A_k(b_k-b_{k+1})\tag{8}\end{equation}よって $a_0=0$ のときは次のように書き直せます。
$A_n:=\sum_{k=1}^n a_k$ とするとき\begin{equation}\sum_{k=1}^n a_kb_k=A_n b_{n+1}+\sum_{k=1}^n A_k(b_k-b_{k+1})\tag{9}\end{equation}
本記事では定理そのものよりもこの系Aを使います。
では本題に入りましょう。部分積分により\begin{eqnarray*}K_n &=& \int_0^1 x^{n-1}\ln^3(1-x)dx \\&=& -\frac{3}{n}\sum_{k=1}^n\int_0^1 x^{k-1}\ln^2(1-x)dx \\&=& -\frac{3}{n}\sum_{k=1}^n J_k\end{eqnarray*}よって(6)より\begin{equation}K_n =-\frac{3}{n}\sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k}\tag{10}\end{equation}系Aで $a_k=1/k$ , $b_k=H_k^2+H_k^{(2)}$ とすると $A_k=H_k$ となるので\begin{eqnarray*} &&\sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k} \\&=& H_n\left(H_{n+1}^2+H_{n+1}^{(2)}\right)+\sum_{k=1}^n H_k\left(H_k^2+H_k^{(2)}-H_{k+1}^2-H_{k+1}^{(2)}\right) \\&=& H_n\left(H_{n+1}^2+H_{n+1}^{(2)}\right)+\sum_{k=1}^n H_k\left(-\frac{2H_k+\frac{1}{k+1}}{k+1}-\frac{1}{(k+1)^2}\right) \\&=& H_n\left(H_{n+1}^2+H_{n+1}^{(2)}\right)-2\sum_{k=1}^n\left(\frac{H_k^2}{k+1}+\frac{H_k}{(k+1)^2}\right) \\&=& H_n\left(H_{n+1}^2+H_{n+1}^{(2)}\right)-2\sum_{k=1}^n\left(\frac{H_{k-1}^2}{k}+\frac{H_{k-1}}{k^2}\right)-2\left(\frac{H_n^2}{n+1}+\frac{H_n}{(n+1)^2}\right) \\&=& H_n^3+H_nH_n^{(2)}-2\sum_{k=1}^n\left(\frac{H_{k-1}^2}{k}+\frac{H_{k-1}}{k^2}\right) \\&=& H_n^3+H_nH_n^{(2)}-2\sum_{k=1}^n\left(\frac{(H_k-\frac{1}{k})^2}{k}+\frac{H_k-\frac{1}{k}}{k^2}\right) \\&=& H_n^3+H_nH_n^{(2)}-2\sum_{k=1}^n\left(\frac{H_k^2}{k}-\frac{H_k}{k^2}\right) \end{eqnarray*}(系Aで $a_k=1/k^2$ , $b_k=H_k$ とすると)\begin{eqnarray*}&=& H_n^3+H_nH_n^{(2)}+2\left(H_n^{(2)}H_{n+1}-\sum_{k=1}^n\frac{H_k^{(2)}}{k+1}\right)-2\sum_{k=1}^n\frac{H_k^2}{k} \\&=& H_n^3+3H_nH_n^{(2)}+\frac{2H_n^{(2)}}{n+1}-2\sum_{k=1}^n\frac{H_k^{(2)}}{k+1}-2\sum_{k=1}^n\frac{H_k^2}{k} \\&=& H_n^3+3H_nH_n^{(2)}+\frac{2H_n^{(2)}}{n+1}-2\left(\frac{H_{n}^{(2)}}{n+1}+\sum_{k=1}^n\frac{H_{k-1}^{(2)}}{k}\right)-2\sum_{k=1}^n\frac{H_k^2}{k} \\&=& H_n^3+3H_nH_n^{(2)}-2\sum_{k=1}^n\frac{H_{k-1}^{(2)}+H_k^2}{k} \\&=& H_n^3+3H_nH_n^{(2)}-2\sum_{k=1}^n\left(\frac{H_k^{(2)}+H_k^2}{k}-\frac{1}{k^3}\right) \\&=& H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}-2\sum_{k=1}^n\left(\frac{H_k^{(2)}+H_k^2}{k}\right)\end{eqnarray*}$$\therefore\quad \sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k}=H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}-2\sum_{k=1}^n\left(\frac{H_k^{(2)}+H_k^2}{k}\right)$$\begin{equation}\therefore\quad\sum_{k=1}^n\frac{H_k^2+H_k^{(2)}}{k}=\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{3}\tag{11}\end{equation}(11)を(10)へ適用して
\begin{equation}K_n:=\int_0^1 x^{n-1}\ln^3(1-x)dx=-\frac{H_n^3+3H_nH_n^{(2)}+2H_n^{(3)}}{n}\tag{12}\end{equation}
・K. Knopp(1971), Theory and Application of Infinite Series
・今回の積分は、下記文献にある演習を紹介したものです[Vălean(2019), §1.3]。本書ではさらに高次のものも取り上げられています。よかったら手に取ってみてください。
本記事で参照したのは Cornel Ioan Vălean, "(Almost) Impossible Integrals, Sums, and Series" です。めちゃくちゃ難しい積分が目白押しで楽しいです。

【Amazon】(Almost) Impossible Integrals, Sums, and Series
次:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。