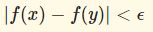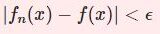一様連続とは、関数全体が同じδで押さえられる連続性です。今回はイプシロン・デルタ論法によって一様連続でないことを証明する方法を例題を使って解説します。否定を学ぶことでイプシロン・デルタ論法をより深く理解できるはずです。
そもそも一様連続とは、以下を満たす関数 $f(x)$ です。
任意の $\epsilon>0$ に対してある $\delta>0$ が存在し$$|x-y|<\delta \Rightarrow |f(x)-f(y)|<\epsilon$$とできる．
そもそも「連続って何？」「一様連続って何？」という方は、過去記事を参照ください。1つ目のリンクには「連続でないこと」の証明の例題があります。
上記の否定をとれば分かるように $f(x)$ が一様連続でないとは以下を満たすことです。
ある$\epsilon>0$ が与えられたとき、任意の $\delta>0$ について$$|x-y|<\delta かつ |f(x)-f(y)|\ge\epsilon$$なる $x , y$ が存在する。
一様連続とは「任意の $\epsilon$ に対して、ホニャララ」という構成ですから、その否定は「ある $\epsilon$ が存在して、ホニャララでない」となります。すべてについて成り立つことの否定は、１つでも成り立たないものがある、ですから。
そのホニャララというのは「ある $\delta$ が存在して、ムニャムニャ」という内容ですから、否定バージョンは"そんな $\delta$ は１つもない！"ということなので「任意の $\delta$ についてムニャムニャではない」となります。
ここまで否定バージョンをまとめると「ある $\epsilon$ が存在して、任意の $\delta$ についてムニャムニャではない」という形ができます。
で、ムニャムニャとは $|x-y|<\delta\Longrightarrow|f(x)-f(y)|<\epsilon$ すなわち「 $|x-y|<\delta$ を満たす $x,y$ はすべて$|f(x)-f(y)|<\epsilon$ を満たす」という意味ですから、その否定は「 $|x-y|<\delta$ を満たしても$|f(x)-f(y)|\ge\epsilon$ となってしまう $x,y$ が存在するよ」です。つまり任意の $\delta$ で抑えられた結果 $x,y$ どうしは十分に近いのに、$|f(x)-f(y)|$ は大きいままだというイメージです。
「一様連続でない」というのは以上のように説明できます。
$x\in\mathbb{R}$ で定義される $f(x)=x^2$ は一様連続でない。
定義域が有界であれば $x^2$ は一様連続であることは前回説明しました。
【ε論法】関数の一様連続性の証明
しかし全実数だとそうはいきません。
任意の $\delta>0$ に対し、$x=\delta/2+1/\delta$ , $y=1/\delta$ と定めます。すると $|x-y|=\delta/2<\delta$ となります。$\delta$ は任意ですから、これは $x , y$ が非常に近くできるということを意味します。ところが\begin{eqnarray*}|f(x)-f(y)|&=&|x-y||x+y|\\&=&\frac{\delta}{2}\left(\frac{\delta}{2}+\frac{2}{\delta}\right)\\&=&\frac{\delta^2}{4}+1\ge 1\end{eqnarray*}となり、$f(x)$ と $f(y)$ は1よりも近づかないので一様連続ではありません。ちゃんと書けば以下のようになるでしょう。
$\epsilon=1$ ととると、任意の $\delta>0$ について、$$|x-y|<\delta \;かつ\;|f(x)-f(y)|\ge\epsilon$$ となる $x , y $ が存在する( $x=\delta/2+1/\delta$ , $y=1/\delta$ )。よって一様連続ではない。
$x>0$ で定義される $f(x)=1/x$ は一様連続でない。
任意の $\delta>0$ に対して $N>1/\delta$ となるような適当な自然数 $N$ を定め$$x=\frac{2}{N}\quad,\quad y=\frac{1}{N}$$とします。これは $|x-y|=1/N<\delta$ を満たしています。
関数値の差を評価すると$$|f(x)-f(y)|=|\frac{N}{2}-N|=\frac{N}{2}\ge\frac{1}{2}$$つまり $\epsilon=1/2$ ととれば以下のようにいえます。
$\epsilon=1/2$ ととると、任意の $\delta>0$ について、$$|x-y|<\delta \;かつ\;|f(x)-f(y)|\ge\epsilon$$ となる $x , y $ が存在するので一様連続ではない。
$\delta$ を探す一様連続の証明とは少し視点が違っていて、今回は $\delta$ は任意でそれに対して何か1組の $x,y$ を探すという感じでした。一様連続について理解するには、一様連続の否定についてもしっかり考える必要があると思います。
【ε論法】数列の収束と極限・例題 ～εとNを使って～
【ε論法】数列がコーシー列であることの証明および収束性
【ε論法】コーシー列でないことの証明
【ε論法】関数の連続性とδのテクニック
【ε論法】関数の一様連続性の証明
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
