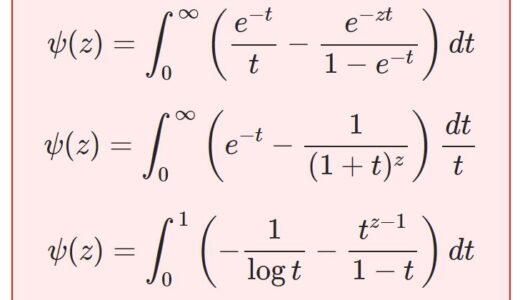「ガンマ関数の基礎」シリーズ第14回です。前回の記事は:
【γ13】ガンマ関数の放物線経路によるブルゲの積分表示・ハンケル路(ガンマ関数の基礎13)
です。読まなくても本記事を進めるのに支障ありません。
オイラー・マスケローニ定数を $\g$ とすると$$\g=\int_0^1\frac{1-e^{-t}-e^{-\frac{1}{t}}}{t}dt$$$$\g=\int_0^\infty\left(\frac{1}{1-e^{-t}}-\frac{1}{t}\right)e^{-t}dt$$が成立する。
ごちゃっとしてますが、ほぼ高校数学で初等的に理解できます。
ガンマ関数 $\G(z)$ を乗積表示したり、ディガンマ関数 $\psi(z)$ の値を表すときにこの定数 $\g$ が使われます。本シリーズではこれを次のように定義しています。
\begin{equation}\gamma\equiv\displaystyle\lim_{n\to\infty}\left(\sum_{k=1}^n\frac{1}{k}-\log n\right)\approx 0.577\tag{1}\end{equation}
これを用いて今日の積分表示を導いていきます。これらの表示はのちに、ディガンマ関数の積分表示を導出するときに有用です。オイラー・マスケローニ定数を単にオイラー定数ともよびます。
なお(1)の収束性については以下の記事をご参照:
調和数の導入
調和数 $h_n\equiv\displaystyle\sum_{k=1}^n\frac{1}{k}$ に対して\begin{equation}h_n=\int_0^1\frac{1-(1-t)^n}{t}dt\tag{2}\end{equation}が成立する。
調和数とは自然数の逆数の和であり、オイラー定数と密接な関係があります。補題を証明しましょう。
右辺の被積分関数には $1-X^n$ の形が現れています。\begin{eqnarray*}1-(1-t)^n&=&(1-1+t)\bigl[1+(1+t)+(1+t)^2+\cdots+(1+t)^{n-1}\bigr]\\&=&t\bigl[1+(1+t)+(1+t)^2+\cdots+(1+t)^{n-1}\bigr]\end{eqnarray*}したがって\begin{eqnarray*}\int_0^1\frac{1-(1-t)^n}{t}dt&=&\int_0^1\bigl[1+(1-t)+(1-t)^2+\cdots +(1-t)^{n-1}\bigr]dt\\&=&\left[t-\frac{(1-t)^2}{2}-\frac{(1-t)^3}{3}-\cdots -\frac{(1-t)^n}{n}\right]_0^1\\&=&1+\frac{1}{2}+\frac{1}{3}+\cdots+\frac{1}{n}\\&=&h_n\end{eqnarray*}よって(2)は示されました。
調和数と対数の差
ここで次の積分を考えましょう。$$\int_0^1\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}-\int_1^n\left(1-\frac{t}{n}\right)^n\frac{dt}{t}$$$\frac{t}{n}=s$ と置換すると\begin{eqnarray*}&=&\int_0^\frac{1}{n}\Bigl[1-(1-s)^n\Bigr]\frac{ds}{s}-\int_\frac{1}{n}^1(1-s)^n\frac{ds}{s}\\&=&\int_0^\frac{1}{n}\frac{1-(1-s)^n}{s}ds+\int_\frac{1}{n}^1\frac{1-(1-s)^n}{s}ds-\int_\frac{1}{n}^1\frac{1}{s}ds\\&=&\int_0^1\frac{1-(1-s)^n}{s}ds-\log n\end{eqnarray*}第1項は補題1を用いれば $h_n$ に等しいです。以上から
\begin{equation}h_n-\log n=\int_0^1\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}-\int_1^n\left(1-\frac{t}{n}\right)^n\frac{dt}{t}\tag{3}\end{equation}
nの極限をとる
(1)を見ると、補題2の極限 $n\to\infty$ をとれば $\g$ の値となることが分かります。式を変形していきましょう。
$$h_n-\log n=\int_0^1\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}-\int_1^n\left(1-\frac{t}{n}\right)^n\frac{dt}{t}$$の右辺第2項のみ $s=\dfrac{t}{n}$ と置換します。\begin{eqnarray*}h_n-\log n&=&\int_0^1\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}-\int_1^\frac{1}{n}\left(1-\frac{1}{ns}\right)^ns\frac{-ds}{s^2}\\&=&\int_0^1\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}-\int_\frac{1}{n}^1\left(1-\frac{1}{ns}\right)^n\frac{ds}{s}\\&=&\int_0^1\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}-\int_\frac{1}{n}^1\left(1-\frac{1}{nt}\right)^n\frac{dt}{t}\\&=&\int_0^\frac{1}{n}\left[1-\left(1-\frac{t}{n}\right)^n\right]\frac{dt}{t}+\int_\frac{1}{n}^1\frac{1-(1-\frac{t}{n})^n-(1-\frac{1}{nt})^n}{t}dt\end{eqnarray*}第1項の被積分関数は$$\frac{1-\left(1-\frac{t}{n}\right)^n}{t}=\frac{\frac{t}{n}\times tの多項式}{t}$$なので $n\to\infty$ で積分はゼロとなります。よってこの項を省くことができて$$\displaystyle\lim_{n\to\infty}\left(h_n-\log n\right)=\displaystyle\lim_{n\to\infty}\int_\frac{1}{n}^1\frac{1-(1-\frac{t}{n})^n-(1-\frac{1}{nt})^n}{t}dt$$左辺は $\g$ の定義そのものですので
\begin{equation}\g=\displaystyle\lim_{n\to\infty}\int_\frac{1}{n}^1\frac{1-(1-\frac{t}{n})^n-(1-\frac{1}{nt})^n}{t}dt\tag{4}\end{equation}
積分の評価
(4)をもう少し有用な形にするために次の補題が必要です。
$t>0$ において\begin{equation}0\le e^{-t}-\left(1-\frac{t}{n}\right)^n\le \frac{t^2e^{-t}}{n}\tag{5}\end{equation}
これを証明します。$0\le x<1$ に対して$$1+x\le e^x\le \frac{1}{1-x}$$が成り立ちます(中辺と右辺の級数展開から明らか)。十分大きな $n$ に対して $0<\frac{t}{n}<1$ ですから、これを $x$ に代入して$$1+\frac{t}{n}\le e^{\frac{t}{n}}\le \frac{1}{1-\frac{t}{n}}$$$n$ 乗して逆数をとると$$\left(1-\frac{t}{n}\right)^n\le e^{-t}\le \left(1+\frac{t}{n}\right)^{-n}$$$$\therefore\quad 0\le e^{-t}-\left(1-\frac{t}{n}\right)^n$$
一方、$(1-x)^n\ge 1-nx$ と仮定すると\begin{eqnarray*}(1-x)^{n+1}&\ge&(1-nx)(1-x)\\&=&1-(n+1)x+nx^2\ge 1-(n+1)x\end{eqnarray*}よって数学的帰納法により$(1-x)^n\ge 1-nx$ が成立します(ただし $nx<1$ を仮定しました。$nx\ge1$ ではこの不等式は明らかです)。十分大きな $n$ に対して $x=\frac{t^2}{n^2}$ を代入すると$$\left(1-\frac{t^2}{n^2}\right)^n\ge 1-\frac{t^2}{n}$$先ほど現れた $e^{-t}\le(1+t/n)^{-n}$ を用いて$$e^{t}\left(1-\frac{t}{n}\right)^n\ge 1-\frac{t^2}{n}$$$$\therefore\quad e^{-t}-\left(1-\frac{t}{n}\right)^n\le \frac{t^2e^{-t}}{n}$$以上で補題3は示されました。
積分表示の完成
補題3より$$0\le e^{-t}-\left(1-\frac{t}{n}\right)^n\le \frac{t^2e^{-t}}{n}$$$$0\le e^{-\frac{1}{t}}-\left(1-\frac{1}{nt}\right)^n\le \frac{e^{-\frac{1}{t}}}{nt^2}$$これにより以下の不等式が成立します。\begin{eqnarray*}&&\int_\frac{1}{n}^1\frac{1-e^{-t}-e^{-\frac{1}{t}}}{t}dt\\&\le&\int_\frac{1}{n}^1\frac{1-(1-\frac{t}{n})^n-(1-\frac{1}{nt})^n}{t}dt\\&\le&\int_\frac{1}{n}^1\frac{1-e^{-t}-e^{-\frac{1}{t}}+\frac{t^2e^{-t}}{n}+\frac{e^{-\frac{1}{t}}}{nt^2}}{t}dt\end{eqnarray*}3段目の第4項と第5項は普通に積分できて、$n\to\infty$ の極限でゼロになります。ゆえにはさみうちによって2段目は$$\displaystyle\lim_{n\to\infty}\int_\frac{1}{n}^1\frac{1-(1-\frac{t}{n})^n-(1-\frac{1}{nt})^n}{t}dt=\int_0^1\frac{1-e^{-t}-e^{-\frac{1}{t}}}{t}dt$$(4)より左辺は $\g$ ですので
\begin{equation}\g=\int_0^1\frac{1-e^{-t}-e^{-\frac{1}{t}}}{t}dt\tag{6}\end{equation}
これでオイラー定数の積分表示1つめが得られました。
(6)の積分を2つに分けて後者だけ $s=1/t$ と置換します。広義積分の下端を小さな正の数 $\epsilon$ と書き直して\begin{eqnarray*}\g&=&\int_\epsilon^1\left(\frac{1-e^{-t}}{t}-\frac{e^{-\frac{1}{t}}}{t}\right)dt\\&=&\int_\epsilon^1\frac{1-e^{-t}}{t}dt-\int^1_\infty se^{-s}\frac{-ds}{s^2}\\&=&\int_\epsilon^1\frac{1-e^{-t}}{t}dt-\int_1^\infty \frac{e^{-s}}{s}ds\\&=&\int_\epsilon^1\frac{1-e^{-t}}{t}dt-\int_1^\infty \frac{e^{-t}}{t}dt\\&=&\int_\epsilon^1\frac{dt}{t}-\int_\epsilon^\infty\frac{e^{-t}}{t}dt\end{eqnarray*}巧妙ですね。第1項の積分で $t=1-e^{-u}$ と置換すると\begin{eqnarray*}\g&=&\int_{\log\frac{1}{1-\epsilon}}^\infty\frac{e^{-u}du}{1-e^{-u}}-\int_\epsilon^\infty\frac{e^{-t}}{t}dt\\&=&\int_{\log\frac{1}{1-\epsilon}}^\epsilon\frac{e^{-u}du}{1-e^{-u}}+\int_{\epsilon}^\infty\frac{e^{-u}du}{1-e^{-u}}-\int_\epsilon^\infty\frac{e^{-t}}{t}dt\\&=&\int_{\log\frac{1}{1-\epsilon}}^\epsilon\frac{e^{-u}du}{1-e^{-u}}+\int_{\epsilon}^\infty\left(\frac{e^{-t}}{1-e^{-t}}-\frac{e^{-t}}{t}\right)dt\\&=&\left[\log(1-e^{-u})\right]_{\log\frac{1}{1-\epsilon}}^\epsilon+\int_{\epsilon}^\infty\left(\frac{e^{-t}}{1-e^{-t}}-\frac{e^{-t}}{t}\right)dt\\&=&\log\frac{1-e^{-\epsilon}}{\epsilon}+\int_{\epsilon}^\infty\left(\frac{e^{-t}}{1-e^{-t}}-\frac{e^{-t}}{t}\right)dt\end{eqnarray*}第1項に関して、平均値の定理より $0<\delta<\epsilon$ なる $\delta$ が存在して$$\frac{1-e^{-\epsilon}}{0-\epsilon}=-e^{-\delta}$$$\epsilon\to0$ なら $\delta\to0$ のため$$\frac{1-e^{-\epsilon}}{\epsilon}\rightarrow 1\quad(\mathrm{as}\; \epsilon\to0)$$$$\therefore\quad\log\frac{1-e^{-\epsilon}}{\epsilon}\rightarrow0$$以上からオイラー定数の積分表示の2つめが得られます。
$$\g=\int_0^\infty\left(\frac{1}{1-e^{-t}}-\frac{1}{t}\right)e^{-t}dt$$
以上で積分表示2つを導くことができました。すぐには思いつかないような評価方法だとか置換であったり、積分を分割したり、区間を分割したりなど、かなり技巧的な部分がありました。でもほぼ高校数学で理解できるのがすごいですね。
本記事はWhittaker-Watsonの12章を参考にして、原著を読んでもすぐには納得いかなそうなところをていねいに埋める形で進めました。
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
原著のこの部分は、定数 $\g$ そのものが目的なのではなく、ディガンマ関数を積分表示するための補助として導いています。ですので次回は、今日学んだことを生かしてディガンマ関数 $\psi(z)$ の積分表示を導出しましょう。
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。