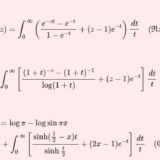【γ18】対数ガンマ関数のフーリエ級数表示（ガンマ関数の基礎18）

「ガンマ関数の基礎」シリーズ第18回です。前回の記事の続きです。前回はこちら：

【γ17】ガンマ関数のクンマーによる積分表示

前回得られた結論を出発点とし、次の等式を導出します。

クンマーの積分表示

前回、次の式を得ました。

これから右辺の積分部分を級数に変えていきます。

1-2xのフーリエ展開

を証明します。$f(x)=x$ を $x\in(-\frac{1}{2},\frac{1}{2})$ でフーリエ展開します。$f(x)$ は奇関数なので $\sin$ の項だけでいいです。$$f(x)=\sum_{n=1}^\infty a_n\sin2n\pi x$$両辺に $\sin2m\pi x$ をかけて積分します。右辺では $m=n$ の項だけ残り$$\int_{-\frac{1}{2}}^\frac{1}{2}f(x)\sin2m\pi xdx=\frac{a_m}{2}$$この左辺を計算すると $f(x)=x$ より$$\int_{-\frac{1}{2}}^\frac{1}{2}x\sin2m\pi xdx=\frac{(-1)^{m+1}}{2m\pi}$$$$\therefore\quad a_m=\frac{(-1)^{m+1}}{m\pi}$$

よって $x\in(-\frac{1}{2},\frac{1}{2})$ での $x$ のフーリエ展開は$$x=\sum_{n=1}^\infty \frac{(-1)^{n+1}}{n\pi}\sin2n\pi x$$$-2$ 倍します。$$-2x=2\sum_{n=1}^\infty \frac{(-1)^{n}}{n\pi}\sin2n\pi x$$$x$ を $x-\frac{1}{2}$ に置き換えると、$0<x<1$ において$$-2\left(x-\frac{1}{2}\right)=2\sum_{n=1}^\infty \frac{(-1)^{n}}{n\pi}\sin2n\pi\left(x-\frac{1}{2}\right)$$右辺の三角関数に加法定理を用いて$$-2\left(x-\frac{1}{2}\right)=2\sum_{n=1}^\infty \frac{\sin2n\pi x}{n\pi}$$$$\therefore\quad1-2x=2\sum_{n=1}^\infty\frac{\sin2n\pi x}{n\pi}\quad(0<x<1)$$と(1)を導出できました。

sinhのフーリエ展開

これを示します。$g(x)=\sinh tx$ を $x\in(-\frac{1}{2},\frac{1}{2})$ でフーリエ展開します。$g(x)$ は奇関数なので $\sin$ の項だけ。$$g(x)=\sum_{n=1}^\infty b_n\sin2n\pi x$$先ほどと同様にやれば$$b_n=4\int_0^\frac{1}{2}\sinh tx\sin2n\pi xdx$$となります。$b_n$ を求めましょう。

\begin{eqnarray*}\frac{b_n}{4}&=&\int_0^\frac{1}{2}\sinh tx\sin2n\pi xdx\\&=&-\frac{(-1)^n}{2n\pi}\sinh\frac{t}{2}+\frac{t}{2n\pi}\int_0^\frac{1}{2}\cosh tx\cos2n\pi xdx\\&=&-\frac{(-1)^n}{2n\pi}\sinh\frac{t}{2}-\frac{t^2}{4n^2\pi^2}\frac{b_n}{4}\end{eqnarray*}$$\therefore\quad b_n=-8\frac{(-1)^nn\pi\sinh\frac{t}{2}}{t^2+4n^2\pi^2}$$よって $x\in(-\frac{1}{2},\frac{1}{2})$ での $\sinh tx$ のフーリエ展開は$$\sinh tx=-8\sum_{n=1}^\infty \frac{(-1)^nn\pi\sinh\frac{t}{2}}{t^2+4n^2\pi^2}\sin2n\pi x$$奇関数ですので$$\sinh (-tx)=8\sum_{n=1}^\infty \frac{(-1)^nn\pi\sinh\frac{t}{2}}{t^2+4n^2\pi^2}\sin2n\pi x$$$x$ を $x-\frac{1}{2}$ に置き換えると、$0<x<1$ において$$\sinh \left(\frac{1}{2}-x\right)t=8\sum_{n=1}^\infty \frac{(-1)^nn\pi\sinh\frac{t}{2}}{t^2+4n^2\pi^2}(-1)^n\sin2n\pi x$$$$\therefore\quad\sinh\left(\frac{1}{2}-x\right)t=8\sum_{n=1}^\infty\frac{n\pi\sinh\frac{t}{2}}{t^2+4n^2\pi^2}\sin2n\pi x\quad(0<x<1)$$これで(2)を得ました。

積分項への代入

フーリエ展開(1)(2)をクンマーの積分表示の積分項に代入します。\begin{eqnarray*}&&\int_0^\infty\left[\frac{\sinh(\frac{1}{2}-x)t}{\sinh \frac{t}{2}}+(2x-1)e^{-t}\right]\frac{dt}{t}\\&=&\int_0^\infty\left[\sum_{n=1}^\infty\frac{8n\pi}{t^2+4n^2\pi^2}\sin2n\pi x-\sum_{n=1}^\infty\frac{2\sin2n\pi x}{n\pi}e^{-t}\right]\frac{dt}{t}\\&=&4\int_0^\infty\sum_{n=1}^\infty\left[\frac{2n\pi}{t^2+4n^2\pi^2}-\frac{e^{-t}}{2n\pi}\right]\sin2n\pi x\frac{dt}{t}\\&=&4\sum_{n=1}^\infty\left[\int_0^\infty\left(\frac{2n\pi}{t^2+4n^2\pi^2}-\frac{e^{-t}}{2n\pi}\right)\frac{dt}{t}\right]\sin2n\pi x\end{eqnarray*}ここで$[\quad]$ の中身を $c_n$ としましょう。$$\int_0^\infty\left[\frac{\sinh(\frac{1}{2}-x)t}{\sinh \frac{t}{2}}+(2x-1)e^{-t}\right]\frac{dt}{t}=4\sum_{n=1}^\infty c_n\sin2n\pi x$$$$c_n\equiv\int_0^\infty\left(\frac{2n\pi}{t^2+4n^2\pi^2}-\frac{e^{-t}}{2n\pi}\right)\frac{dt}{t}$$

$c_n$の計算

定義した $c_n$ を計算しましょう。$$c_n=\frac{1}{2n\pi}\int_0^\infty\left(\frac{4n^2\pi^2}{t^2+4n^2\pi^2}-e^{-t}\right)\frac{dt}{t}$$$t=2n\pi s$ と置換して$$c_n=\frac{1}{2n\pi}\int_0^\infty\left(\frac{1}{1+s^2}-e^{-2n\pi s}\right)\frac{ds}{s}$$これを用いれば\begin{eqnarray*}nc_n-c_1&=&\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+t^2}-e^{-2n\pi t}\right)\frac{dt}{t}\\&&-\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+t^2}-e^{-2\pi t}\right)\frac{dt}{t}\\&=&\frac{1}{2\pi}\int_0^\infty\frac{e^{-2\pi t}-e^{-2n\pi t}}{t}dt\\&=&\frac{1}{2\pi}\log n\end{eqnarray*}なおここで $\log$ の積分表示

を使いました。これの証明は次の記事の定理①をご覧ください：

【γ16】ビネの第1公式（導出が技巧的！）

\begin{equation}\therefore\quad nc_n-c_1=\frac{1}{2\pi}\log n\tag{3}\end{equation}

またオイラー定数 $\g$ の積分表示$$\g=\int_0^\infty\left(\frac{1}{1+t}-e^{-t}\right)\frac{dt}{t}$$を用いると

\begin{eqnarray*}c_1-\frac{\g}{2\pi}&=&\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+t^2}-e^{-2\pi t}\right)\frac{dt}{t}-\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+t}-e^{-t}\right)\frac{dt}{t}\\&=&\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+t^2}-\frac{1}{1+t}\right)\frac{dt}{t}+\frac{1}{2\pi}\int_0^\infty\frac{e^{-t}-e^{-2\pi t}}{t}dt\\&=&\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+t^2}-\frac{1}{1+t}\right)\frac{dt}{t}+\frac{1}{2\pi}\log2\pi\\&=&\frac{1}{2\pi}\int_0^\infty\left(\frac{1}{1+\frac{1}{s^2}}-\frac{1}{1+\frac{1}{s}}\right)\frac{ds}{s}+\frac{1}{2\pi}\log2\pi\;(\because s\equiv\frac{1}{t})\\&=&\frac{1}{2\pi}\int_0^\infty\left(\frac{s}{s^2+1}-\frac{1}{s+1}\right)ds+\frac{1}{2\pi}\log2\pi\\&=&\frac{1}{2\pi}\left[\frac{1}{2}\log(s^2+1)-\log(s+1)\right]_0^\infty+\frac{1}{2\pi}\log2\pi\\&=&\frac{1}{2\pi}\left[\log\frac{\sqrt{s^2+1}}{s+1}\right]_0^\infty+\frac{1}{2\pi}\log2\pi\\&=&\frac{1}{2\pi}\log2\pi\end{eqnarray*}

なお $\g$ の積分表示については次の記事の「おまけ」を参照ください：

【γ15】ディガンマ関数の積分表示３選

(3)と合わせれば$$c_n=\frac{1}{2n\pi}(\g+\log2\pi+\log n)=\frac{1}{2n\pi}(\g+\log2n\pi)$$

級数表示の完成

$$\int_0^\infty\left[\frac{\sinh(\frac{1}{2}-x)t}{\sinh \frac{t}{2}}+(2x-1)e^{-t}\right]\frac{dt}{t}=4\sum_{n=1}^\infty c_n\sin2n\pi x$$でしたから、つい先ほどの $c_n$ を代入して$$\int_0^\infty\left[\frac{\sinh(\frac{1}{2}-x)t}{\sinh \frac{t}{2}}+(2x-1)e^{-t}\right]\frac{dt}{t}=\sum_{n=1}^\infty\frac{2}{n\pi}(\g+\log2n\pi)\sin2n\pi x$$

最初の方で紹介したクンマーの積分表示\begin{multline}2\log\G(x)=\log\pi-\log\sin\pi x\\+\int_0^\infty\left[\frac{\sinh(\frac{1}{2}-x)t}{\sinh \frac{t}{2}}+(2x-1)e^{-t}\right]\frac{dt}{t}\quad(0<x<1)\end{multline}より

これで対数ガンマ関数のフーリエ級数表示ができました！ここで右辺第2項について過去記事

x^m/(sin x)^nの積分（logsinのフーリエ展開・ディリクレのベータ関数）

で得られた\begin{equation}\ln(2\sin x)=-\sum_{n=1}^\infty\frac{\cos 2nx}{n}\quad(0<x<\frac{\pi}{2})\end{equation}を用いれば

と書けます。こちらのほうが展開としては完全です。

ログガンマの積分

フーリエ級数展開がなされたことで、ログガンマの積分を考えやすくなります。例題を見てみましょう。

フーリエ級数(4)を用いることでただちに得られます。部分積分による別解もあるかもしれません。

パーセヴァルの等式を思い起こすとよいです。それを知らなくても次のように考えれば分かります。$a_0=\dfrac{\ln 2\pi}{2}$ , $a_n=\dfrac{1}{2n}$ , $b_n=\dfrac{\g+\ln2n\pi}{n\pi}$ とするとフーリエ展開は$$\ln\G(x)=a_0+\sum_{n=1}^\infty a_n\cos2n\pi x+\sum_{n=1}^\infty b_n\sin2n\pi x$$と書けます。これを2乗してばらばらにすると ①定数項　②$\cos2n\pi x$ の項　③$\sin2n\pi x$ の項　④$\cos2m\pi x\sin2n\pi x$ の項　⑤$\cos2m\pi x\cos2n\pi x$ の項($m\neq n$)　⑥$\sin2m\pi x\sin2n\pi x$ の項($m\neq n$)　⑦$\cos^22n\pi x$ の項　⑧$\sin^22n\pi x$ の項が現れます。実際に計算すると分かりますが、①⑦⑧以外はすべてゼロとなります。よって他の項は省いて$$\int_0^1\ln^2\G(x)dx=\int_0^1\left(\frac{\ln^22\pi}{4}+\sum_{n=1}^\infty\frac{\cos^22n\pi x}{4n^2}+\sum_{n=1}^\infty\frac{(\g+\ln2n\pi)^2}{n^2\pi^2}\sin^22n\pi x\right)dx$$積分を実行すると\begin{eqnarray*}&=& \frac{\ln^22\pi}{4}+\frac{\zeta(2)}{8}+\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2n\pi)^2}{n^2} \\ &=& \frac{\pi^2}{48}+\frac{\ln^22\pi}{4}+\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2\pi+\ln n)^2}{n^2}\\ &=& \frac{\pi^2}{48}+\frac{\ln^22\pi}{4}+\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2\pi+\ln n)^2}{n^2}\\&=& \frac{\pi^2}{48}+\frac{\ln^22\pi}{4}+\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2\pi)^2+2(\g+\ln2\pi)\ln n+\ln^2n}{n^2}\end{eqnarray*}ゼータ関数 $\zeta(s)=\displaystyle\sum_{n=1}^\infty\dfrac{1}{n^s}$ を微分すると$$\zeta'(s)=-\sum_{n=1}^\infty\frac{\ln n}{n^s}\;,\;\zeta''(s)=\sum_{n=1}^\infty\frac{\ln^2 n}{n^s}$$となります。これを用いれば$$\int_0^1\ln^2\G(x)dx=\frac{\pi^2}{48}+\frac{\ln^22\pi}{4}+\frac{(\g+\ln2\pi)^2}{12}-\frac{\g+\ln2\pi}{\pi^2}\zeta'(2)+\frac{\zeta''(2)}{2\pi^2}$$

例題2と全く同じ方法です。\begin{eqnarray*}\ln\G(x) &=&\frac{\ln2\pi}{2}+\frac{1}{2}\sum_{n=1}^\infty\frac{\cos2n\pi x}{n}+\frac{1}{\pi}\sum_{n=1}^\infty\frac{\g+\log2n\pi}{n}\sin2n\pi x \\\ln\G(1-x) &=&\frac{\ln2\pi}{2}+\frac{1}{2}\sum_{n=1}^\infty\frac{\cos2n\pi x}{n}-\frac{1}{\pi}\sum_{n=1}^\infty\frac{\g+\log2n\pi}{n}\sin2n\pi x\end{eqnarray*}ですので、これをかけあわせて積分すると次のものだけが残ります。$$\int_0^1\ln\G(x)\ln\G(1-x)dx=\int_0^1\left(\frac{\ln^22\pi}{4}+\sum_{n=1}^\infty\frac{\cos^22n\pi x}{4n^2}-\sum_{n=1}^\infty\frac{(\g+\ln2n\pi)^2}{n^2\pi^2}\sin^22n\pi x\right)dx$$積分を実行すると\begin{eqnarray*}&=& \frac{\ln^22\pi}{4}+\frac{\zeta(2)}{8}-\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2n\pi)^2}{n^2} \\ &=& \frac{\pi^2}{48}+\frac{\ln^22\pi}{4}-\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2\pi+\ln n)^2}{n^2}\\ &=& \frac{\pi^2}{48}+\frac{\ln^22\pi}{4}-\frac{1}{2\pi^2}\sum_{n=1}^\infty\frac{(\g+\ln2\pi)^2+2(\g+\ln2\pi)\ln n+\ln^2n}{n^2}\end{eqnarray*}$$\zeta'(s)=-\sum_{n=1}^\infty\frac{\ln n}{n^s}\;,\;\zeta''(s)=\sum_{n=1}^\infty\frac{\ln^2 n}{n^s}$$を用いれば$$\int_0^1\ln\G(x)\ln\G(1-x)dx=\frac{\pi^2}{48}+\frac{\ln^22\pi}{4}-\frac{(\g+\ln2\pi)^2}{12}+\frac{\g+\ln2\pi}{\pi^2}\zeta'(2)-\frac{\zeta''(2)}{2\pi^2}$$

$A$ はGlaisher-Kinkelin定数です。ここの定理8を参照。そのページとその前のページにはK関数について書かれており、本記事と密接に関係しています。

おわりに

本稿のなかでは $c_n$ の計算がやや技巧的で、簡単には思いつかないと思いました。フーリエ級数展開はごくごく普通の手順でしたね。今回もやはりいい計算練習となりました。

記事を書くにあたってはWhittaker-Watsonの12章12.31節のExample4を参考にしました。しかしExample4ではヒントが足りず、自力で導出できなかったのです。

古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition

そこでさらにさかのぼって、Kummerが「Journal für die reine und angewandte Mathematik」（通称：クレレ誌）のvol.35(1847年)で著した論文"Beitrag zur Theorie der Function"を読みました。

ドイツ語なので読んだというか、式だけ目で追った感じですが・・・。この論文はネットで無料で閲覧できます。

これの一番初めの論文です。$\log x$ を $l(x)$ と表記していることに気づくまで何を書いてるやら分かりませんでした。ときどきこういう古い論文を見るのも面白いですね。

次回はビネの第2公式を予定しています。その補題として「アベル・プラナの和公式」を示した記事はこちら：

2022年3月5日 アベル・プラナの和公式　複素積分を応用して

次回の記事はこちら：

【γ19】対数ガンマ関数におけるビネの第2公式の導出（アベル・プラナの和公式,ポリガンマ関数）（ガンマ関数の基礎19）

シリーズを第1回から学ぶ場合はこちら：

2022年2月7日 【γ1】ガンマ関数の定義・特殊値・解析接続・留数（ガンマ関数の基礎1）

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。