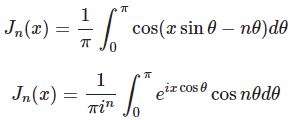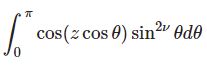ルジャンドル多項式（より一般にはルジャンドル関数）にはいろいろな表現があり，積分表示もその１つです．今日はラプラスの積分表示といわれるものを導出します．とある簡単な定積分から母関数を導いて無限級数を比較するという手法です．
\begin{equation}P_n(x)=\frac{1}{\pi}\int^\pi_0(x\pm\sqrt{x^2-1}\cos\theta)^nd\theta\tag{1}\end{equation}
$P_n(x)$ はルジャンドル多項式です．これがそもそも何なのかは過去記事を参照ください．
級数展開でルジャンドル多項式を得られるという有名な等式があります．
\begin{equation}\sum_{n=0}^\infty P_n(x)t^n=\frac{1}{\sqrt{1-2xt+t^2}}\tag{2}\end{equation}
物理でときどき使う式です．右辺を母関数といいます．証明したいところですが本旨とそれるので今はこれを認めておきます．
さて本題に入る前に準備として次の定積分の式を示しておきます．
\begin{equation}\int_0^\pi\frac{d\theta}{a\pm b\cos\theta}=\frac{\pi}{\sqrt{a^2-b^2}}\quad (a^2>b^2)\tag{3}\end{equation}
方法はいろいろあるのですがワイエルシュトラス置換を用いることにします．この置換に関する参考記事は
$\tan\displaystyle\frac{\theta}{2}=t$ とおくと$$\cos x =\frac{1-t^2}{1+t^2}\;,\;dx=\frac{2dt}{1+t^2}$$と書き直せるので\begin{eqnarray*}\int_0^\pi\frac{d\theta}{a\pm b\cos\theta}&=&\int_0^\infty \frac{1}{a\pm b\frac{1-t^2}{1+t^2}}\frac{2dt}{1+t^2}\\ &=& \int_0^\infty \frac{2dt}{a+at^2\pm b\mp bt^2}\\ &=& \int_0^\infty \frac{2dt}{a\pm b+(a\mp b)t^2}\\ &=& \frac{\pi}{\sqrt{a^2-b^2}}\end{eqnarray*} でOKです．
(3)において $a=1-tx$ , $b=t\sqrt{x^2-1}$ とすると $a^2-b^2=1-2tx+t^2$ となるので$$ \frac{\pi}{\sqrt{1-2tx+t^2}}=\int_0^\pi \frac{d\theta}{1-tx\pm t\sqrt{x^2-1}\cos\theta}$$(2) により\begin{equation} \sum_{n=0}^\infty P_n(x)t^n =\frac{1}{\pi} \int_0^\pi \frac{d\theta}{1-tx\pm t\sqrt{x^2-1}\cos\theta} \tag{4}\end{equation}
右辺の積分は\begin{eqnarray*}&&\int_0^\pi \frac{d\theta}{1-tx\pm t\sqrt{x^2-1}\cos\theta}\\&=& \int_0^\pi \frac{d\theta}{1-(x\pm \sqrt{x^2-1}\cos\theta)t} \\&=& \int_0^\pi\left[1+(x\pm \sqrt{x^2-1}\cos\theta)t+( x\pm \sqrt{x^2-1}\cos\theta )^2t^2\cdots\right]d\theta\\&=& \int_0^\pi\sum_{n=0}^\infty ( x\pm \sqrt{x^2-1}\cos\theta )^nt^nd\theta\\&=& \sum_{n=0}^\infty t^n \int_0^\pi ( x\pm \sqrt{x^2-1}\cos\theta)^nd\theta \end{eqnarray*}よって(4)は$$\sum_{n=0}^\infty P_n(x)t^n= \frac{1}{\pi} \sum_{n=0}^\infty t^n \int_0^\pi ( x\pm \sqrt{x^2-1}\cos\theta)^nd\theta $$両辺が $t$ の無限級数であり，比べると \begin{equation}P_n(x)=\frac{1}{\pi}\int^\pi_0(x\pm\sqrt{x^2-1}\cos\theta)^nd\theta\end{equation}
これでLaplaceの積分表示を示せました！
ルジャンドル多項式について見てきましたが『岩波数学公式III』によると，多項式のみならず一般のルジャンドル関数 $P_\nu(x)$ でも成立するそうです．時間を見つけて検討したいと思います．
これとは別に「シュレーフリの積分表示」というものもあります：
ベッセル関数の積分表示は本サイトで人気があるようです：
特殊関数については「ガンマ関数の基礎」シリーズ全20回があります。第1回は：
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
