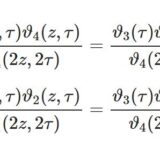前回はこちら：
テータ関数８～ワイエルシュトラスのシグマ・ゼータ関数や楕円関数との関係
楕円関数シリーズの一覧はこちらから：
テータ関数における $\tau$ は $\Im\tau>0$ を満たすのでした。テータ関数は二重の擬周期 $1,\tau$ をもちます。前回でみたように、周期 $\o_1,\o_2$ の楕円関数等とテータ関数を関連付けるときには、$\tau=\o_2/\o_1$ としました。
ペー関数のときにも説明しましたが、周期を $\o_2,-\o_1$ に取り換えても楕円関数は変わりません。これはテータ関数でいうと $\tau$ を $-1/\tau$ に取り換えることに相当します。
そこで $\tau':= -1/\tau$ と定義します。複素数の簡単な計算により $\Im\tau'>0$ ですから、この $\tau'$ を擬周期とするテータ関数を考えることができます。$q':=e^{\pi i\tau'}$ と書くことにしましょう。
このようにタウを変えることでテータ関数はどう変わるのでしょうか。零点に注目しましょう。
$\vartheta_3(z,\tau)$ は整関数であり、$z\equiv \frac{1+\tau}{2}$ にのみ1位の零点をもつのでした（$\equiv$ は合同な点という意味）。一方 $\tau'$ で成るテータ関数については、その無限積表示から\begin{equation}\vartheta_3(\tau'z,\tau')=\prod_{n=1}^\infty(1-(q')^{2n})\prod_{n=1}^\infty\left(1+(q')^{2n-1}e^{2\pi i\tau'z}\right)\left(1+(q')^{2n-1}e^{-2\pi i\tau'z}\right)\tag{1}\end{equation}(1)の零点は$$e^{\pi i\tau'(2n-1\pm 2z)}=-1\quad (n\in\NN)$$を満たす $z$ すべてです。したがって$$\pm z=n-\frac{1}{2}+\left(N+\frac{1}{2}\right)\tau\quad(n\in\NN\;,\;N\in\ZZ)$$なので結局 $z\equiv \frac{1+\tau}{2}$ が(1)の零点となります。
というわけで $\vartheta_3(z,\tau)$ と $\vartheta_3(\tau'z,\tau')$ の零点は一致します。偶関数であることから後者を $\vartheta_3(-\tau'z,\tau')$ としてもOK。
$\vartheta_3(z,\tau)$ と $\vartheta_3(-\tau'z,\tau')$ の零点は一致して $z\equiv \frac{1+\tau}{2}$ である。ただし $\tau\tau'=-1$ である。
あらたに次の関数を定義します。\begin{equation}\psi(z):=\exp\left(-\frac{\pi i}{\tau}z^2\right)\frac{\vartheta_3\left(\frac{z}{\tau},-\frac{1}{\tau}\right)}{\vartheta_3(z,\tau)}\tag{2}\end{equation}補題１よりこの関数は極も零点ももちません。
次に $\psi(z)$ の周期性を確認します。$$\psi(z+1)=\exp\left(-\frac{\pi i}{\tau}(z^2+2z+1)\right)\frac{\exp(\frac{\pi i}{\tau}+\frac{2\pi i}{\tau}z)\vartheta_3\left(\frac{z}{\tau},-\frac{1}{\tau}\right)}{\vartheta_3(z,\tau)}$$\begin{equation}\therefore\quad\psi(z+1)=\psi(z)\tag{3}\end{equation}また擬周期性の公式\begin{equation}\vartheta_3(z+\tau,\tau)=e^{-\pi i\tau-2\pi iz}\vartheta_3(z,\tau)\tag{4}\end{equation}を使えば\begin{align}\psi(z+\tau)&=\exp\left(-\frac{\pi i}{\tau}(z^2+2\tau z+\tau^2)\right)\frac{\vartheta_3\left(\frac{z}{\tau}+1,-\frac{1}{\tau}\right)}{\vartheta_3(z+\tau,\tau)}\\&=\exp\left(-\frac{\pi i}{\tau}(z^2+2\tau z+\tau^2)\right)\frac{\vartheta_3\left(\frac{z}{\tau},-\frac{1}{\tau}\right)}{e^{-\pi i\tau-2\pi iz}\vartheta_3(z,\tau)}\end{align}\begin{equation}\therefore\quad\psi(z+\tau)=\psi(z)\tag{5}\end{equation}
(3)(5)より $\psi(z)$ は二重周期 $1,\tau$ をもつことになります。しかし極をもたない二重周期関数は定数に限ります。\begin{equation}\psi(z)=A\quad(A:\mathrm{const.\:independent\:of\:}z)\tag{6}\end{equation}よって、$A$ の値はあとで求めるとして\begin{equation}\vartheta_3\left(\frac{z}{\tau},-\frac{1}{\tau}\right)=A\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_3(z,\tau)\tag{7}\end{equation}(7)で $z\to z-\frac{1}{2}$ として$$e^{\frac{\pi i}{4\tau}}e^{-\pi i\frac{z}{\tau}}\vartheta_2\left(\frac{z}{\tau},-\frac{1}{\tau}\right)=A\exp\left(\frac{\pi i}{\tau}\left(z^2-z+\frac{1}{4}\right)\right)\vartheta_4(z,\tau)$$\begin{equation}\therefore\quad\vartheta_2\left(\frac{z}{\tau},-\frac{1}{\tau}\right)=A\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_4(z,\tau)\tag{8}\end{equation}のように別の公式も得られます。
同様に(7)で $z\to z-\tau/2$ として$$e^{-\frac{\pi i\tau}{4}}e^{-\pi i(z-\frac{\tau}{2})}\vartheta_4\left(\frac{z}{\tau},-\frac{1}{\tau}\right)=A\exp\left(\frac{\pi i}{\tau}\left(z^2-\tau z+\frac{\tau^2}{4}\right)\right)\vartheta_2(z,\tau)$$\begin{equation}\therefore\quad\vartheta_4\left(\frac{z}{\tau},-\frac{1}{\tau}\right)=A\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_2(z,\tau)\tag{9}\end{equation}次に(8)で $z\to z-\tau/2$ として同様の計算をすると\begin{equation}\vartheta_1\left(\frac{z}{\tau},-\frac{1}{\tau}\right)=-i A\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_1(z,\tau)\tag{10}\end{equation}
$A$ を求めるために $z=0$ とした場合を考えてみましょう。(7)(8)(9)は\begin{align}\vartheta_3(-1/\tau)&=A\vartheta_3(\tau)\tag{11}\\\vartheta_2(-1/\tau)&=A\vartheta_4(\tau)\\\vartheta_4(-1/\tau)&=A\vartheta_2(\tau)\end{align}辺々かけると$$\vartheta_2(-1/\tau)\vartheta_3(-1/\tau)\vartheta_4(-1/\tau)=A^3\vartheta_2(\tau)\vartheta_3(\tau)\vartheta_4(\tau)$$こちらで求めたテータ定数の関係式$$\vartheta_1'=\pi\: \vartheta_2\vartheta_3\vartheta_4$$を両辺に用いると\begin{equation}\vartheta_1'(-1/\tau)=A^3\vartheta_1'(\tau)\tag{12}\end{equation}一方(10)についてはそのまま $z=0$ としてしまうと両辺がゼロになって使えません。そこで $z$ で微分してから $z=0$ とすると\begin{equation}\frac{1}{\tau}\vartheta_1'(-1/\tau)=-i A\vartheta_1'(\tau)\tag{13}\end{equation}(12)(13)から\begin{equation}A^2=-i\tau\tag{13}\end{equation}$\Im\tau >0$ でしたから $0<\arg\tau<\pi$ です。よって$$-\frac{\pi}{2}<\arg(-i\tau)<\frac{\pi}{2}$$であって$$A=\pm\tau^{1/2}e^{-\frac{\pi i}{4}}$$これで $A$ が2つの値をとるように見えますが(11)で $\tau=i$ として $A= +1$ となることから\begin{equation}A=e^{-\frac{\pi i}{4}}\tau^{1/2}\tag{14}\end{equation}に絞られます。
以上より
\begin{align}\vartheta_3\left(\frac{z}{\tau},-\frac{1}{\tau}\right)&=e^{-\frac{\pi i}{4}}\tau^{1/2}\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_3(z,\tau)\\\vartheta_2\left(\frac{z}{\tau},-\frac{1}{\tau}\right)&=e^{-\frac{\pi i}{4}}\tau^{1/2}\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_4(z,\tau)\\\vartheta_4\left(\frac{z}{\tau},-\frac{1}{\tau}\right)&=e^{-\frac{\pi i}{4}}\tau^{1/2}\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_2(z,\tau)\\\vartheta_1\left(\frac{z}{\tau},-\frac{1}{\tau}\right)&=-ie^{-\frac{\pi i}{4}}\tau^{1/2}\exp\left(\frac{\pi i}{\tau}z^2\right)\vartheta_1(z,\tau)\end{align}
目標としていたヤコビの虚数変換式を導出できました。
第５版です。いわずと知れた名著。楕円関数にかなりのページを割いています。
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。