前回は
等速円運動からはじめて,一般の円運動の方程式をマスターしよう.円運動する物体にはどのような力がはたらいているのだろうか?微分ができればこわくない!

今日は円運動について,運動方程式で表現して解いていくよ!

高校では等速円運動を基本としていたな.速さ $v$ に比例する量として角速度 $\omega$ が重要だった.等速であれば角度変化も一定だから $\omega$ は定数だ.

そうなんだ.で,このとき力は円の中心を向いていたんだよね.向心力というよ。
等速円運動であれば向心力がはたらいていることを微積で証明しよう!

$\boldsymbol{F}=m\boldsymbol{a}$ を $x,y$ の成分でそれぞれ考えればいいな.

ベクトルの成分表示が横に長くならないように,縦に並べることもあるから先に行っておくよ。こういうのを「列ベクトル」っていうんだ。
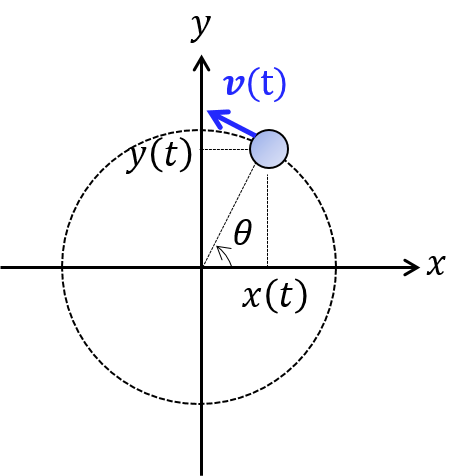
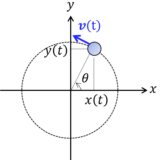
上図のように座標を設定する.時刻$0$の物体の位置が $x$ 軸上になるようにしたとする.等速円運動であれば $\theta(t)=\omega t$ だから\begin{equation}\boldsymbol{r}(t)=\left(\begin{matrix}x(t)\\y(t)\end{matrix}\right)= \left(\begin{matrix}R\cos\omega t\\R\sin\omega t\end{matrix}\right)\tag{1}\end{equation}微分すると\begin{equation}\boldsymbol{v}(t)= \left(\begin{matrix}v_x(t)\\v_y(t)\end{matrix}\right)= \left(\begin{matrix}-R\omega\sin\omega t\\R\omega\cos\omega t\end{matrix}\right)\tag{2}\end{equation}再度微分すると\begin{equation} \boldsymbol{a}(t)= \left(\begin{matrix}a_x(t)\\a_y(t)\end{matrix}\right)= \left(\begin{matrix}-R\omega^2\cos\omega t\\-R\omega^2\sin\omega t\end{matrix}\right)\tag{3}\end{equation}
これらからさまざまな等式を導出しよう.
まず速さ $v$ は $$v=|\boldsymbol{v}|=\sqrt{v_x^2+v_y^2}=R\omega$$よって周期は$$T=\frac{2\pi R}{v}=\frac{2\pi}{\omega}$$加速度の大きさは$$a= \sqrt{a_x^2+a_y^2}=R\omega^2$$また(1)と(3)より\begin{equation}\boldsymbol{a}(t)=-\omega^2\boldsymbol{r}\tag{4}\end{equation}であり,加速度ベクトルが中心方向を向いていることを示す.
さて運動方程式より$$\boldsymbol{F}=m\boldsymbol{a}= -m\omega^2\boldsymbol{r}$$よって力は中心方向を向いており,その大きさは$$F=| -m\omega^2\boldsymbol{r} |= mR\omega^2$$この力を向心力とか中心力とよんでいる.

知っている公式が芋づる式に現れたな.
でもこれまでの話と違って運動方程式を出発点にしなかったな.代わりに等速円運動の座標を $t$ で表すことからスタートして,「等速円運動であれば力は中心を向いている」という結論だ.

大人の事情があるんだ.「中心力である」という条件だけで運動方程式を立てると解きづらい微分方程式になるし,初期条件によっていろんな運動が実現してしまうんだ.円運動にするには作為的な初期条件を与えることになって,すっきりしないかもしれなかったからね.

ぼくから練習問題を出すよ!がんばってね!
$$\boldsymbol{r}(t)=\left(\begin{matrix}2\cos3 t-5\\2\sin 3t\end{matrix}\right)$$と表される物体はどのような運動をしているか.また,加速度の大きさ $a$ を求めよ.
式の形から,この物体は$(-5,0)$ を中心に半径 $2$ ,角速度 $3$ の等速円運動をしている.加速度は2階微分だから$$ \boldsymbol{a}(t)=-18\left(\begin{matrix}\cos3 t\\\sin 3t\end{matrix}\right)$$これの絶対値をとることで加速度の大きさは $a=18$ .
$$\boldsymbol{r}(t)=\left(\begin{matrix}2\cos3 t+t\\2\sin 3t\end{matrix}\right)$$と表される物体はどのような運動をしているか. また例題1とかかる力のベクトルは同じであることを簡単に説明せよ.
中心が $(t,0)$ だから時間とともに右へ移動していく.すなわち「らせん」っぽい運動をする.
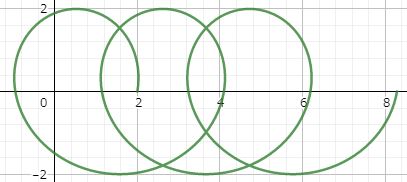
加速度は $$ \boldsymbol{a}(t)=-18\left(\begin{matrix}\cos3 t\\\sin 3t\end{matrix}\right)$$で例題1と同じである.よって質量を $m$ とすれば力 $ \boldsymbol{F}(t) =m \boldsymbol{a}(t)$ も同じである.

ある意味向心力といえるかもしれないけど,中心が右へずれていくよ.物体の位置を適当に決めて力を書いてみて。同じ運動方程式でも運動の様子が違うね。

非等速の場合も同じように先に座標を $t$ で表してから微分微分でどんな力がはたらいているかを求めればいいわけだ.

その通りさ.やることは同じってこと.非等速だから角速度 $\omega$ が時間によって変化するんだ.でもそれだけさ.微分がちょいややこしくなるだけだよ!
あ,ここで先に確認しておきたいことがあるんだ.
角速度は単位時間あたりの角度の変化だから角度の時間微分である.$$\omega =\frac{d\theta}{dt}\equiv\dot{\theta}$$

これが $\theta$ と $\omega$ の関係だよ.位置と速度の関係と同じだね.あと微分の表記が面倒だから時間微分は上にドットをつけて表現するよ!

つまり $v=\dot{x}$ とかも書けるわけだ.便利だな.
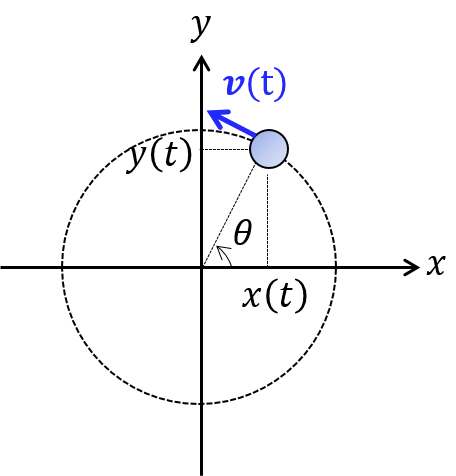
等速のときは定数 $\omega$ を使って $\theta=\omega t$ と書けたが,非等速の場合は $\theta$ がどのように時間変化するかはさまざまである.よって単に $\theta(t)$ と考えるほかない.
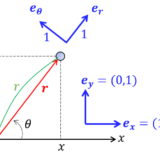
円運動であれば原点からの距離は $R$ で一定だから\begin{equation}\boldsymbol{r}(t)=R \left(\begin{matrix}\cos\theta\\\sin\theta\end{matrix}\right)\tag{5}\end{equation}$t$ で微分すると\begin{equation}\boldsymbol{v}(t)=R\left(\begin{matrix}-\dot{\theta}\sin\theta\\\dot{\theta}\cos\theta\end{matrix}\right)\tag{6}\end{equation}合成関数の微分だから $\dot{\theta}$ がかけられていることに注意.再度微分すると\begin{equation} \boldsymbol{a}(t)= R{\dot{\theta}}^2\left(\begin{matrix}-\cos\theta\\-\sin\theta\end{matrix}\right)+R\ddot{\theta} \left(\begin{matrix}-\sin\theta\\\cos\theta\end{matrix}\right) \tag{7}\end{equation} よってかかる力は \begin{equation} \boldsymbol{F}(t)= -mR{\dot{\theta}}^2\left(\begin{matrix}\cos\theta\\\sin\theta\end{matrix}\right)+mR\ddot{\theta} \left(\begin{matrix}-\sin\theta\\\cos\theta\end{matrix}\right) \tag{8}\end{equation}
式(8)は2つのベクトルの足し算となっている.第1項は,(5)を見比べることにより円の中心向きであると分かる(向心力).第2項は,(6)と見比べることにより速度方向(進む方向)であると分かる.すなわちこの力を分解すると
円の中心方向に$$F_r=mR\omega^2$$角度が増える方向(反時計回り)に$$F_\theta =mR\dot{\omega}$$ただし $\omega =\dot{\theta}$ を用いた.
$F_r$ は向心力で,円運動を保つための力である(等速円運動の式と同じ).
$F_\theta$ は何だろう?$F_\theta=0$ とすると $\dot{\omega}=0$ なので角速度は定数すなわち等速円運動である.もし $F_\theta>0$ なら $\dot{\omega}>0$ つまり角速度は増加すなわちスピードアップするわけだ.よって $F_\theta$ は円運動のスピード(正確には角速度)を変化させる力である.

合成関数の微分を忘れないようにしよう.理解するには力を2つにわけて考えることが重要だな.等速のときとやってることは同じだ.2回微分して加速度出して力を表すだけだ.

そうなんだ.円運動さらには今後学んでいく中心力という力を考えるときは極座標をとって,ベクトルも $r$ 方向と $\theta$ 方向に分解して考えると整理しやすいよ.$x,y$ でやってしまうと式がごちゃっとするんだ.

また登場だよ!非等速のほうも例題に取り組もう!正確な微分を心掛けてね。
$$\boldsymbol{r}(t)=\left(\begin{matrix}3\cos t^2\\3\sin t^2\end{matrix}\right)$$と表される物体はどのような運動をしているか.また,かかっている力を求め,向心力と速度方向に分解せよ. 物体の質量を $1$ とする.
常に $r=3$ であるから半径$3$の円運動をしている.ただし $\theta(t)=t^2$ だから角速度は $\omega=2t$ となり,等速ではなく速さはアップしていく.
$t$ で微分すると$$\boldsymbol{v}(t)=3\left(\begin{matrix}-2t\sin t^2\\2t\cos t^2\end{matrix}\right)=6t \left(\begin{matrix}-\sin t^2\\\cos t^2\end{matrix}\right) $$ $$\boldsymbol{a}(t)=12t^2 \left(\begin{matrix}-\cos t^2\\-\sin t^2\end{matrix}\right) +6 \left(\begin{matrix}-\sin t^2\\\cos t^2\end{matrix}\right) $$ 質量$1$よりかかる力は$$ \boldsymbol{F}(t)=12t^2 \left(\begin{matrix}-\cos t^2\\-\sin t^2\end{matrix}\right) +6 \left(\begin{matrix}-\sin t^2\\\cos t^2\end{matrix}\right) $$第1項は円の中心向きでその大きさは$$F_r=12t^2$$第2項は速度方向でその大きさは$$F_\theta=6$$

中心方向と速度方向にまとめるときは,$\cos$ と $\sin$ の組でベクトルを整理するといいよ!そうすると $\sqrt{\cos^2 A+\sin^2 A}=1$ で必ず大きさ$1$になるからね。大きさ1のベクトルを「単位ベクトル」というよ.とっても大事だから知っておいてね!
あと、さっきは「中心方向」に分解したけど,一般的にはその逆で外向きのベクトルにするんだ.これを「動径方向」というよ.「速度方向」も一般的には「角度方向」というよ.
微積分と高校物理シリーズ
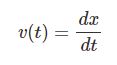
【H1】力学の表現と本シリーズの意義
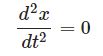
【H2】力がゼロの運動方程式と等速直線運動
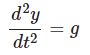
【H3】落体運動の法則はただ1つ

【H4】ばねの微分方程式 水平・鉛直・空気抵抗
【H5】等速・非等速円運動と微分方程式
【H6】ベクトルの極座標成分
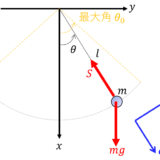
【H7】単振り子の方程式と厳密解
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。