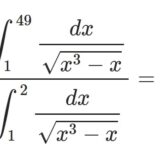@penta_math さんの出題です。
$$\int_0^1 \sqrt{x^3-5x^2+4x}\:dx=\frac{4}{15}\left[26E\left(\frac{1}{2}\right)-21K\left(\frac{1}{2}\right)\right]$$
楕円積分をルジャンドルの標準形に直して完全楕円積分に帰着させます。その練習としてものすごく適した問題だと感じ、久々にTwitterの出題に取り組みました。
こちらで一般的な話を扱っています。これにそって愚直にやるのみ。
$$I:=\int_0^1 \sqrt{x^3-5x^2+4x}\:dx$$とおいておきます。この積分において$$x=T(z)=\frac{Az+B}{Cz+D}$$の変換を考えます。$$x^3-5x^2+4x=x(x-1)(x-4)$$と因数分解されることから、次のように狙いを定めます。\begin{align}T(1)&=\infty\\T(-1)&=0\\T(1/k)&=1\\T(-1/k)&=4\end{align}これらを満たす $A,B,C,D,k$ を探します。
その結果\begin{align}T(z)&=\frac{2z-2}{(2-\sqrt{3})z-(2+\sqrt{3})}\tag{1}\\ k&= (2-\sqrt{3})^2\tag{2}\end{align}と求まります。これによって $x=T(z)$ の置換をすると\begin{equation}I=24k^{3/2}\int_{-1}^1\frac{(1-z^2)(1+kz)}{(1-kz)^3}\frac{dz}{\sqrt{(1-z^2)(1-k^2z^2)}}\tag{3}\end{equation}これで根号内が扱いやすい4次式になりました。
(3)式の根号以外の部分を部分分数分解します。\begin{equation}I=24k^{3/2}\left[\frac{1}{k^2}I_0+\frac{4}{k^3}J_1+\frac{5-k^2}{k^4}J_2+\frac{2(1-k^2)}{k^5}J_3\right]\tag{4}\end{equation}ただし、ここで\begin{align}I_n &=\int_{-1}^1\frac{z^n}{\sqrt{(1-z^2)(1-k^2z^2)}}dz\tag{5}\\J_n &=\int_{-1}^1\frac{dz}{(z-\frac{1}{k})^n\sqrt{(1-z^2)(1-k^2z^2)}}\tag{6}\end{align}これらについては次の関係式が成り立ちます。\begin{align}J_3 &=\frac{k}{5(1-k^2)}\left[2(k^2-5)J_2-6kJ_1-k^2I_0\right]\tag{7}\\J_2 &=\frac{k}{3(1-k^2)}\left[(k^2-5)J_1-2kI_0\right]\tag{8}\\J_1 &=\frac{k}{1-k^2}(k^2I_2-I_0)\tag{9}\end{align}(7)(8)(9)を(4)に用いると\begin{equation}I=\frac{2-\sqrt{3}}{15}\left[14I_0-26(7-4\sqrt{3})I_2\right]\tag{10}\end{equation}これで標準形にできました。(10)へ至る計算はなかなか面倒です。
(10)式を完全楕円積分で表現する。偶関数であることも考慮して\begin{align}I_2&=\frac{2}{k^2}\left[K(k)-E(k)\right]\tag{11}\\I_0 &=2K(k)\tag{12}\end{align}これらを(10)に適用することにより\begin{equation}I=\frac{4}{15}\left[13(2+\sqrt{3})E(k)-(12+20\sqrt{3})K(k)\right]\tag{13}\end{equation}これで終わりでもいいのですが、ちょっとキタナイ。
そこで上昇変換を施すときれいになります。\begin{align}K(7-4\sqrt{3})&=\frac{2+\sqrt{3}}{4}K\left(\frac{1}{2}\right)\tag{14}\\E(7-4\sqrt{3})&=2(2-\sqrt{3})E\left(\frac{1}{2}\right)+\sqrt{3}(2-\sqrt{3})K\left(\frac{1}{2}\right)\tag{15}\end{align}(14)(15)を(13)に用いて
$$\int_0^1 \sqrt{x^3-5x^2+4x}\:dx=\frac{4}{15}\left[26E\left(\frac{1}{2}\right)-21K\left(\frac{1}{2}\right)\right]$$
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。