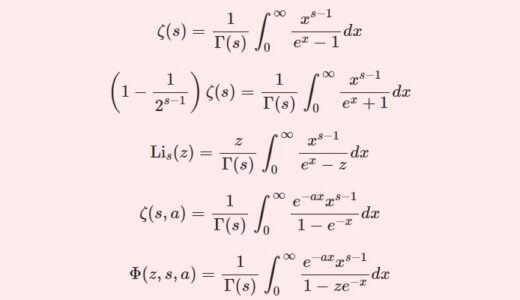もくじ
「ゼータ関数の基礎」シリーズ初回です。本シリーズではWhittaker-Watsonの13章を参考にしており、その行間をなるべく埋めて分かりやすく解説することを目指しています。その本は計算過程が省略されていたりするので。
似たようなコンセプトで「ガンマ関数の基礎」シリーズ全20回も書きました。第1回はこちら:
古いですが有名な書物で、どんどん改訂版が出ています。前半は解析学一般、後半は特殊関数という内容で、網羅的に勉強できます。演習問題に解答がないのが昔ながらのものって感じ。2022/11/6現在、最新版は5th Editionで私も所有していますが、廉価な3rdとかでも十分かと。

A Course of Modern Analysis: fifth Edition

A Course of Modern Analysis: Third Edition
フルヴィッツゼータ関数を基本とする
ゼータ関数、とりわけリーマンゼータ関数$$\zeta(s)=\sum_{n=1}^\infty\frac{1}{n^s}$$は定義が非常にシンプルでありながら大変興味深い特殊関数です。なので数学好きの間では人気で、それに関する数学ブログの記事も多いです。
しかしここで始める「ゼータ関数の基礎」シリーズではWhittaker&Watsonにならい、フルヴィッツゼータ関数を基本として進めていきます。$$\zeta(s,a)=\sum_{n=0}^\infty\frac{1}{(n+a)^s}$$というのはリーマンゼータ関数はフルヴィッツゼータ関数の特別な場合 $(a=1)$ であり、比較的浅めの学びにおいてはフルヴィッツゼータが分かればリーマンゼータも分かるからです。もちろんリーマンゼータに限定して深くつき詰めるという方向性もあるのですが(素数の話とか)、私自身が関数の特殊値や留数、積分表示などへの興味のほうが強いというのもあり、数論のような分野に入る予定はありません。なのでほとんど解析学に寄せた内容になると思います。
リーマンゼータ関数、フルヴィッツゼータ関数、レルヒの超越関数、多重対数関数(ポリログ)については過去に初等的な記事を書いています。ガンマ関数を絡めた積分表示についてです。こちらをどうぞ:
こういった知識を用いて、やや難解な積分へ応用した記事はこちら:
$\int\frac{x^m}{\sinh x}dx,\int\frac{x^m}{\cosh x}dx$ ゼータとベータ
リーマンゼータ関数の偶数における値
リーマンゼータ関数 $\zeta(s)$ は $s$ が正の偶数のときの値がよく知られています。たとえば$$\zeta(2)=\frac{\pi^2}{6}$$です。フーリエ級数展開による方法、パーセヴァルの等式による方法、$\sin$ の無限乗積による方法について解説した記事はこちらにあるので参考にしてください:
ゼータ関数値の求め方3選(フーリエ級数・パーセヴァルの等式・sin無限乗積)
ガンマ関数の微分やポリガンマ関数でも登場する
ガンマ関数の基礎シリーズで、ガンマ関数の微分とゼータ関数の関係を示した記事はこちらです:
リーマンゼータ関数はディガンマ関数の母関数ですので、その級数展開で現れます。その記事はこちら:
【γ9】ディガンマ関数の相反公式・倍数公式と特殊値・ゼータ関数(ガンマ関数の基礎シリーズ9)
ポリガンマ関数とゼータ関数の関係についてはこちら:
【γ10】ポリガンマ関数の値、極、級数表示、ゼータ関数との関係(ガンマ関数の基礎シリーズ10)
対数正弦積分にゼータ関数の値を利用する
$(\log\sin x)^n$ を定積分するときにリーマンゼータ関数の値を用います。その記事はこちら:
以上、過去記事も参考いただければと思います。
前置きが長くなりました。本記事の目標はこれです。
フルヴィッツゼータ関数\begin{equation}\zeta(s,a)=\sum_{n=0}^\infty\frac{1}{(n+a)^s}\quad(\mathfrak{R}s>1,0<a\le1)\tag{1}\end{equation}に対し、次の積分表示が成立する。\begin{equation}\zeta(s,a)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{-ax}}{1-e^{-x}}dx\tag{2}\end{equation}
フルヴィッツゼータ関数とリーマンゼータ関数の関係は明らかに $\zeta(s,1)=\zeta(s)$ です。なのでこの式はリーマンゼータ関数の積分表示も兼ねています。過去記事に同様のものがありますが、もう少し厳密にやろうと思います。
なお $a$ の値を制限していますが、たとえば $a=2$ だと$$\zeta(s,2)=\sum_{n=0}^\infty\frac{1}{(n+2)^s}=\sum_{n=1}^\infty\frac{1}{(n+1)^s}=\zeta(s,1)-1$$と結局 $a=1$ に帰着されてしまうので省いているのです。
さらにはその亜種である
$$(1-2^{1-s})\zeta(s)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}}{e^x+1}dx$$$$\zeta (s)=\frac{2^s}{(2^s-1)\G(s)}\int_0^\infty\frac{x^{s-1}e^{x}}{e^{2x}-1}dx$$
も類題として取り組みましょう。
ガンマ関数を整理して有限和をとる
$\mathfrak{R}s>1$ についてガンマ関数$$\G(s)=\int_0^\infty x^{s-1}e^{-x}dx$$を考えます。複素数の指数があるので一応 $\arg x=0$ と断っておきます。積分変数を $x=(n+a)y$ と置換します。$$\G(s)=(n+a)^s\int_0^\infty y^{s-1}e^{-(n+a)y}dy$$$$\therefore\quad\frac{1}{(n+a)^s}\G(s)=\int_0^\infty x^{s-1}e^{-(n+a)x}dx$$
$n=0$ から $N$ まで和をとりましょう。$$\G(s)\sum_{n=0}^N\frac{1}{(n+a)^s}=\sum_{n=0}^N\int_0^\infty x^{s-1}e^{-(n+a)x}dx$$右辺のシグマとインテグラルを入れ替えます。$$\sum_{n=0}^N\frac{1}{(n+a)^s}=\frac{1}{\G(s)}\int_0^\infty x^{s-1}\left(\sum_{n=0}^N e^{-(n+a)x}\right)dx$$右辺は等比数列の和を計算して$$\sum_{n=0}^N\frac{1}{(n+a)^s}=\frac{1}{\G(s)}\int_0^\infty x^{s-1}\left(\frac{e^{-ax}-e^{-(N+a+1)x}}{1-e^{-x}}\right)dx$$
Nの極限をとる
右辺の被積分関数第2項の $N\to\infty$ の極限が $0$ になることを示します。\begin{eqnarray*}\left|\int_0^\infty \frac{x^{s-1}e^{-(N+a+1)x}}{1-e^{-x}}dx\right|&\le&\int_0^\infty\left| \frac{x^{s-1}e^{-(N+a+1)x}}{1-e^{-x}}\right|dx\\&=&\int_0^\infty\left| \frac{x^{s-1}e^{-(N+a)x}}{e^x-1}\right|dx\\&=&\int_0^\infty\left|x^{s-2}e^{-(N+a)x}\frac{x}{e^x-1}\right|dx\\&\le&\int_0^\infty\left|x^{s-2}e^{-(N+a)x}\right|dx\\&=&\int_0^\infty x^{\sigma-2}e^{-(N+a)x}dx\end{eqnarray*}ここで $\sigma>1$ は $s$ の実部です。$(N+a)x=t$ と置換すれば\begin{eqnarray*}\left|\int_0^\infty \frac{x^{s-1}e^{-(N+a+1)x}}{1-e^{-x}}dx\right|&\le&\frac{1}{(N+a)^{\sigma-1}}\int_0^\infty t^{\sigma-2}e^{-t}dt\\&=&\frac{\G(\sigma-1)}{(N+a)^{\sigma-1}}\\&&\xrightarrow[N\to\infty]{}0\end{eqnarray*}
よって極限ではこの項は消え、$$\displaystyle\lim_{N\to\infty}\sum_{n=0}^N\frac{1}{(n+a)^s}=\frac{1}{\G(s)}\int_0^\infty x^{s-1}\frac{e^{-ax}}{1-e^{-x}}dx$$
$$\therefore\quad\zeta(s,a)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{-ax}}{1-e^{-x}}dx$$
これで目標は達成できました!
同様の方法で$$(1-2^{1-s})\zeta(s)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}}{e^x+1}dx\quad(\mathfrak{R}s>0)$$を示せ($s\neq 1$)。
左辺の $1-2^{1-s}$ はゼータ関数でよくある形です。これは次のように交代級数をいじることで現れます。\begin{eqnarray*}\frac{1}{1^s}-\frac{1}{2^s}+\frac{1}{3^s}-\cdots&=&\left(\frac{1}{1^s}+\frac{1}{2^s}+\frac{1}{3^s}+\cdots\right)-2\left(\frac{1}{2^s}+\frac{1}{4^s}+\frac{1}{6^s}+\cdots\right)\\&=&\zeta(s)-2\cdot2^{-s}\zeta(s)\\&=&(1-2^{1-s})\zeta(s)\end{eqnarray*}
さて $\mathfrak{R}s>1$ についてガンマ関数$$\G(s)=\int_0^\infty x^{s-1}e^{-x}dx$$を考えます。$x=ny$ とおきます。$$\G(s)=n^s\int_0^\infty y^{s-1}e^{-ny}dy$$$(-1)^n$ をかけることで$$-\frac{(-1)^{n-1}}{n^s}=\frac{1}{\G(s)}\int_0^\infty y^{s-1}(-e^{-y})^ndy$$
$n=1$ から $N$ まで和をとりましょう。\begin{eqnarray*}-\sum_{n=1}^N\frac{(-1)^{n-1}}{n^s}&=&\frac{1}{\G(s)}\int_0^\infty y^{s-1}\left(\sum_{n=1}^N(-e^{-y})^n\right)dy\\&=&\frac{-1}{\G(s)}\int_0^\infty y^{s-1}\frac{1-(-e^{-y})^N}{e^y+1}dy\end{eqnarray*}
ここで積分第2項を考えます。$\mathfrak{R}s=\sigma>0$ とします。\begin{eqnarray*}\left|\int_0^\infty \frac{x^{s-1}(-e^{-x})^N}{e^x+1}dx\right|&\le&\int_0^\infty \frac{\left|x^{s-1}\right|e^{-Nx}}{e^x+1}dx\\&\le&\int_0^\infty \left|x^{s-1}\right|e^{-Nx}dx\\&=&\int_0^\infty x^{\sigma-1}e^{-Nx}dx\\&=&\frac{1}{N^\sigma}\int_0^\infty t^{\sigma-1}e^{-t}dt\quad(Nx=t)\\&=&\frac{\G(\sigma)}{N^\sigma}\\&&\xrightarrow[N\to\infty]{}0\end{eqnarray*}
$$\therefore\quad\sum_{n=1}^\infty\frac{(-1)^{n-1}}{n^s}=\frac{1}{\G(s)}\int_0^\infty \frac{x^{s-1}}{e^x+1}dx$$左辺は $(1-2^{1-s})\zeta(s)$ でしたから
$$(1-2^{1-s})\zeta(s)=\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}}{e^x+1}dx$$
$\mathfrak{R}s>1$ とする$$\zeta (s)=\frac{2^s}{(2^s-1)\G(s)}\int_0^\infty\frac{x^{s-1}e^{x}}{e^{2x}-1}dx$$を示せ。
(2)より\begin{eqnarray*}\zeta\left(s,\frac{1}{2}\right)&=&\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{-\frac{x}{2}}}{1-e^{-x}}dx\\&=&\frac{1}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{\frac{x}{2}}}{e^x-1}dx\\&=&\frac{2^s}{\G(s)}\int_0^\infty\frac{y^{s-1}e^{y}}{e^{2y}-1}dy\quad(x=2y)\\&=&\frac{2^s}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{x}}{e^{2x}-1}dx\end{eqnarray*}
一方\begin{eqnarray*}\zeta\left(s,\frac{1}{2}\right)&=&\sum_{n=0}^\infty\frac{1}{(n+\frac{1}{2})^s}\\&=&2^s\sum_{n=0}^\infty\frac{1}{(2n+1)^s}\\&=&2^s\sum_{n:odd}\frac{1}{n^s}\\&=&2^s\left(\sum_{n=1}^\infty\frac{1}{n^s}-\sum_{n=1}^\infty\frac{1}{(2n)^s}\right)\\&=&2^s(\zeta(s)-\frac{1}{2^s}\zeta(s))\\&=&(2^s-1)\zeta(s)\end{eqnarray*}
$$\therefore\quad(2^s-1)\zeta(s)=\frac{2^s}{\G(s)}\int_0^\infty\frac{x^{s-1}e^{x}}{e^{2x}-1}dx$$
フルヴィッツゼータ関数の積分表示を学びました。$a=1$ とすることでリーマンゼータ関数の積分表示も兼ねていることが分かります。次回もフルヴィッツゼータ関数を基本として見ていきます。次回はハンケル積分路を用いた複素積分によってゼータ関数を表現します:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。