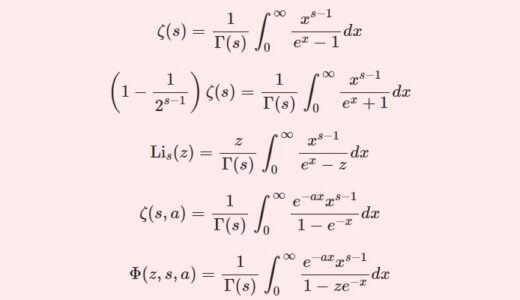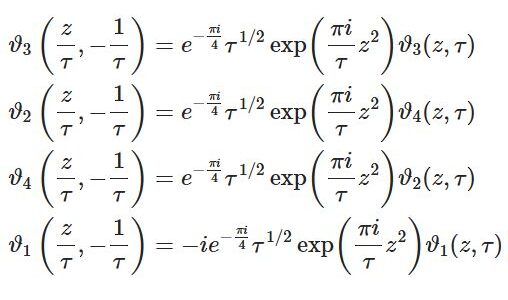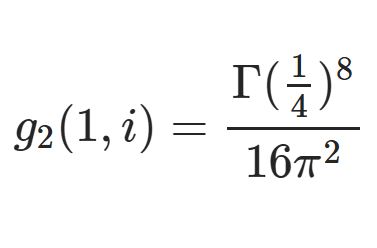\begin{equation}\int_0^\infty\frac{x^m}{\sinh x}dx=m!(2-2^{-m})\zeta(m+1)\quad(m\in\NN)\tag{1}\end{equation}\begin{equation}\int_0^\infty\frac{x^m}{\cosh x}dx=m!\cdot 2\cdot\beta(m+1)\quad(m\in\ZZ_{\ge 0})\tag{2}\end{equation}ただし $\zeta(s)$ は「リーマンのゼータ関数」, $\beta(s)$ は「ディリクレのベータ関数」
今回はこれらの少し難しそうな積分について解説します.参考となる過去記事を貼っておきますが、読まなくても今日の記事は読めます:
4つのゼータ系特殊関数
リーマンのゼータ関数\begin{equation}\zeta(s)=\sum_{n=0}^\infty\frac{1}{n^s}\tag{3}\end{equation}フルヴィッツのゼータ関数\begin{equation}\zeta(s,a)=\sum_{n=0}^\infty\frac{1}{(n+a)^s}\tag{4}\end{equation}ディリクレのベータ関数\begin{equation}\beta(s)=\sum^\infty_{n=0}\frac{(-1)^n}{(2n+1)^s}\tag{5}\end{equation}レルヒの超越関数\begin{equation}\Phi(z,s,a)\equiv \sum_{n=0}^\infty\frac{z^n}{(n+a)^s}\tag{6}\end{equation}
形から分かるようにすべてゼータ系の特殊関数です.リーマンのゼータ関数は $s$ が偶数のときは厳密な値が知られています.ディリクレのベータ関数は,$B(x,y)$ と書かれる知名度の高い「ベータ関数」とは別物です.この関数はゼータとは逆に $s$ が奇数のときの値はよく知られています.
フルヴィッツゼータとレルヒの超越関数は積分表示すると(1)(2)が現れてきます.明らかに(4)は(6)に含まれています.
フルヴィッツゼータ関数の積分表示
ガンマ関数$$\Gamma(s)\equiv\int^\infty_0e^{-x}x^{s-1}dx$$において $x=(n+a)t$ ($n\in\mathbb{Z}^+$)と変換すると$$\Gamma(s)=(n+a)^s\int^\infty_0e^{-(n+a)t}t^{s-1}dt$$よって$$\frac{1}{(n+a)^s}=\frac{1}{\Gamma(s)}\int^\infty_0(e^{-t})^ne^{-at}t^{s-1}dt$$$n$ について非負整数で和をとります.\begin{eqnarray*}\sum^\infty_{n=0}\frac{1}{(n+a)^s}&=& \frac{1}{\Gamma(s)}\int^\infty_0\sum^\infty_{n=0}(e^{-t})^ne^{-at}t^{s-1}dt\\ &=& \frac{1}{\Gamma(s)}\int^\infty_0\frac{e^{-at}t^{s-1}}{1-e^{-t}}dt\end{eqnarray*}これと(4)から次の関係式を得ます.
\begin{equation}\zeta(s,a)=\frac{1}{\Gamma(s)}\int^\infty_0\frac{e^{-ax}x^{s-1}}{1-e^{-x}}dx\tag{7}\end{equation}
レルヒの超越関数の積分表示
同様のことをレルヒの超越関数でやります.実はさきほどのフルヴィッツはこちらの特別な場合なので,やる必要はなかったのですが…
先ほどと同様,ガンマ関数の積分表示において $x=(n+a)t$ ($n\in\mathbb{Z}^+$)と変換すると$$\Gamma(s)=(n+a)^s\int^\infty_0e^{-(n+a)t}t^{s-1}dt$$よって$$\frac{1}{(n+a)^s}=\frac{1}{\Gamma(s)}\int^\infty_0(e^{-t})^ne^{-at}t^{s-1}dt$$$z^n$ を両辺にかけて$$\frac{z^n}{(n+a)^s}=\frac{1}{\Gamma(s)}\int^\infty_0(ze^{-t})^ne^{-at}t^{s-1}dt$$$n$ に関して非負整数で和をとると\begin{eqnarray*}\sum^\infty_{n=0}\frac{z^n}{(n+a)^s}&=& \frac{1}{\Gamma(s)}\int^\infty_0\sum^\infty_{n=0}(ze^{-t})^ne^{-at}t^{s-1}dt\\ &=& \frac{1}{\Gamma(s)}\int^\infty_0\frac{e^{-at}t^{s-1}}{1-ze^{-t}}dt\end{eqnarray*}これと(6)から次の関係式を得ます.
\begin{equation}\Phi(z,s,a)=\frac{1}{\Gamma(s)}\int^\infty_0\frac{e^{-ax}x^{s-1}}{1-ze^{-x}}dx\tag{8}\end{equation}
$m$ を自然数として積分を変形させていくと\begin{eqnarray*}\int_0^\infty\frac{x^m}{\sinh x}dx &=& \int_0^\infty\frac{2x^m}{e^x-e^{-x}}dx \\&=& \int_0^\infty\frac{2x^me^{-x}}{1-e^{-2x}}dx \\&=& \int_0^\infty\frac{(x/2)^me^{-x/2}}{1-e^{-x}}dx \\&=& 2^{-m}\int_0^\infty\frac{x^me^{-\frac{x}{2}}}{1-e^{-x}}dx \\&=& 2^{-m}m!\frac{1}{\Gamma(m+1)}\int_0^\infty\frac{x^me^{-\frac{x}{2}}}{1-e^{-x}}dx \\&=& 2^{-m}m!\,\zeta(m+1,\frac{1}{2})\quad(\because(7))\\ &=& 2^{-m}m! \sum_{n=0}^\infty\frac{1}{(n+\frac{1}{2})^{m+1}}\quad(\because(2))\\ &=& 2\cdot m! \sum_{n=0}^\infty\frac{1}{(2n+1)^{m+1}}\\ &=& 2\cdot m! \sum_{n:\mathrm{odd}}\frac{1}{n^{m+1}}\\&=& 2\cdot m!\left[ \sum_{n=1}^\infty\frac{1}{n^{m+1}}-\sum_{n:\mathrm{even}}\frac{1}{n^{m+1}}\right]\\ &=& 2\cdot m!\left[ \zeta(m+1)-\sum_{n=1}^\infty\frac{1}{(2n)^{m+1}}\right]\\ &=& 2\cdot m!\left[ \zeta(m+1)-2^{-m-1}\zeta(m+1)\right]\\&=&m!(2-2^{-m})\zeta(m+1)\end{eqnarray*}\begin{equation*}\therefore\;\int_0^\infty\frac{x^m}{\sinh x}dx=m!(2-2^{-m})\zeta(m+1)\end{equation*}
よって冒頭の積分(1)を証明できました.これを用いることで\begin{eqnarray*}\int_0^\infty\frac{x}{\sinh x}dx&=&\frac{\pi^2}{4}\\\int_0^\infty\frac{x^2}{\sinh x}dx&=&\frac{7}{2}\zeta(3)\\\int_0^\infty\frac{x^3}{\sinh x}dx&=&\frac{\pi^4}{8}\\\int_0^\infty\frac{x^4}{\sinh x}dx&=&\frac{93}{2}\zeta(5)\\\int_0^\infty\frac{x^5}{\sinh x}dx&=&\frac{\pi^6}{4}\\\int_0^\infty\frac{x^6}{\sinh x}dx&=&\frac{5715}{4}\zeta(7)\\\int_0^\infty\frac{x^7}{\sinh x}dx&=&\frac{17}{16}\pi^8\end{eqnarray*}などと書くことができます.眺めてみると何だか不思議な感じがします.左辺を見ても $\pi$ が出てきたり,ゼータが関わったりするようには思えないですね.奇数ゼータのほうはそもそも無理として,値が分かっているものはマトモに積分で求められるのだろうか?と疑問に思います.つまりフルヴィッツゼータを使わずに高等学校レベルでもやれる式変形とか.
\begin{eqnarray*}\int_0^\infty\frac{x^m}{\cosh x}dx &=& \int_0^\infty\frac{2x^m}{e^x+e^{-x}}dx\\ &=& \int_0^\infty\frac{2x^me^{-x}}{1+e^{-2x}}dx\\ &=& \int_0^\infty\frac{2(x/2)^me^{-\frac{x}{2}}}{1+e^{-x}}\frac{dx}{2}\\ &=& \frac{1}{2^m}\int_0^\infty\frac{e^{-\frac{x}{2}}x^m}{1+e^{-x}}dx\\ &=&\frac{1}{2^m}\Gamma(m+1)\Phi\left(-1,m+1,\frac{1}{2}\right)\quad(\because(8))\\&=& \frac{m!}{2^m}\sum^\infty_{n=0}\frac{(-1)^n}{(n+\frac{1}{2})^{m+1}}\quad(\because(6))\\ &=& \frac{m!}{2^m}\cdot 2^{m+1}\sum^\infty_{n=0}\frac{(-1)^n}{(2n+1)^{m+1}}\\ &=& m!\cdot 2\sum^\infty_{n=0}\frac{(-1)^n}{(2n+1)^{m+1}}\\&=&m!\cdot 2\cdot\beta(m+1)\quad(\because(5))\end{eqnarray*}$$\therefore\quad\int_0^\infty\frac{x^m}{\cosh x}dx=m!\cdot 2\cdot\beta(m+1)$$
よって冒頭の積分(2)を証明できました.
ディリクレベータの値が分かれば,積分値を具体的に書けることになります.$\beta(1)$ はライプニッツ級数ですね.$$\begin{cases}\beta(1)&=&\displaystyle\frac{\pi}{4}\\\beta(2)&=& G\\\beta(3)&=& \displaystyle\frac{\pi^3}{32}\\\beta(2k+1)&=&\displaystyle\frac{(-1)^nE_{2k}\pi^{2k+1}}{4^{k+1}(2k)!}\end{cases}$$$G$ はカタラン定数です.引数が偶数のときのベータの値は分かっていません.奇数のときの値には一般に $E_k$ が用いられていますが,これはオイラー数といって $1/\cosh x$ をテイラー展開して得られる係数です.$$\frac{1}{\cosh x}=\sum^\infty_{n=0}\frac{E_n}{n!}x^n$$例えば $E_0=1$ , $E_1=0$ , $E_2=-1$ , $E_3=0$ , $E_4=5\cdots$ といった具合です.これを使うことで $\beta(2k+1)$ の値を計算できるのです.
\begin{eqnarray*}\int_0^\infty\frac{1}{\cosh x}dx&=&\frac{\pi}{2}\\ \int_0^\infty\frac{x}{\cosh x}dx&=&2G\\ \int_0^\infty\frac{x^2}{\cosh x}dx&=&\frac{\pi^3}{8}\\ \int_0^\infty\frac{x^3}{\cosh x}dx&=&12\beta(4)\\\int_0^\infty\frac{x^4}{\cosh x}dx&=&\frac{5\pi^5}{32}\\ \int_0^\infty\frac{x^5}{\cosh x}dx&=&240\beta(6)\\\int_0^\infty\frac{x^6}{\cosh x}dx&=&\frac{61}{128}\pi^7\end{eqnarray*}
以上,最後に今回得られた積分を並べておきます.
\begin{equation}\int_0^\infty\frac{x^m}{\sinh x}dx=m!(2-2^{-m})\zeta(m+1)\quad(m\in\NN)\tag{1}\end{equation}\begin{equation}\int_0^\infty\frac{x^m}{\cosh x}dx=m!\cdot 2\cdot\beta(m+1)\quad(m\in\ZZ_{\ge 0})\tag{2}\end{equation}
あらたにゼータ関数の基礎シリーズを開講しました!
ディリクレのベータ関数を使った積分:
特殊関数の記事
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。