Integrals and Miscellaneous 1

$$\begin{eqnarray*}\int_{0}^{\infty} (1-x\arctan\frac{1}{x})dx&=&\int_{\epsilon}^{\infty}\left(\frac{1}{x^2}-\frac{\arctan x}{x^3}\right)dx\\&=&\frac{1}{\epsilon}+\left[\frac{\arctan x}{2x^2}\right]_\epsilon^\infty-\frac{1}{2}\int_{\epsilon}^{\infty}\frac{dx}{x^2(1+x^2)}\\&=&\frac{\pi}{4}+\frac{1}{2\epsilon}-\frac{1}{2\epsilon^2}\arctan\epsilon\\&=&\frac{\pi}{4}+\frac{1}{2\epsilon}-\frac{1}{2\epsilon^2} \left(\epsilon+O(\epsilon^3)\right)\\&=&\frac{\pi}{4}\end{eqnarray*}$$

$$\begin{eqnarray*}&&\int_{-\frac{\pi}{2}}^{\frac{\pi}{2}}\frac{1-\cos^2x}{1+\cos^2x}dx\\&=&4\int_0^1\left(\frac{1+t^2}{1+t^4}-\frac{1}{1+t^2}\right)dt\\&=&4\int_0^1\left(\frac{1/2}{t^2-\sqrt{2}t+1}+\frac{1/2}{t^2+\sqrt{2}t+1}\right)-\pi\\&=&2\sqrt{2}\left(\arctan(\sqrt{2}-1)+\arctan(\sqrt{2}+1)\right)-\pi\\&=&\pi(\sqrt{2}-1)\end{eqnarray*}$$

Indefinite integral

$$\begin{eqnarray*}\int\frac{1-\cos^2x}{1+\cos^2x}dx&=&\int\frac{\csc^2x-\cot^2x}{\csc^2+\cot^2x}dx\end{eqnarray*}$$ $$\cot x=y,\csc^2xdx=-dy,\csc^2x=1+y^2$$ $$\begin{eqnarray*}\int\frac{-dy}{(1+2y^2)(1+y^2)}&=&\int\frac{dy}{1+y^2}-\int\frac{2dy}{1+2y^2}\\&=&\arctan y-\sqrt{2}\arctan\sqrt{2}y+C'\\&=&\arctan\cot x-\sqrt{2}\arctan(\sqrt{2}\cot x)+C'\\&=&\frac{\pi}{2}-x-\sqrt{2}\left(\frac{\pi}{2}-\arctan\frac{\tan x}{\sqrt{2}}\right)+C'\\&=&\sqrt{2}\arctan\frac{\tan x}{\sqrt{2}}-x+C\end{eqnarray*}$$

$$\begin{eqnarray*}\int_0^\infty\frac{x^4dx}{4\cosh^2x-1}&=&\int_0^\infty\frac{x^4e^{-2x}dx}{e^{-4x}+e^{-2x}+1}\\&=&\int_0^\infty\frac{x^4(e^{-2x}-e^{-4x})dx}{1-e^{-6x}}\\&=&\int_0^\infty\frac{x^4e^{-2x}dx}{1-e^{-6x}}-\int_0^\infty\frac{x^4e^{-4x}dx}{1-e^{-6x}}\\&=&\frac{1}{6^5}\left[\int_0^\infty\frac{x^4e^{-\frac{1}{3}x}dx}{1-e^{-x}}-\int_0^\infty\frac{x^4e^{-\frac{2}{3}x}dx}{1-e^{-x}}\right]\\&=&\frac{4!}{6^5}\left[\zeta\left(5,\frac{1}{3}\right)-\zeta\left(5,\frac{2}{3}\right)\right]\\&=&\frac{4!}{6^5}\cdot\frac{(6\pi)^5}{4!\cdot2}\frac{2}{\sqrt{3}}\zeta\left(-4,\frac{1}{3}\right)\\&=&-\frac{\pi^5}{5\sqrt{3}}B_5(1/3)\\&=&-\frac{\pi^5}{5\sqrt{3}}\left[-\frac{5}{243}\right]\\&=&\frac{\pi^5}{243\sqrt{3}}\end{eqnarray*}$$

$$\begin{eqnarray*}\int_0^1\frac{\arcsin x}{x}dx&=&\int_0^\frac{\pi}{2}\theta\cot\theta d\t\quad(\sin\t=x)\\&=&\left[\t\log\sin\t\right]_0^\frac{\pi}{2}-\int_0^\frac{\pi}{2}\log\sin\t d\t\\&=&-\int_0^\frac{\pi}{2}\log\sin\t d\t\\&=&-\frac{1}{4}\dd{B}{x}\left(\frac{1}{2},\frac{1}{2}\right)\\&=&-\frac{1}{4}B\left(\frac{1}{2},\frac{1}{2}\right)\left[\psi\left(\frac{1}{2}\right)-\psi(1)\right]\\&=&-\frac{1}{4}\pi(-2\log2)\\&=&\frac{\pi}{2}\log2\end{eqnarray*}$$

Integral representation of the digammma function by Gauss

$$\begin{eqnarray*}I&&=\int_0^1\left(\frac{1}{1-x}+\frac{1}{\log x}\right)dx\\&&=\int_0^\infty\left(\frac{1}{1-e^{-t}}-\frac{1}{t}\right)e^{-t}dt\quad(t=-\log x)\\&&=\displaystyle\lim_{s\to0}\int_0^\infty t^{s}\left(\frac{1}{1-e^{-t}}-\frac{1}{t}\right)e^{-t}dt\\&&=\displaystyle\lim_{s\to0}\int_0^\infty\left(\frac{t^s}{e^t-1}-t^{s-1}e^{-t}\right)dt\\&&=\displaystyle\lim_{s\to0}\left[\G(s+1)\zeta(s+1)-\G(s)\right]\\&&=\displaystyle\lim_{s\to0}\left[\G(s+1)\zeta(s+1)-\frac{\G(s+1)}{s}\right]\\&&=\displaystyle\lim_{s\to0}\left[\zeta(s+1)-\frac{1}{s}\right]\\&&=-\psi(1)=\gamma\end{eqnarray*}$$

$$\begin{eqnarray*}\int_0^\infty&&\sin x\arctan\frac{1}{x}dx\\&&=\left[-\cos x\arctan\frac{1}{x}\right]_0^\infty-\int_0^\infty\frac{\cos x}{1+x^2}dx\\&&=\frac{\pi}{2}-\int_0^\infty\frac{\cos x}{1+x^2}dx\\&&=\frac{\pi}{2}\left(1-\frac{1}{e}\right)\quad(*)\end{eqnarray*}$$

(*) can be evaluated by residues.

$$\begin{eqnarray*}I&&=\int_0^\frac{\pi}{2}\log(1+\tan x)dx\\&&=\int_0^\infty\frac{\log(1+y)}{1+y^2}dy\end{eqnarray*}$$ 積分区間を２つに分ける頻出テクニック $$\begin{eqnarray*}I&&=\int_0^1\frac{\log(1+y)}{1+y^2}dy+\int_1^\infty\frac{\log(1+y)}{1+y^2}dy\\&&=\int_0^1\frac{\log(1+y)}{1+y^2}dy+\int_0^1\frac{\log\frac{x+1}{x}}{1+x^2}dx\quad(x=1/y)\\&&=2\int_0^1\frac{\log(1+x)}{1+x^2}dx-\int_0^1\frac{\log x}{1+x^2}dx\\&&=2\int_0^1\frac{\log(1+x)}{1+x^2}dx+G\quad(*)\\&&=2\int_0^1\frac{\log2-\log(1+t)}{1+t^2}dt+G\quad\left(x=\frac{1-t}{1+t}\right)\\&&=\frac{\pi}{2}\log2-2\int_0^1\frac{\log(1+t)}{1+t^2}dt+G\\&&=\frac{\pi}{2}\log2-(I-G)+G\quad(because\;(*))\\&&=\frac{\pi}{2}\log2+2G=I\end{eqnarray*}$$ $$\therefore\quad I=\frac{\pi}{4}\log2+G$$

About (*):

$$\begin{eqnarray*}\int_0^1\frac{\log x}{1+x^2}dx&&=\int_0^1\log x\sum_{n=0}^\infty(-x^2)^ndx\\&&=-\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}\\&&=-G\end{eqnarray*}$$

$$\begin{eqnarray*}\int_0^1&&\arcsin x\arccos xdx\\&&=\frac{\pi}{2}\int_0^1\arcsin xdx-\int_0^1\arcsin^2xdx\end{eqnarray*}$$

First term of the RHS: $$\begin{eqnarray*}\int_0^1\arcsin xdx&&=\left[x\arcsin x\right]_0^1-\int_0^1\frac{x}{\sqrt{1-x^2}}dx\\&&=\frac{\pi}{2}-1\end{eqnarray*}$$

Second term of the RHS: $$\begin{eqnarray*}\int_0^1\arcsin^2xdx&&=\left[x\arcsin^2x\right]_0^1-2\int_0^1x\arcsin x\frac{dx}{\sqrt{1-x^2}}\\&&=\frac{\pi^2}{4}+2\left[\sqrt{1-x^2}\arcsin x\right]_0^1-2\\&&=\frac{\pi^2}{4}-2\end{eqnarray*}$$

$$\therefore\quad\int_0^1\arcsin x\arccos xdx=2-\frac{\pi}{2}$$

$$\begin{eqnarray*}I&&=\int_0^\frac{\pi}{2}\frac{\arctan\sin x}{\sin x}dx\\&&=\int_0^1\frac{\arctan t dt}{t\sqrt{1-t^2}}\quad(x=\arcsin t)\end{eqnarray*}$$

Define $I(a)=\displaystyle\int_0^1\frac{\arctan at dt}{t\sqrt{1-t^2}}$ , then $I=I(1)$ , $I(0)=0$. $$\begin{eqnarray*}I'(a)&&=\int\frac{dt}{\sqrt{1-t^2}(1+a^2t^2)}\\&&=\int_0^\frac{\pi}{2}\frac{du}{1+a^2\sin^2u}\quad(t=\sin u)\\&&=\int_0^\infty\frac{dy}{y^2+a^2+1}\quad(y=\cot u)\\&&=\frac{\pi}{2}\frac{1}{\sqrt{1+a^2}}\end{eqnarray*}$$ $$\therefore\quad I(a)=\frac{\pi}{2}\log\left(a+\sqrt{1+a^2}\right)$$ $$\therefore\quad I=\frac{\pi}{2}\log(1+\sqrt{2})$$

$$I=\int_0^\infty\frac{x\sin x}{1+x^2}dx=\frac{1}{2}\int_{-\infty}^\infty\frac{x\sin x}{1+x^2}dx$$

$$\oint_C\frac{ze^{iz}}{1+z^2}dz=2\int_0^\infty\frac{xe^{ix}}{1+x^2}dx+\int_\G\frac{ze^{iz}}{1+z^2}dz$$ $C$:semicircle of large radius $R$ which includes a pole $z=i$. $\G$ is the big arc of $C$. $$\oint_C=\left.2\pi i\frac{ze^{iz}}{z+i}\right|_{z=i}=i\frac{\pi}{e}$$

$$\begin{eqnarray*}\left|\int_\G\right|&&\le\int_0^\pi\left|\frac{Re^{i\t}e^{iRe^{i\t}}}{1+R^2e^{2i\t}}ie^{i\t}\right|d\t\\&&\le\int_0^\pi\left|\frac{Re^{-R\sin\t}}{R^2-1}\right|d\t\\&&=\frac{R}{R^2-1}\int_0^\pi e^{-R\sin\t}d\t\\&&=\frac{2R}{R^2-1}\int_0^\frac{\pi}{2} e^{-R\sin\t}d\t\\&&\le\frac{\pi R}{R^2-1}\\&&\longrightarrow 0\quad(as\quad R\to\infty)\end{eqnarray*}$$

Hence, $$\int_0^\infty\frac{x\sin x}{1+x^2}dx=\frac{\pi}{2e}$$

$$I=\int_0^\infty\frac{\cos x^2-\cos x}{x}dx$$

$$\begin{eqnarray*}\int_\epsilon^\infty\left(\frac{1}{1+x}-\cos x\right)\frac{dx}{x}&&=\left[\log\frac{x}{1+x}\right]_\epsilon^\infty+\mathrm{Ci}(\epsilon)\\&&=-\log\epsilon+\gamma+\log\epsilon\\&&=\gamma\end{eqnarray*}$$ Hence, $$\begin{equation}\int_0^\infty\left(\frac{1}{1+x}-\cos x\right)\frac{dx}{x}=\gamma\tag{1}\end{equation}$$

Let $x\to x^2$ , we get $$\begin{equation} \int_0^\infty\left(\frac{1}{1+x^2}-\cos x^2\right)\frac{dx}{x}=\frac{1}{2}\gamma\tag{2}\end{equation}$$ (1)-(2), we obtain $$\frac{\gamma}{2}=\int_0^\infty\frac{x-1}{(1+x)(1+x^2)}dx+I$$

$$\begin{eqnarray*}&&\int_0^\infty\frac{x-1}{(1+x)(1+x^2)}dx\\&&=\int_0^1\frac{x-1}{(1+x)(1+x^2)}dx+\int_1^\infty\frac{x-1}{(1+x)(1+x^2)}dx\\&&=\int_0^1\frac{x-1}{(1+x)(1+x^2)}dx+\int_0^1\frac{\frac{1}{x}-1}{(1+\frac{1}{x})(1+\frac{1}{x^2})}\frac{dx}{x^2}\\&&=\int_0^1\frac{x-1}{(1+x)(1+x^2)}dx-\int_0^1\frac{x-1}{(1+x)(1+x^2)}dx\\&&=0\end{eqnarray*}$$

Therefore, $$I=\frac{\gamma}{2}$$

$$\begin{eqnarray*}I&&=\int_0^\pi\log\left(2\sin\frac{x}{2}\right)\log\left(2\cos\frac{x}{2}\right)dx\\&&=\int_0^\pi\left(\log^22+\log2\log\left(\sin\frac{x}{2}\cos\frac{x}{2}\right)+\left(\log\sin\frac{x}{2}\right)\left(\log\cos\frac{x}{2}\right)\right)\\&&=\log2\int_0^\pi\log\sin xdx+\int_0^\pi\left(\log\sin\frac{x}{2}\right)\left(\log\cos\frac{x}{2}\right)dx\\&&=2\log2\int_0^\frac{\pi}{2}\log\sin xdx+2\int_0^\frac{\pi}{2}\left(\log\sin x\right)\left(\log\cos x\right)dx\end{eqnarray*}$$

These two integrals are evaluated below: $$\begin{eqnarray*}\int_0^\frac{\pi}{2}\log\sin xdx&&=\frac{1}{4}\dd{B}{x}\left(\frac{1}{2},\frac{1}{2}\right)\\&&=\frac{1}{4}B\left(\frac{1}{2},\frac{1}{2}\right)\left(\psi\left(\frac{1}{2}\right)-\psi(1)\right)\\&&=-\frac{\pi}{2}\log2\end{eqnarray*}$$ $$\begin{eqnarray*}&&\int_0^\frac{\pi}{2}\left(\log\sin x\right)\left(\log\cos x\right)dx\\&&=\frac{1}{8}\frac{\partial^2B}{\partial x\partial y}\left(\frac{1}{2},\frac{1}{2}\right)\\&&=\frac{1}{8}B\left(\frac{1}{2},\frac{1}{2}\right)\left[\left(\psi\left(\frac{1}{2}\right)-\psi(1)\right)^2-\psi'(1)\right]\\&&=\frac{\pi}{8}\left[4\log^22-\zeta(2)\right]\\&&=\frac{\pi}{2}\log^22-\frac{\pi^3}{48}\end{eqnarray*}$$ Hence, $$I=-\frac{\pi^3}{24}$$

$$\psi(x)=\sum_{n=-\infty}^\infty e^{-n^2\pi x}\quad(x>0)$$ Consider $$\oint_{C_N}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz$$ $C_N$ is the rectangle whose vertices are $\pm(N+\frac{1}{2})\pm i$.

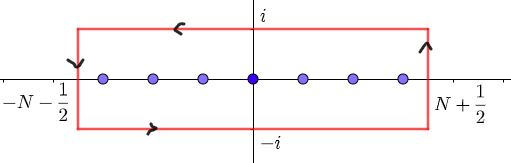
Calculating the residues, let $C_N\to C$ as $N\to\infty$ ,we obtain $$\psi(x)=\oint_{C}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz$$ Separate the contour: $$\psi(x)=\left(\int_{-\infty-i}^{\infty-i}+\int^{\infty+i}_{\infty-i}+\int^{-\infty+i}_{\infty+i}+\int^{-\infty-i}_{-\infty+i}\right)\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz$$ We can easily prove the second and fourth integral tend to zero.

The first integral: $$\begin{eqnarray*}\int_{-\infty-i}^{\infty-i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz&&=\int_{-\infty-i}^{\infty-i}\sum_{n=1}^\infty\exp(-2\pi inz-z^2\pi x)dz\\&&=\sum_{n=1}^\infty e^{-\frac{n^2\pi}{x}}\int_{-\infty-i}^{\infty-i}e^{-\pi x(z+ni/x)^2}dx\\&&=\frac{1}{\sqrt{x}}\sum_{n=1}^\infty e^{-n^2\pi/x}=\frac{1}{\sqrt{x}}\sum_{n=-\infty}^{-1} e^{-n^2\pi/x}\end{eqnarray*}$$ The third integral in the same way: $$\begin{eqnarray*}\int^{-\infty+i}_{\infty+i}\frac{e^{-z^2\pi x}}{e^{2\pi iz}-1}dz=\frac{1}{\sqrt{x}}\sum_{n=0}^{\infty} e^{-n^2\pi/x}\end{eqnarray*}$$ Hence, $$\psi(x)=\frac{1}{\sqrt{x}}\psi\left(\frac{1}{x}\right)$$

Detailed explanation:

2022年3月27日 【ζ8】ゼータ関数・全平面におけるRiemannの積分表示(複素積分・クシー関数)(ゼータ関数の基礎8)

$$I=\int_0^\infty\frac{x^{b-1}}{(1+x^a)^s}dx$$

$$\begin{eqnarray*}B(p,q)&&=\int_0^1t^{p-1}(1-t)^{q-1}dt\\&&=\int_0^\infty\frac{s^{q-1}}{(1+s)^{p+q}}ds\quad(t=\frac{1}{1+s})\\&&=a\int_0^\infty\frac{x^{aq-1}}{(1+x^a)^{p+q}}dx\quad(s=x^a)\end{eqnarray*}$$ Let $p=s-\frac{b}{a}$ , $q=\frac{b}{a}$ then $$I=\frac{1}{a}B\left(s-\frac{b}{a},\frac{b}{a}\right)$$ Hence, $$I=\frac{\G(s-\frac{b}{a})\G(\frac{b}{a})}{a\G(s)}$$

$$\begin{eqnarray*}&&\cos(\sin x)-\sin(\cos x)\\&&=-2\sin\left(\frac{1}{\sqrt{2}}\sin\left(x+\frac{\pi}{4}\right)-\frac{\pi}{4}\right)\cos\left(\frac{1}{\sqrt{2}}\sin\left(x-\frac{\pi}{4}\right)-\frac{\pi}{4}\right)\end{eqnarray*}$$

$$-\frac{\pi}{2}<-\frac{1}{\sqrt{2}}-\frac{\pi}{4}\le\frac{1}{\sqrt{2}}\sin\left(x\pm\frac{\pi}{4}\right)-\frac{\pi}{4}\le\frac{1}{\sqrt{2}}-\frac{\pi}{4}<0$$ Therefore, $$\sin\left(\frac{1}{\sqrt{2}}\sin\left(x+\frac{\pi}{4}\right)-\frac{\pi}{4}\right)<0$$ $$\cos\left(\frac{1}{\sqrt{2}}\sin\left(x-\frac{\pi}{4}\right)-\frac{\pi}{4}\right)>0$$ Hence, $$\cos(\sin x)>\sin(\cos x)$$

$$\int_0^\infty\frac{\cos x-e^{-x}}{x}dx=0$$

Proof is here:

Excercise of Contour Integral (Combination of Real and Imaginary Axis)

$$\begin{eqnarray*}I&&=\int_0^\infty(\sqrt{1+x^4}-x^2)dx\\&&=\int_0^\infty\left(\frac{1}{\sqrt{1+x^4}}+\frac{x^4}{\sqrt{1+x^4}}-x^2\right)dx\\&&=\frac{2}{3}\int_0^\infty\frac{dx}{\sqrt{1+x^4}}-\left[\frac{x^3-x\sqrt{1+x^4}}{3}\right]_0^\infty\\&&=\frac{2}{3}\int_0^\infty\frac{dx}{\sqrt{1+x^4}}\\&&=\frac{1}{6}\int_0^\infty\frac{t^{-\frac{3}{4}}}{(1+t)^\frac{1}{2}}dt\quad(t=x^4)\\&&=\frac{1}{6}B\left(\frac{1}{4},\frac{1}{4}\right)\\&&=\frac{\G^2(\frac{1}{4})}{6\sqrt{\pi}}\end{eqnarray*}$$