もくじ
関数 $f(x)$ が $x=a$ で連続であるとはこういうことです。
任意の $\epsilon>0$ に対してある $\delta>0$ が存在し$$|x-a|<\delta \Rightarrow |f(x)-f(a)|<\epsilon$$とできる。
どんなに小さな $\epsilon$ に対しても、$x$ が $a$ に十分近ければ $|f(x)-f(a)|<\epsilon$ とできますよというわけです。
例えば $|f(x)-f(a)|>0.1$ だとこの関数は $x=a$ で段差ができてしまいます。連続であるには $|f(x)-f(a)|$ がどんな $\epsilon$ よりも小さく抑えられなければならず、その際 $\epsilon$ に応じた小さな数 $\delta$ によって $x$ を $a$ にどれだけ近づければいいのかが示されています。よって $\delta$ は $\epsilon$ や $a$ を用いてあらわされます。
$x\in\mathbb{R}$ で定義される $f(x)=x^2$ は $x=1$ において連続.
$\delta$ をうまく見つけられるかがカギとなります。$$|f(x)-f(1)|=|x^2-1|=|x-1+2||x-1|\le(|x-1|+2)|x-1|$$$|x-1|<\delta$とすると$$|f(x)-f(1)|<\delta^2+2\delta$$よって $\delta^2+2\delta=\epsilon$ となるように $\delta$ をとればよく$$\delta=\sqrt{\epsilon+1}-1$$が見つかります。この $\delta$ は確かに正であり、$\epsilon$ とともにどんどん小さくなっていく数になっていますよね。
さて、この $\delta$ を使って連続性を示しましょう。
任意の $\epsilon>0$ に対して $\delta=\sqrt{\epsilon+1}-1$ ととると、$|x-1|<\delta$ ならば$$|f(x)-f(1)|=|x-1+2||x-1|\le(|x-1|+2)|x-1|<\delta^2+2\delta=\epsilon$$よって連続性が示されました。
$x>0$ で定義される $f(x)=1/x$ は $x=1$ において連続である.
$\delta$ の見つけ方ですが、$|x-1|<\delta$ より $1-\delta<x$ であることに注意し$$\left|\frac{1}{x}-\frac{1}{1}\right|=\frac{|x-1|}{x}<\frac{\delta}{x}<\frac{\delta}{1-\delta}$$この最右辺を $\epsilon$ としてみると $\delta=\displaystyle\frac{\epsilon}{1+\epsilon}$ となるので、この $\delta$ で連続性を示してやれそうです。
実際にやってみます。
任意の $\epsilon>0$ に対して $\delta=\displaystyle\frac{\epsilon}{1+\epsilon}$と定めると$$\left|\frac{1}{x}-\frac{1}{1}\right|=\frac{|x-1|}{x}<\frac{\delta}{x}<\frac{\delta}{1-\delta}=\epsilon$$よって連続性が示されました。
「連続でない」は連続であることの否定をとればよいです。
ある $\epsilon>0$ が存在して、任意の $\delta>0$ に対し$$|x-a|<\delta \;かつ\; |f(x)-f(a)|\ge\epsilon$$となる $x$ が存在する。
$x$ を $a$ にいくら近づけても $f(x)$ と $f(a)$ の差がある値以下にならないということです.否定の取り方は
などを参考にしてください。
イプシロン・デルタ論法のイメージをつかむにはいろいろな角度から例題を見ていくことが大切です。その「角度」の1つが連続性の否定です。否定を学ぶことで連続性のイメージがより理解できます。
$$f(x)=\begin{cases}0\quad(x=0)\\\sin\dfrac{1}{x}\quad(\mathrm{else})\end{cases}$$は $x=0$ で連続でない.
$0$ 付近で激しく振動する関数です。

これが $x=0$ で不連続であることのイメージをつかみましょう。たとえば $x_n=\dfrac{1}{2n\pi}$ として整数 $n$ を大きくしていくと $x_n\to0$ で $\sin\dfrac{1}{x_n}\to 0$ となります。しかし $x_n=\dfrac{1}{2n\pi+\frac{\pi}{2}}$ として同様に考えると $x_n\to0$ で $\sin\dfrac{1}{x_n}\to 1$ となります。よって $x\to0$ の近づけ方によって多様な極限値が得られてしまうので不連続であろうと考えられます。実際、以下のような証明ができます。
$\epsilon=1$ とする。任意の $\delta>0$ に対して$$\left(2N+\frac{1}{2}\right)\pi\delta>1$$なる自然数 $N$ をとって$$x=\frac{1}{\pi(2N+\frac{1}{2})}$$を満たす $x$ を考える。すると $|x|<\delta$ であるが$$\left|f(x)-f(0)\right|=\left|\sin\pi\left(2N+\frac{1}{2}\right)\right|=1\ge\epsilon$$よって不連続である。
上記2つの例題では $x=1$ としましたが、ほかの $x$ についても似たような議論で連続性が示されます。$x=a$ と任意に固定して $a$ と $\epsilon$ に依存する $\delta$ を発見することで、関数全体の連続性を示すことができます。
$x\in\mathbb{R}$ で定義される $f(x)=x^2$ は任意の点 $x=a$ において連続である.
任意の $\epsilon>0$ に対して $\delta=\sqrt{\epsilon+|a|^2}-|a|$ とすると$$\delta^2+2|a|\delta=\epsilon$$ここで
$$|f(x)-f(a)|=|x-a||x+a|=|x-a||x-a+2a|$$最右辺に三角不等式を用いて$$|f(x)-f(a)|\le |x-a|(|x-a|+2|a|)<\delta^2+2|a|\delta=\epsilon$$でOKです。
例題1をもう1度見てみます。
$x\in\mathbb{R}$ で定義される $f(x)=x^2$ は $x=1$ において連続.
先ほどの解答では $\delta=\sqrt{\epsilon+1}-1$ ととりました。これははじめて連続性の証明をするときには最も素直で分かりやすい方法だと思います。しかし $\epsilon-\delta$ 論法による連続性の証明はつまるところ、どう $\delta$ を取るかというテクニックが必要であり、ノウハウをいろいろ知っておかなければならないと私自身も痛感しています。そこで、もちろん上記のように $\delta$ をとってもいいのですが、別解も見てみようと思います。
$\delta \le 1$ のときは $|x-1|<1$ より $-1<x-1<1$ ですので$$|x+1|<3$$が成立します。よって $\epsilon\le 3$ のときは $\delta=\displaystyle\frac{\epsilon}{3}\le 1$ ととると $|x-1|<\delta$ なら$$|x^2-1^2|=|x+1||x-1|<3\cdot\frac{\epsilon}{3}=\epsilon$$でOKです。また $\epsilon> 3$ のときは $\delta=1$ とれば $|x+1|<3$ が成立します。すると$$|x^2-1^2|=|x+1||x-1|<3\delta=3<\epsilon$$でこちらもOKです。
以上から $\delta$ の取り方は$$\delta=\min\left\{\frac{\epsilon}{3},1\right\}$$となります。今回の証明では $|x+1|<3$ を使うのがカギとなっています。しかしこれは $\delta \le 1$ であることが前提ですので $\epsilon$ の値によって $\delta$ が大きくなりすぎないように上限(ここでは1)を式に取り入れたわけです。
また $\delta=\min\left\{\displaystyle\frac{\epsilon}{3},1\right\}$ という取り方は次の式変形でも有効です。$$|f(x)-f(1)|=|x-1+2||x-1|\le(|x-1|+2)|x-1|<\delta^2+2\delta$$最右辺は $\epsilon\le 3$ すなわち $\delta \le 1$ で $\delta^2+2\delta<3\delta=\epsilon$ となりますし、 $\epsilon>3$ では $\delta=1$ ですから $\delta^2+2\delta=3<\epsilon$ とできます。
このようなテクニックを使って例題3に再度取り組んでみます。
$x\in\mathbb{R}$ で定義される $f(x)=x^2$ は任意の点 $x=a$ において連続である.
$\delta \le 1$ のときは $|x-a|<1$ より $-1<x-a<1$ ですので$$2a-1<x+a<2a+1\Rightarrow |x+a|<\max\left\{|2a-1|,|2a+1|\right\}$$が成立します。この $\max\left\{|2a-1|,|2a+1|\right\}$ が先ほどは $3$ だったわけですから、マネて$$\delta=\min\left\{\frac{\epsilon}{\max\left\{|2a-1|,|2a+1|\right\}},1\right\}$$ととってみます。ごちゃっとしてますが、$a$ はただの定数ですから $\max\left\{|2a-1|,|2a+1|\right\}$ だってただの数です!$\min$ の候補に $1$ が入っていることにより $\delta\le 1$ が保証されているので常に $|x+a|<\max\left\{|2a-1|,|2a+1|\right\}$ です。
これにより $\epsilon\le \max\left\{|2a-1|,|2a+1|\right\}$ のときは $\delta=\displaystyle\frac{\epsilon}{\max\left\{|2a-1|,|2a+1|\right\}}\le1 $ ですので\begin{eqnarray*}|x^2-a^2|&=&|x+a||x-a|\\&<&\max\left\{|2a-1|,|2a+1|\right\}\cdot\delta\\&=&\max\left\{|2a-1|,|2a+1|\right\}\cdot\frac{\epsilon}{\max\left\{|2a-1|,|2a+1|\right\}}\\&=&\epsilon\end{eqnarray*}
また $\epsilon> \max\left\{|2a-1|,|2a+1|\right\}$ のときは $\delta=1$ になりますので \begin{eqnarray*}|x^2-a^2|&=&|x+a||x-a|\\&<&\max\left\{|2a-1|,|2a+1|\right\}\delta\\&=&\max\left\{|2a-1|,|2a+1|\right\}\\&<&\epsilon\end{eqnarray*}よって任意の $\epsilon$ に対して証明できました。
$x\in\mathbb{R}$ で定義される $f(x)=x^2+3x$ は $x=a$ において連続である.
$\delta \le 1$ のときは $|x-a|<1$ より $-1<x-a<1$ ですので$$2a+2<x+a+3<2a+4\Rightarrow |x+a+3|<\max\left\{|2a+2|,|2a+4|\right\}$$が成立します。
$$\delta=\min\left\{\frac{\epsilon}{\max\left\{|2a+2|,|2a+4|\right\}},1\right\}$$ととれば $\delta \le 1$ は保証されており、先ほどの議論から $|x+a+3|<\max\left\{|2a+2|,|2a+4|\right\}$ が成り立っています。式変形して$$\delta\cdot\max\left\{|2a+2|,|2a+4|\right\}=\min\left\{\epsilon,\max\left\{|2a+2|,|2a+4|\right\}\right\}$$であることに注意すると\begin{eqnarray*}|x^2+3x-a^2-3a|&=&|x-a||x+a+3|\\&<&\delta\cdot\max\left\{|2a+2|,|2a+4|\right\}\\&=&\min\left\{\epsilon,\max\left\{|2a+2|,|2a+4|\right\}\right\}\le\epsilon\end{eqnarray*}先ほどの説明では $\epsilon$ を場合分けして書いてましたが、こちらように書いた方がスッキリしますね。
$x\in\mathbb{R}$ で定義されるディリクレの関数\begin{equation}f(x)=\begin{cases}1\quad (x\in\mathbb{Q})\\0\quad (x\notin\mathbb{Q})\end{cases}\tag{1}\end{equation}はあらゆる点で不連続である.
$x$ が有理数のときの値は $1$ で,無理数のときは $0$ だというのです.この少し変な関数はすべての点で不連続であることが知られていますので, $\epsilon-\delta$ の練習になりそうだと思って取り上げました.
ディリクレの関数が $x=a$ で連続かどうかを考えます.$a$ が有理数の場合と無理数の場合で分けて考えます.
[ I ] $a$ が有理数の場合
式(1)より $f(a)=1$ です.$x$ を $a$ にいくら近づけても $x$ を無理数にとれることを示せば $f(x)=0$ となって $|f(x)-f(a)|$ は1より小さくなれないことが示せます.
$\epsilon=1$ とします.任意の $\delta>0$ に対して $N>\displaystyle\frac{\sqrt{2}}{\delta}$ なる自然数 $N$ を定め$$x=a+\frac{\sqrt{2}}{N}\quad\notin\mathbb{Q}$$なる $x$ を考えます. $x$ はその定め方から明らかに無理数なので $f(x)=0$ です.また $|x-a|=\displaystyle\frac{\sqrt{2}}{N}<\delta$ となります.ゆえに$$|x-a|<\delta\; かつ\; |f(x)-f(a)|=1\ge\epsilon$$ よって $x=a$ で不連続です.
[ II ] $a$ が無理数の場合
式(1)より $f(a)=0$ です.
$\epsilon=1$ とします.任意の $\delta>0$ に対して $p\delta>1$ なる自然数 $p$ をとると$$p(a+\delta)-p(a-\delta)=2p\delta>2$$よって $p(a+\delta)$ と $p(a-\delta)$ の間には整数 $q$ が存在して\begin{eqnarray*}&&p(a-\delta)<q<p(a+\delta)\\&\Leftrightarrow& a-\delta<\frac{q}{p}<a+\delta\\&\Leftrightarrow&\left|\frac{q}{p}-a\right|<\delta\end{eqnarray*}つまりどのような小さい $\delta$ をとっても $a$ の近傍(半径 $\delta$ )に有理数がありますよということです.
よって $x=\displaystyle\frac{q}{p}$ とすれば $x$ は有理数なので $f(x)=1$ となり$$|x-a|<\delta\; かつ\; |f(x)-f(a)|=1\ge\epsilon$$従って $x=a$ で不連続です.
以上により,ディリクレの関数はすべての点で不連続であることが確認できました!「どんな有理数にも限りなく近いところに無理数がある」,あるいは「どんな無理数にも限りなく近いところに有理数がある」というのは直感的にも分かるのですが,以上のように論証ができるのです.面白いですね.
\begin{equation}f(x)=\begin{cases}\displaystyle\frac{1}{q}\quad (x=\displaystyle\frac{p}{q}\in\mathbb{Q},q\in\mathbb{N},p\in\mathbb{Z},既約)\\[1em] 0\quad(x\notin\mathbb{Q})\end{cases}\tag{2}\end{equation}
$x$ が有理数のときは $x$ を既約分数として表したときの分子を $1$ に置き換えた値をとり,無理数のときは $0$ です.この関数はすべての有理数点で不連続,すべての無理数点で連続である奇妙な関数ですが,$\epsilon-\delta$ の練習になりそうだと思って取り上げました.
この名前はドイツの数学者カール・ヨハネス・トマエにちなんでいますが,ポップコーン関数とよばれることもあります.任意の実数 $x$ に対して定義され,$f(x)$ の値は必ず $[0,1]$ におさまるので有界です.
トマエ関数は周期性をもちます.任意の自然数を $n$ とすると,$x$ が無理数のときは $x+n$ も無理数なので $f(x+n)=f(x)=0$ です.$x$ が(1)で示された既約の有理数 $\dfrac{p}{q}$ だとするとユークリッドの互除法により$$\mathrm{gcd}(p+nq,q)=\mathrm{gcd}(p,q)=1$$従って $p+nq$ と $q$ は既約であるので(1)より $$f(x+n)=f\left(\frac{p+nq}{q}\right)=\frac{1}{q}=f(x)$$よって常に $f(x+n)=f(x)$.
つまりトマエ関数は周期 $1$ なので今後 $x\in [0,1]$ を見れば十分です.グラフはこんな感じ.

比較してみると,トマエ関数はディリクレの関数を修正したようなものだと分かります.しかし連続性に関してはディリクレの関数と異なります.
トマエ関数が $x=a$ で連続かどうかを考えます.$a$ が有理数の場合と無理数の場合で分けて考えます.
[ I ] $a$ が有理数 $\displaystyle\frac{p}{q}$ の場合
$f(a)=1/q$ です.$a$ のいかなる近傍にも無理数が含まれ,$|f(x)-f(a)|$ が $1/q$ 未満に押さえられないと予想できます.この「$a$ にめちゃくちゃ近い無理数」を1つでも明記できればいいですね.
ではやってみます.$\epsilon=1/q$ とします.任意の $\delta>0$ に対して $N>\displaystyle\frac{\sqrt{2}}{\delta}$ なる自然数 $N$ をとり$$x=a+\frac{\sqrt{2}}{N}$$と定めます.この $x$ は無理数ですので $f(x)=0$ です.よって$$|x-a|=\frac{\sqrt{2}}{N}<\delta \;かつ\; |f(x)-f(a)|=\frac{1}{q}\ge\epsilon$$これは不連続ということです.よってあらゆる有理数点での不連続性が示されました。
[ II ] $a$ が無理数の場合
$f(a)=0$ です.$x$ も無理数であれば $|f(x)-f(a)|=0$ となるのでこれ以上論じる必要はありません.
問題は $x$ が有理数の場合です.$\delta$ をうまくとって連続性を示せるでしょうか.簡単のため,区間 $(0,1)$ に絞って考えてみます.
$a$ の周りには有理数点がたくさんあります.しかし $a$ は無理数ですから,それらの有理数と等しくはありません.ですので $\delta$ を十分に小さくとれば $a$ の $\delta$ 近傍からそれらの有理数を排除できます.しかしすべての有理数点を排除するわけではありません(無限回の手続きが必要になってしまうので).分母の小さい有理数点から順に排除していくと,$a$ の近傍に残るのは十分に大きい分母の有理数点であり,$f(x)=1/q$ ですから $f(x)$ は $0$ に近くなります.すると $|f(x)-f(a)|=1/q$ を $\epsilon$ 未満に押さえられるのではないか,と考えるのです.
実際にやっていきましょう.
任意の $\epsilon>0$ に対して $N\epsilon>1$ なる自然数 $N$ をとると $1/N<\epsilon$ が成り立ちます.ここで
・$\delta_2=\left|a-\displaystyle\frac{1}{2}\right|$ ととると $|x-a|<\delta_2$ なる $x$ は $1/2$ を取りえません。よって$1/2$は排除できました.
・$\delta_3=\min\left\{\left|a-\displaystyle\frac{1}{3}\right|,\left|a-\displaystyle\frac{2}{3}\right|\right\}$ ととると $|x-a|<\delta_3$ なる $x$ は $1/3$ , $2/3$ を取りえません.よって$1/3$と$2/3$は排除できました.
以下くりかえし,最後に
・$\delta_N=\min\left\{\left|a-\displaystyle\frac{1}{N}\right|,\cdots,\left|a-\displaystyle\frac{N-1}{N}\right|\right\}$ ととると $|x-a|<\delta_N$ なる $x$ は $1/N$ , $2/N$ ,..., $(N-1)/N$ を取りえません.
ゆえに $\delta=\min\{\delta_2,\delta_3,\cdots,\delta_N\}$ ととれば $|x-a|<\delta$ を満たす有理数 $x$ は分母が $N$ より大きいものに限られます.従って$$|x-a|<\delta\Longrightarrow |f(x)-f(a)|=|f(x)|<\frac{1}{N}<\epsilon$$これであらゆる無理数点での連続性が示されました.
以上①②よりトマエ関数はあらゆる有理数で不連続,あらゆる無理数で連続となります.
$x\in\RR$ で次の関数を定義する.$$f(x):=\begin{cases}x\quad &(x\in\QQ)\\2-x\quad &(x\notin\QQ)\end{cases}$$$f(x)$ は $x=1$ で連続であり、$x\neq1$ で不連続であることを示せ。
(A) $x=1$ での連続性を考える。$\delta=\epsilon$ ととれば $x$ が有理数か無理数かを問わず$$|f(x)-f(1)|=|x-1|<\delta=\epsilon$$よって連続である。
(B) $a\neq 1$ として $x=a$ での連続性を考える。
(i) $a\in\QQ$ のとき任意の $\delta>0$ に対して$$N>\max\left(\frac{\sqrt{2}}{\d},\: \frac{\sqrt{2}}{|1-a|}\right)$$なる $N\in\NN$ をとり、$x=a+\frac{\sqrt{2}}{N}\notin\QQ$ ととると $|x-a|<\d$ を満たす。しかし$$|f(x)-f(a)|\ge 2|1-a|-\frac{\sqrt{2}}{N}\ge |1-a|$$となって不連続。
(ii) $a\notin\QQ$ のとき、ディリクレ関数のときと同様に、任意の $\d>0$ に対して $|\frac{q}{p}-a|<\d$ なる $p\in\NN$ , $q\in\ZZ$ がとれる。$\d$ は任意であったので同時に $|\frac{q}{p}-a|<|1-a|$ を満たすように $p,q$ をとれる。$x=\frac{q}{p}$ とすると $|x-a|<\d$ かつ$$|f(x)-f(a)|=|x-2+a|\ge 2|1-a|-|x-a|\ge |1-a|$$となって不連続。
このように一般には $\delta$ は $a$ によるのですが、$\delta$ が $a$ に依存しない場合はより強い条件である「一様連続」といわれます。次回はその記事を書きます。
書きました↓
こちらを参照ください。
 【ε論法】連続関数の和も積も合成も連続関数
【ε論法】連続関数の和も積も合成も連続関数
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。

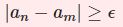
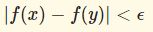
いつも楽しく見せていただいております.
トマエ関数の節のタイトルですが,
「すべての有理数点で不連続」
が正しいかと思われます(本文にはそのように記載されていました).
念のためご連絡させていただきました.
ご覧いただきありがとうございます。ご指摘の箇所を訂正しました。どうもありがとうございました。