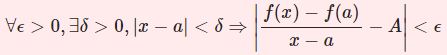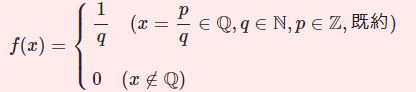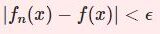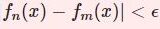一様収束しないことをイプシロン論法で証明する方法を解説します。一様収束の否定をどう表現するか、どのように実践するかを見た後、ただの収束よりも一様収束がうれしいのはなぜかも説明します。
任意の $\epsilon>0$ に対してある自然数 $N$ が存在し$$n\ge N \Rightarrow |f_n(x)-f(x)|<\epsilon$$とできる。
関数列の収束や一様収束の詳しい解説・例題は過去記事を参照ください。
【ε論法】関数列の各点収束と一様収束
今回は「一様収束しない」つまり否定の証明について扱います。関数列 $\{f_n(x)\}$ の一様収束の否定は以下のようになります。
ある $\epsilon>0$ が与えられたとき、任意の自然数 $N$ に対して以下が同時に成り立つ $n$ が存在する。
(1) $n\ge N$
(2) ある $x$ で $|f_n(x)-f(x)|\ge\epsilon$
一様収束は「任意の $\epsilon$ に対して、ホニャララ」という構成ですから、その否定は「ある $\epsilon$ が存在して、ホニャララでない」となります。すべてについて成り立つことの否定は「１つでも成り立たないものがある」ですから。
そのホニャララの内容は「ある $N$ が存在して、ムニャムニャ」ですから、否定バージョンは"そんな $N$ は１つもない！"ということなので「任意の $N$ についてムニャムニャではない」となります。
ここまでで「ある $\epsilon$ が存在して、任意の $N$ についてムニャムニャではない」という形ができます。
で、ムニャムニャとは $n\ge N \Rightarrow |f_n(x)-f(x)|<\epsilon$ のことですが、これは「 $n\ge N$ を満たす すべての $n$ はあらゆる $x$ で$|f_n(x)-f(x)|<\epsilon$ を満たす」という意味ですから、その否定は「 $n\ge N$ を満たしていても、ある $x$ に対しては $|f_n(x)-f(x)|\ge\epsilon$ となってしまう $n$ が存在するよ」です。つまり任意の $N$ で下から抑えられる $n$ はいくらでも大きくとれるのに、$f_n(x)$ と $f(x)$ の差は大きいままだということです。
$x\in[0,1]$ で定義される関数列 $f_n(x)=x^n$ は $$f(x)=\begin{cases} 0\quad (0\le x<1)\\1\quad(x=1)\end{cases} $$ へ収束するが、一様収束しない。
（各点）収束することの証明は過去記事を参照ください。
【ε論法】関数列の各点収束と一様収束
この関数列は $f(x)$ に収束はするものの、一様収束ではありません。
$\epsilon= 1/2$ とします。任意の $N$ に対して $n\ge N$ なる自然数 $n$ をとり、$x=2^{-1/n}$ なる点を考えます。このとき $x\neq 1$ ですので $f(x)=0$ であることに注意します。このとき$$|f_n(x)-f(x)|=|x^n-0|=1/2\ge\epsilon$$つまりどんな自然数 $N$ に対してもそれ以上の $n$ を適当に取れば（というかいくらにとっても）$x=2^{-1/n}$ なる点 $x$ が存在して $|f_n(x)-f(x)|\ge\epsilon$ となってしまうので、一様収束しないということです。
$x=2^{-1/n}$ という点を思いつくのがミソになっています。また、こういうのは絶対値の評価の最右辺に正の定数項がでるような $x,n$ を探すことでうまくいったりします。収束する関数の形をみると $x=1$ あたりがあきらかに怪しいので、$x\to1-0$ となるような $x$ を考えるといいです。
$x\in[0,1]$ で定義される $f_n(x)=nxe^{-nx^2}$ は $f(x)=0$ へ収束するが、これは一様収束でない。
単純に収束することについては解説を省略します。$\epsilon$ 論法で各点収束することを示してもよし、面倒なら高等学校でやったような極限計算で示してもいいでしょう。
$\epsilon=1/3$ とします。任意の自然数 $N$ について、ある $n\ge N$ に対して $x=n^{-1/2} (\in[0,1]) $なる点を考えると$$|f_n(x)-f(x)|=nn^{-1/2}e^{-1}=\frac{\sqrt{n}}{e}\ge\frac{1}{e}>\frac{1}{3}=\epsilon$$$n$ をどれだけ大きくしても点 $x=n^{-1/2}$ において $f_n(x)$と$f(x)$ の差を$1/3$以下にできません。よって一様収束ではありません。
指数部分を定数にすればよさそうなので $x=n^{-1/2}$ ととってみましたが、うまくいきました。関数の形からして $x=0$ 付近が怪しいなぁと思ったのもあります。
一様収束する関数列に関しては次の２つの重要な定理があります。
・連続関数列の収束先も連続関数
・関数列を積分する場合、積分と極限を入れ替え可能
ところが一様収束しない場合は上記が成り立つとは限りません。
先ほどの例題でみた関数列$$x\in[0,1]\;,\; f_n(x)=nxe^{-nx^2}\xrightarrow[n\to\infty]{} f(x)=0$$の積分について見ていきます。$\displaystyle\lim_{n\to\infty}f_n(x)=f(x)=0$ であることに留意します。まず関数列の積分を先にやる場合$$\displaystyle\lim_{n\to\infty}\int^1_0f_n(x)dx=\displaystyle\lim_{n\to\infty}\frac{1-e^{-n}}{2}=\frac{1}{2}$$一方、関数列の極限を先に取る場合$$\int^1_0\displaystyle\lim_{n\to\infty}f_n(x)dx=\int^1_00dx=0$$ということは$$\displaystyle\lim_{n\to\infty}\int^1_0f_n(x)dx\neq\int^1_0\displaystyle\lim_{n\to\infty}f_n(x)dx$$であり、極限と積分の順序を交換できないことになります。なのでフレキシブルに計算ができないという不安があります。一様収束だと順序交換が保障されているので、やはり一様収束はうれしいのです。
ε論法シリーズ
Please support me!
記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。
