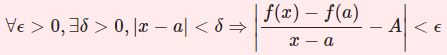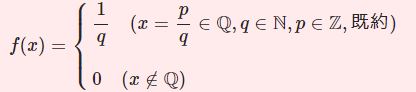トマエ関数とは以下で定義されるものです.
\begin{equation}f(x)=\begin{cases}\displaystyle\frac{1}{q}\quad (x=\displaystyle\frac{p}{q}\in\mathbb{Q},q\in\mathbb{N},p\in\mathbb{Z},既約)\\[1em] 0\quad(x\notin\mathbb{Q})\end{cases}\tag{1}\end{equation}
$x$ が有理数のときは $x$ を既約分数として表したときの分子を $1$ に置き換えた値をとり,無理数のときは $0$ です.この関数はすべての有理数点で不連続,すべての無理数点で連続である奇妙な関数ですが,$\epsilon-\delta$ の練習になりそうだと思って取り上げました.
この名前はドイツの数学者カール・ヨハネス・トマエにちなんでいますが,ポップコーン関数とよばれることもあります.任意の実数 $x$ に対して定義され,$f(x)$ の値は必ず $[0,1]$ におさまるので有界です.
トマエ関数は周期性をもちます.任意の自然数を $n$ とすると,$x$ が無理数のときは $x+n$ も無理数なので $f(x+n)=f(x)=0$ です.$x$ が(1)で示された既約の有理数 $\dfrac{p}{q}$ だとするとユークリッドの互除法により$$\mathrm{gcd}(p+nq,q)=\mathrm{gcd}(p,q)=1$$従って $p+nq$ と $q$ は既約であるので(1)より $$f(x+n)=f\left(\frac{p+nq}{q}\right)=\frac{1}{q}=f(x)$$よって常に $f(x+n)=f(x)$.
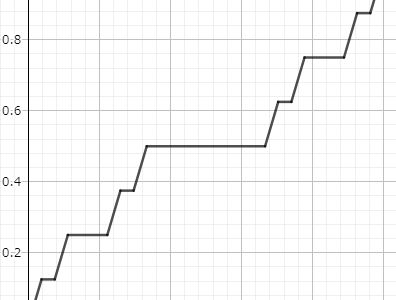
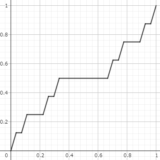
つまりトマエ関数は周期 $1$ なので今後 $x\in [0,1]$ を見れば十分です.グラフはこんな感じ.

関数 $f(x)$ が $x=a$ で連続であるとは
任意の $\epsilon>0$ に対してある $\delta>0$ が存在し$$|x-a|<\delta \Longrightarrow |f(x)-f(a)|<\epsilon$$とできる.
またその否定「関数 $f(x)$ が $x=a$ で連続でない」とは
ある $\epsilon>0$ が与えられたとき,任意の $\delta>0$ について$$|x-a|<\delta\;かつ\; |f(x)-f(a)|\ge\epsilon$$なる $x$ が存在する.
$x$ を $a$ にいくら近づけても $f(x)$ と $f(a)$ の差がある値以下にならないということです.
このあたりの話は以下の記事を参考にしてください.
トマエ関数が $x=a$ で連続かどうかを考えます.$a$ が有理数の場合と無理数の場合で分けて考えます.
① $a$ が有理数 $\displaystyle\frac{p}{q}$ の場合
$f(a)=1/q$ です.$a$ のいかなる近傍にも無理数が含まれ,$|f(x)-f(a)|$ が $1/q$ 未満に押さえられないと予想できます.この「$a$ にめちゃくちゃ近い無理数」を1つでも明記できればいいですね.
ではやってみます.$\epsilon=1/q$ とします.任意の $\delta>0$ に対して $N>\displaystyle\frac{\sqrt{2}}{\delta}$ なる自然数 $N$ をとり$$x=a+\frac{\sqrt{2}}{N}$$と定めます.この $x$ は無理数ですので $f(x)=0$ です.よって$$|x-a|=\frac{\sqrt{2}}{N}<\delta \;かつ\; |f(x)-f(a)|=\frac{1}{q}\ge\epsilon$$これは不連続ということです.よってあらゆる有理数点での不連続性が示されました。
② $a$ が無理数の場合
$f(a)=0$ です.$x$ も無理数であれば $|f(x)-f(a)|=0$ となるのでこれ以上論じる必要はありません.
問題は $x$ が有理数の場合です.$\delta$ をうまくとって連続性を示せるでしょうか.簡単のため,区間 $(0,1)$ に絞って考えてみます.
$a$ の周りには有理数点がたくさんあります.しかし $a$ は無理数ですから,それらの有理数と等しくはありません.ですので $\delta$ を十分に小さくとれば $a$ の $\delta$ 近傍からそれらの有理数を排除できます.しかしすべての有理数点を排除するわけではありません(無限回の手続きが必要になってしまうので).分母の小さい有理数点から順に排除していくと,$a$ の近傍に残るのは十分に大きい分母の有理数点であり,$f(x)=1/q$ ですから $f(x)$ は $0$ に近くなります.すると $|f(x)-f(a)|=1/q$ を $\epsilon$ 未満に押さえられるのではないか,と考えるのです.
実際にやっていきましょう.
任意の $\epsilon>0$ に対して $N\epsilon>1$ なる自然数 $N$ をとると $1/N<\epsilon$ が成り立ちます.ここで
・$\delta_2=\left|a-\displaystyle\frac{1}{2}\right|$ ととると $|x-a|<\delta_2$ なる $x$ は $1/2$ を取りえません。よって$1/2$は排除できました.
・$\delta_3=\min\left\{\left|a-\displaystyle\frac{1}{3}\right|,\left|a-\displaystyle\frac{2}{3}\right|\right\}$ ととると $|x-a|<\delta_3$ なる $x$ は $1/3$ , $2/3$ を取りえません.よって$1/3$と$2/3$は排除できました.
以下くりかえし,最後に
・$\delta_N=\min\left\{\left|a-\displaystyle\frac{1}{N}\right|,\cdots,\left|a-\displaystyle\frac{N-1}{N}\right|\right\}$ ととると $|x-a|<\delta_N$ なる $x$ は $1/N$ , $2/N$ ,..., $(N-1)/N$ を取りえません.
ゆえに $\delta=\min\{\delta_2,\delta_3,\cdots,\delta_N\}$ ととれば $|x-a|<\delta$ を満たす有理数 $x$ は分母が $N$ より大きいものに限られます.従って$$|x-a|<\delta\Longrightarrow |f(x)-f(a)|=|f(x)|<\frac{1}{N}<\epsilon$$これであらゆる無理数点での連続性が示されました.
以上①②よりトマエ関数はあらゆる有理数で不連続,あらゆる無理数で連続となります.
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。