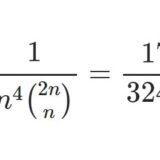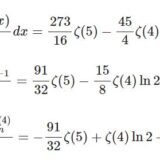前回の記事からの延長です:
$\arcsin^k x$ のマクローリン展開をおこなう。結果として二項係数や有限多重ゼータを含む規則的な形の級数が現れることを示す。
過去にすでに導出しましたが、Edwards[1] p74に載った別の方法を紹介します。$$y=f(x):=\arcsin^2x$$と定義すると$$y'=\frac{2\arcsin x}{\sqrt{1-x^2}}$$となるので$$(1-x^2)(y')^2=4y$$と書けます。再度微分すると\begin{equation}(1-x^2)y''=xy'+2\tag{1}\end{equation}これを級数法によって解きましょう。$$y=\sum_{n=0}^\infty a_nx^n$$とおいて(1)に代入すると\begin{equation}\sum_{n=0}^\infty (n+1)(n+2)a_{n+2}x^n-\sum_{n=1}^\infty (n-1)na_nx^n =2+\sum_{n=1}^\infty na_nx^n\tag{2}\end{equation}$f(0)=0$ , $f'(0)=0$ なので $a_0=0$ , $a_1=0$ です。(2)が恒等的に成り立つので\begin{equation}\begin{cases}a_{n+2} =\dfrac{n^2}{(n+1)(n+2)}a_n\quad (n\ge 1)\\ a_0=a_1=0\;,\;a_2=1\end{cases}\tag{3}\end{equation}です。したがって $a_1=a_3=a_5=\cdots=0$ であり、$$a_{2n}=\frac{2\cdot(2n-2)!!^2}{(2n)!}$$となります。少し変形して$$a_{2n}=\frac{2^{2n}}{2n^2\binom{2n}{n}}$$よって求める展開式は
$$\arcsin^2x = \frac{1}{2}\sum_{n=1}^\infty\frac{(2x)^{2n}}{n^2\binom{2n}{n}}$$
これで $k=2$ でのマクローリン展開ができました。
[1]のp77で紹介されている方法で $k=2,3,4,5,6$ を求めてみましょう。$$y=f(x):=e^{m\arcsin x}$$と定義すると$$y'=\frac{my}{\sqrt{1-x^2}}$$再度微分して\begin{align}y'' &=\frac{m}{\sqrt{1-x^2}}y'+\frac{mx}{(1-x^2)^\frac{3}{2}}y\\ &=\frac{m}{\sqrt{1-x^2}}\frac{my}{\sqrt{1-x^2}}+\frac{mx}{(1-x^2)^\frac{3}{2}}\frac{y'\sqrt{1-x^2}}{m}\\ &=\frac{m^2y+xy'}{1-x^2}\end{align}よって $y$ が満たす微分方程式は\begin{equation}(1-x^2)y''=xy'+m^2y\tag{4}\end{equation}これに級数法を適用します。$$y=\sum_{n=0}^\infty a_nx^n$$とおいて(4)に代入します。$f(0)=1$ , $f'(0)=m$ から $a_0=1$ , $a_1=m$ であることも併せて\begin{equation}\begin{cases}a_{n+2} =\dfrac{m^2+n^2}{(n+1)(n+2)}a_n\quad (n\ge 0)\\ a_0=1\;,\;a_1=m\end{cases}\tag{5}\end{equation}これは次のように書き下せます。
\begin{align}e^{m\arcsin x} &= 1+ mx +\frac{m^2}{2!}x^2 \\&\quad+ \frac{m(m^2+1)}{3!}x^3+\frac{m^2(m^2+2^2)}{4!}x^4\\&\quad +\frac{m(m^2+1)(m^2+3^2)}{5!}x^5+\frac{m^2(m^2+2^2)(m^2+4^2)}{6!}x^6+\cdots\tag{6}\end{align}
一方で $e^t$ の有名なマクローリン展開公式から$$e^{m\arcsin x}=1+m\arcsin x+\frac{m^2\arcsin^2x}{2!}+\frac{m^3\arcsin^3x}{3!}+\cdots$$ですが、$m$ で整理すると
\begin{align}e^{m\arcsin x}&= 1+m\left(x+\frac{x^3}{3!}+\frac{1^23^2}{5!}x^5+\frac{3^25^2}{7!}x^7+\cdots\right)\\ &\quad+m^2\left(\frac{x^2}{2!}+\frac{2^2}{4!}x^4+\frac{2^24^2}{6!}x^6+\frac{2^24^26^2}{8!}x^8+\cdots\right)\\ &\quad+m^3\left(\frac{x^3}{3!}+\frac{1^2+3^2}{5!}x^5+\frac{1^23^2+1^25^2+3^25^2}{7!}x^7+\frac{1^23^25^2+1^25^27^2+1^23^27^2+3^25^27^2}{9!}x^9+\cdots\right)\\ &\quad+m^4\left(\frac{x^4}{4!}+\frac{2^2+4^2}{6!}x^6+\frac{2^24^2+2^26^2+4^26^2}{8!}x^8+\frac{2^24^26^2+2^26^28^2+2^24^28^2+4^26^28^2}{10!}x^{10}+\cdots\right)\\ &\quad+m^5\left(\frac{x^5}{5!}+\frac{1^2+3^2+5^2}{7!}x^7+\frac{1^23^2+1^25^2+1^27^2+3^25^2+3^27^2+5^27^2}{9!}x^9+\cdots\right)\\ &\quad+m^6\left(\frac{x^6}{6!}+\frac{2^2+4^2+6^2}{8!}x^8+\frac{2^24^2+2^26^2+2^28^2+4^26^2+4^28^2+6^28^2}{10!}x^{10}+\cdots\right)\\&\quad\vdots\tag{7}\end{align}
(6)(7)を $m$ の次数ごとに比較していきます。まず $m$ の1次では$$\arcsin x=\sum_{n=0}^\infty\frac{(2n-1)!!^2}{(2n+1)!}x^{2n+1}$$あるいは少し整理して\begin{equation}\arcsin x=\sum_{n=0}^\infty\frac{1}{2^{2n}}\binom{2n}{n}\frac{x^{2n+1}}{2n+1}\tag{8}\end{equation}
次に $m$ の2次を比較すると定理1と同じ式を得ます。
$m$ の3次(あるいはそれ以降)は非常に見えにくい形をしていますが、Borwein & Chamberland [2] で面白い表記が示されています。$m$ の3次をとりあえずまともに書くと$$\frac{\arcsin^3x}{3!}=\frac{x^3}{3!}+\frac{1^2+3^2}{5!}x^5+\frac{1^23^2+1^25^2+3^25^2}{7!}x^7+\frac{1^23^25^2+1^25^27^2+1^23^27^2+3^25^27^2}{9!}x^9+\cdots$$ここで\begin{align}\frac{1^2+3^2}{5!} &=\frac{1^23^2}{5!}\left(1+\frac{1}{3^2}\right)\\\frac{1^23^2+1^25^2+3^25^2}{7!} &=\frac{1^23^25^2}{7!}\left(1+\frac{1}{3^2}+\frac{1}{5^2}\right)\end{align}のように書き換えれば$$\arcsin^3x=6\sum_{n=1}^\infty\frac{1}{2^{2n}}\binom{2n}{n}O_n^{(2)}\frac{x^{2n+1}}{2n+1}$$ここで $O^{(p)}_n$ は一般化された奇調和数で\begin{equation}O^{(p)}_n :=1+\frac{1}{3^p}+\frac{1}{5^p}+\cdots+\frac{1}{(2n-1)^p}\tag{9}\end{equation}
$m$ の4次でも同様にして$$\arcsin^4x=\frac{3}{2}\sum_{n=1}^\infty\frac{H_{n-1}^{(2)}}{n^2\binom{2n}{n}}(2x)^{2n}$$ここで $H^{(p)}_n$ は一般化された調和数で\begin{equation}H^{(p)}_n :=1+\frac{1}{2^p}+\frac{1}{3^p}+\cdots+\frac{1}{n^p}\tag{10}\end{equation}$H^{(p)}_0=O^{(p)}_0=0$ と定義されますので、$n=0$ を級数のスタートとしてもいいです。
$m$ の5次では$$1^2+3^2+5^2=1^23^25^2\left\{\frac{1}{3^2}+\frac{1}{5^2}\left(1+\frac{1}{3^2}\right)\right\}$$とか$$1^23^2+1^25^2+1^27^2+3^25^2+3^27^2+5^27^2=(1^23^25^27^2)\left\{\frac{1}{3^2}+\frac{1}{5^2}\left(1+\frac{1}{3^2}\right)+\frac{1}{7^2}\left(1+\frac{1}{3^2}+\frac{1}{5^2}\right)\right\}$$と書き換えられることを利用すると$$\arcsin^5x=120\sum_{n=1}^\infty\frac{1}{2^{2n}}\binom{2n}{n}\left\{\sum_{m=1}^{n-1}\sum_{k=0}^{m-1}\frac{1}{(2m+1)^2(2k+1)^2}\right\}\frac{x^{2n+1}}{2n+1}$$$n$ の和を1からにしていますが、実際は $n=1,2$ の項はゼロですので $n=3$ からの和をとることになります。中括弧の中は調和数が二重になったようにできています。汎用性を高めるために少し書き換えて$$\arcsin^5x=120\sum_{n=1}^\infty\frac{1}{2^{2n}}\binom{2n}{n}\left\{\sum_{0\le n_1<n_2<n}\frac{1}{(2n_1+1)^2(2n_2+1)^2}\right\}\frac{x^{2n+1}}{2n+1}$$
これと同様に $m$ の6次にも取り組むと$$\arcsin^6x=\frac{45}{4}\sum_{n=1}^\infty\frac{(2x)^{2n}}{n^2\binom{2n}{n}}\sum_{0<n_1<n_2<n}\frac{1}{n_1^{~2}n_2^{~2}}$$
このようにすればいくらでも次数を上げられますが、しんどいのでやめます。二重和だったところが三重、四重と増えていきます。詳細は[2]を見てください。
\begin{align}\arcsin x &=\sum_{n=0}^\infty\frac{1}{2^{2n}}\binom{2n}{n}\frac{x^{2n+1}}{2n+1}\\\arcsin^3x&=6\sum_{n=1}^\infty\frac{1}{2^{2n}}\binom{2n}{n}\left\{\sum_{0\le n_1<n}\frac{1}{(2n_1+1)^2}\right\}\frac{x^{2n+1}}{2n+1}\\\arcsin^5x&=120\sum_{n=1}^\infty\frac{1}{2^{2n}}\binom{2n}{n}\left\{\sum_{0\le n_1<n_2<n}\frac{1}{(2n_1+1)^2(2n_2+1)^2}\right\}\frac{x^{2n+1}}{2n+1}\end{align}
\begin{align}\arcsin^2x &= \frac{1}{2}\sum_{n=1}^\infty\frac{(2x)^{2n}}{n^2\binom{2n}{n}} \\\arcsin^4x &=\frac{3}{2}\sum_{n=1}^\infty\frac{(2x)^{2n}}{n^2\binom{2n}{n}}\sum_{0<n_1<n}\frac{1}{n_1^{~2}}\\\arcsin^6x&=\frac{45}{4}\sum_{n=1}^\infty\frac{(2x)^{2n}}{n^2\binom{2n}{n}}\sum_{0<n_1<n_2<n}\frac{1}{n_1^{~2}n_2^{~2}}\end{align}
$n_1,n_2,\cdots$ の和を「有限多重ゼータ」とか「多重調和和」と呼ぶようです。ツイッターで教えていただきました。
第1種スターリング数を使ってマクローリン展開を得る論文もあります[3]。参考までに。
定理3を使って、$\arcsin^kx$ を含む積分とかを検討したいです。
[1] Edwards, J(1896). Differential Calculus for Beginners. MacMillan, London, UK [2] Borwein, J.M, Chamberland, M(2007). Integer Powers of Arcsin. International Journal of Mathematics and Mathematical Sciences vol.2007 [3] Guo, Bai-Ni & Lim, Dongkyu & Qi, Feng. (2021). Maclaurin series expansions for powers of inverse (hyperbolic) sine, for powers of inverse (hyperbolic) tangent, and for incomplete gamma functions, with applications to second kind Bell polynomials and generalized logsine function. [4] B.C.Berndt, "Ramanujan’s Notebooks Part I"(1985)
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。