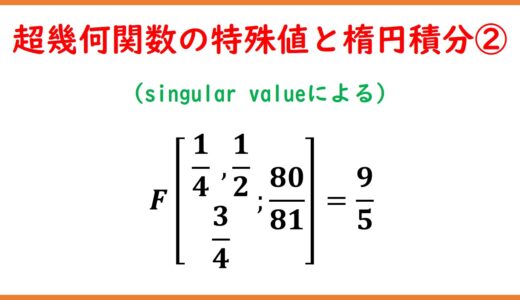
前回の記事はこちら:
超幾何関数の基礎的な知識を前提としています。超幾何関数が満たす微分方程式については
変換公式については例えば:
超幾何関数を応用した初等関数の積分は例えば:
ガンマ関数も駆使します:
$$F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};z\right)$$の値について考察する。
参考文献は、数学誌『Mathematical Proceedings of the Cambridge Philosophical Society』の109巻(1991年)に掲載されたG.S.Joyce and I.J.Zucker, Special values of the hypergeometric series. です(以下、"Joyce-Zucker(1991)")。
あと、数学誌「Annales scientifiques de l'École Normale Supérieure」の10巻(2) (1881)に掲載されたGoursat.É, "Sur l'équation différentielle linéaire, qui admet pour intégrale la série hypergéométrique."です(以下、"Goursat(1881)")。
Goursat(1881)には2F1の三次変換公式が大量に載っており、そのうちp139の(123)式\begin{equation}F\left(\begin{matrix}3a,a+\frac{1}{6}\\\frac{1}{2}\end{matrix};z\right)=\left(1+\frac{z}{3}\right)^{-3a}F\left(\begin{matrix}a,a+\frac{1}{3}\\\frac{1}{2}\end{matrix};\frac{z(z-9)^2}{(z+3)^3}\right)\tag{1.1}\end{equation}で $a=\frac{1}{12}$ とすると\begin{equation}F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};\frac{z(z-9)^2}{(z+3)^3}\right)=\left(1+\frac{z}{3}\right)^{\frac{1}{4}}F\left(\begin{matrix}\frac{1}{4},\frac{1}{4}\\\frac{1}{2}\end{matrix};z\right)\tag{1.2}\end{equation}
過去記事で証明したKummerの公式\begin{eqnarray}\frac{2\sqrt{\pi}\G(\frac{a+b+1}{2})}{\G(\frac{a+1}{2})\G(\frac{b+1}{2})}F\left(\begin{matrix}\frac{a}{2},\frac{b}{2}\\\frac{1}{2}\end{matrix};z\right)&=&F\left(\begin{matrix}a,b\\\frac{a+b+1}{2}\end{matrix};\frac{1+\sqrt{z}}{2}\right)+F\left(\begin{matrix}a,b\\\frac{a+b+1}{2}\end{matrix};\frac{1-\sqrt{z}}{2}\right)\tag{2.1}\end{eqnarray}で $a=b=\frac{1}{2}$ とします。左辺にはガンマ関数の相反公式を使うと\begin{eqnarray}\frac{\G^2(\frac{1}{4})}{\pi^\frac{3}{2}}F\left(\begin{matrix}\frac{1}{4},\frac{1}{4}\\\frac{1}{2}\end{matrix};z\right)&=&F\left(\begin{matrix}\frac{1}{2},\frac{1}{2}\\1\end{matrix};\frac{1+\sqrt{z}}{2}\right)+F\left(\begin{matrix}\frac{1}{2},\frac{1}{2}\\1\end{matrix};\frac{1-\sqrt{z}}{2}\right)\tag{2.2}\end{eqnarray}
第1種完全楕円積分 $K(k)$ は超幾何関数で次のように表されます。\begin{equation}K(k)=\frac{\pi}{2}F\left(\begin{matrix}\frac{1}{2},\frac{1}{2}\\1\end{matrix};k^2\right)\tag{3.1}\end{equation}この $k$ を母数(modulus)と呼びます。これに対し $k':=\sqrt{1-k^2}$ を補母数といいます。
いま、$k=\sqrt{\frac{1+\sqrt{z}}{2}}$ とすると $k'=\sqrt{\frac{1-\sqrt{z}}{2}}$ となりますので(2.2)に用いると\begin{eqnarray}\frac{\G^2(\frac{1}{4})}{\pi^\frac{3}{2}}F\left(\begin{matrix}\frac{1}{4},\frac{1}{4}\\\frac{1}{2}\end{matrix};z\right)&=&\frac{2}{\pi}K(k)+\frac{2}{\pi}K(k')\tag{3.2}\end{eqnarray}\begin{eqnarray}\therefore\quad\frac{\G^2(\frac{1}{4})}{2\sqrt{\pi}}F\left(\begin{matrix}\frac{1}{4},\frac{1}{4}\\\frac{1}{2}\end{matrix};z\right)&=&K(k)+K(k')\tag{3.3}\end{eqnarray}この $K(k')$ は $k$ の関数として $K'(k)$ と書くこともあります、これを「補完全楕円積分」といいます。$'$ は微分とは無関係です。
(1.2)と合わせましょう。$z=1-4(kk')^2$ であることに注意します。\begin{equation}F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};\frac{z(z-9)^2}{(z+3)^3}\right)=\frac{2\sqrt{2\pi}}{3^\frac{1}{4}\G^2(\frac{1}{4})}\left(1-k^2k'^2\right)^{\frac{1}{4}}\left(K(k)+K'(k)\right)\tag{3.4}\end{equation}左辺の $z$ も $k$ , $k'$ に置き換えます。\begin{equation}\frac{z(z-9)^2}{(z+3)^3}=\frac{\left[1-4(kk')^2\right]\left[2+(kk')^2\right]^2}{4\left[1-(kk')^2\right]^3}:=\xi(k)\tag{3.5}\end{equation}というわけで以下のように書けます。
\begin{equation}F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};\xi(k)\right)=\frac{2\sqrt{2\pi}}{3^\frac{1}{4}\G^2(\frac{1}{4})}\left(1-k^2k'^2\right)^{\frac{1}{4}}\left(K(k)+K'(k)\right)\tag{3.6}\end{equation}ただし$$\xi(k)=\frac{\left[1-4(kk')^2\right]\left[2+(kk')^2\right]^2}{4\left[1-(kk')^2\right]^3}$$
$k$ に適切な値を代入することで好きな $\xi$ をある程度見つけることができるので、$F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};z\right)$ の一般的な値をほぼ公式化できたことになります。
ここから先は、右辺の楕円積分をガンマ関数や代数的な式で表せる特殊値を考えていきましょう。
定理1の右辺を $K(k)$ でくくると\begin{equation}F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};\xi(k)\right)=\frac{2\sqrt{2\pi}}{3^\frac{1}{4}\G^2(\frac{1}{4})}\left(1-k^2k'^2\right)^{\frac{1}{4}}K(k)\left(1+\frac{K'}{K}(k)\right)\tag{4.1}\end{equation}楕円積分の値としては $k=\frac{1}{\sqrt{2}}$ がよく知られています。このとき $k'=\frac{1}{\sqrt{2}}$ です。過去記事の「2022/10/5B」で求めたように$$K\left(\frac{1}{\sqrt{2}}\right)=\frac{\G^2(\frac{1}{4})}{4\sqrt{\pi}}$$となります。いまは $K=K'$ なので $\frac{K'}{K}=1$ です。よって(4.1)を計算できますが、$\xi=0$ になってしまうので $1=1$ という無意味な式ができあがります。
$k_1=\frac{1}{\sqrt{2}}$ はダメでしたが、ほかの値はどうでしょう。$k_2=\sqrt{2}-1$ とすると $k'_2=\sqrt{2}\sqrt{\sqrt{2}-1}$ です。楕円積分に関する公式\begin{equation}K(k)=\frac{1}{1+k}K\left(\frac{2\sqrt{k}}{1+k}\right)\tag{4.2}\end{equation}によって $\frac{K'}{K}(k_2)=\sqrt{2}$ を導くことができます。さらに\begin{equation}K(k_2)=\frac{\sqrt{\sqrt{2}+1}\G(\frac{1}{8})\G(\frac{3}{8})}{2^\frac{13}{4}\sqrt{\pi}}\tag{4.3}\end{equation}を使うことで\begin{equation}F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};\frac{98}{125}\right)=\left(\frac{5}{384}\right)^\frac{1}{4}(\sqrt{2}+1)\frac{\G(\frac{1}{8})\G(\frac{3}{8})}{\G^2(\frac{1}{4})}\tag{4.4}\end{equation}※しんどいのでMaxima等で計算しましょう!
楕円積分の理論によるとsingular valuesとよばれる値 $k=k_N$ をとると、楕円積分はガンマ関数や代数的な数で表され、なんと $\frac{K'}{K}(k_N)=\sqrt{N}$ となります。例えば\begin{eqnarray*}k_1 &=&\frac{1}{\sqrt{2}}\\ k_2 &=& \sqrt{2}-1 \\ k_3&=& \frac{\sqrt{3}-1}{2\sqrt{2}}\\ k_4 &=& 3-2\sqrt{2}\end{eqnarray*}Joyce-Zucker(1991)には $N=25$ あたりまで、値がきれいになるものを書いてありますので、よかったら読んでみてください。あるいは"elliptic function , singular value"等で検索してもいいでしょう。
特に $N=4$ は$$K(k_4)=\frac{\sqrt{2}+1}{8\sqrt{2\pi}}\G^2\left(\frac{1}{4}\right)$$であり\begin{equation}F\left(\begin{matrix}\frac{1}{12},\frac{5}{12}\\\frac{1}{2}\end{matrix};\frac{1323}{1331}\right)=\frac{3}{4}11^\frac{1}{4}\tag{4.5}\end{equation}という驚異的に美しい式になります。
次回はこちら:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。