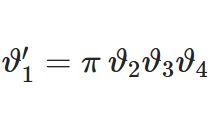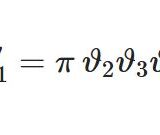前回は:
\begin{equation}f(z):=\prod_{n=1}^\infty\left(1-q^{2n-1}e^{2\pi iz}\right)\prod_{n=1}^\infty\left(1-q^{2n-1}e^{-2\pi iz}\right)\tag{1}\end{equation}なる $f$ を定義します。これまでと同様 $q:=e^{\pi i\tau}$ , $\Im\tau>0$ であることに留意します。すると\begin{equation}|q|=e^{-\pi \Im\tau}<1\tag{2}\end{equation}なる関係が容易に導かれます。
さて無限積で定義された $f(z)$ はいかなる関数でしょう。まず無限積の収束性を調べます。\begin{align}\sum_{n=1}^\infty\left|q^{2n-1}e^{\pm 2\pi i z}\right| &= \sum_{n=1}^\infty |q|^{2n-1}e^{\mp 2\pi \Im z}\\ &= e^{\mp 2\pi \Im z}\sum_{n=1}^\infty e^{-(2n-1)\pi \Im\tau}\end{align}$|z|\le R$ においては $|\Im z|\le R$ であり、(2)も用いて$$\le e^{2\pi R}\sum_{n=1}^\infty e^{-(2n-1)\pi \Im\tau} <+\infty$$よって$$\sum_{n=1}^\infty\left|q^{2n-1}e^{\pm 2\pi i z}\right|$$は $\CC$ 上で広義一様収束します。
よってこちらの定理6.8より2つの無限積$$\prod_{n=1}^\infty\left(1-q^{2n-1}e^{2\pi iz}\right)\;,\quad\prod_{n=1}^\infty\left(1-q^{2n-1}e^{-2\pi iz}\right)$$はともに広義絶対一様収束して、収束先の関数は $\CC$ 上で解析的です。よって $f(z)$ は整関数です。
$f(z)$ の零点を調べます。無限積の因数のうち1つでもゼロとなるものがあれば $f(z)=0$ となることを踏まえて、零点となる $z$ が満たす条件は$$e^{\pi i\tau(2n-1)}e^{\pm 2\pi iz}=1$$なので$$\pi i\tau(2n-1)\pm 2\pi iz=2\pi i N\quad (N\in\ZZ)$$と書ければよいことになります。$z$ について解くと$$z=N\pm \left(n-\frac{1}{2}\right)\tau$$が零点です。$N$ は全整数、$n$ は全自然数ですので $f(z)$ の零点はテータ関数 $\vartheta_4(z)$ の零点と一致します。
ここで現れた零点はすべて1位ですので$$\frac{\vartheta_4(z)}{f(z)}$$は極も零点ももちません。また(1)から$$f(z+1)=f(z)$$がすぐに分かり、$$f(z+\tau)=-q^{-1}e^{-2\pi iz}f(z)$$も少々の計算で導けます。テータ関数の擬周期性$$\vartheta_4(z+1)=\vartheta_4(z)\;,\; \vartheta_4(z+\tau)=-q^{-1}e^{-2\pi iz}\vartheta_4(z)$$より $\frac{\vartheta_4(z)}{f(z)}$ は二重周期関数です。極をもたない二重周期関数は定数に限るので、定数 $C$ を用いて\begin{equation}\vartheta_4(z)=C\prod_{n=1}^\infty\left(1-q^{2n-1}e^{2\pi iz}\right)\prod_{n=1}^\infty\left(1-q^{2n-1}e^{-2\pi iz}\right)\tag{3}\end{equation}あるいは\begin{equation}\vartheta_4(z)=C\prod_{n=1}^\infty\left(1-2q^{2n-1}\cos 2\pi z+q^{4n-2}\right)\tag{4}\end{equation}なお定数 $C$ は\begin{equation}C=\prod_{n=1}^\infty (1-q^{2n})\tag{5}\end{equation}です。(5)は次回以降の記事で示す予定です。
ヤコビの三重積を使って(5)を求めることもできます。
ここから残りの $\vartheta_1$ , $\vartheta_2$ , $\vartheta_3$ を計算しましょう。こちらを参考にして変換します。(3)あるいは(4)の $z$ に $z+\frac{1}{2}$ を代入して\begin{equation}\vartheta_3(z)=C\prod_{n=1}^\infty\left(1+q^{2n-1}e^{2\pi iz}\right)\prod_{n=1}^\infty\left(1+q^{2n-1}e^{-2\pi iz}\right)\tag{6}\end{equation}あるいは\begin{equation}\vartheta_3(z)=C\prod_{n=1}^\infty\left(1+2q^{2n-1}\cos 2\pi z+q^{4n-2}\right)\tag{7}\end{equation}を得ます。
また$$\vartheta_1(z) =-iq^{1/4}e^{\pi iz}\vartheta_4\left(z+\frac{\tau}{2}\right)$$に(3)あるいは(4)を用いて\begin{equation}\vartheta_1(z)=2Cq^{1/4}\sin\pi z\prod_{n=1}^\infty\left(1-q^{2n}e^{2\pi iz}\right)\prod_{n=1}^\infty\left(1-q^{2n}e^{-2\pi iz}\right)\tag{8}\end{equation}と\begin{equation}\vartheta_1(z)=2Cq^{1/4}\sin\pi z\prod_{n=1}^\infty\left(1-2q^{2n}\cos 2\pi z+q^{4n}\right)\tag{9}\end{equation}を得ます。
最後に $\vartheta_2(z)=\vartheta_1(z+\frac{1}{2})$ より(8)(9)を使って\begin{equation}\vartheta_2(z)=2Cq^{1/4}\cos\pi z\prod_{n=1}^\infty\left(1+q^{2n}e^{2\pi iz}\right)\prod_{n=1}^\infty\left(1+q^{2n}e^{-2\pi iz}\right)\tag{10}\end{equation}と\begin{equation}\vartheta_2(z)=2Cq^{1/4}\cos\pi z\prod_{n=1}^\infty\left(1+2q^{2n}\cos 2\pi z+q^{4n}\right)\tag{11}\end{equation}を得ます。
以上をまとめて
\begin{align}\vartheta_1(z)&=2Cq^{1/4}\sin\pi z\prod_{n=1}^\infty\left(1-2q^{2n}\cos 2\pi z+q^{4n}\right)\\\vartheta_2(z)&=2Cq^{1/4}\cos\pi z\prod_{n=1}^\infty\left(1+2q^{2n}\cos 2\pi z+q^{4n}\right)\\\vartheta_3(z)&=C\prod_{n=1}^\infty\left(1+2q^{2n-1}\cos 2\pi z+q^{4n-2}\right)\\\vartheta_4(z)&=C\prod_{n=1}^\infty\left(1-2q^{2n-1}\cos 2\pi z+q^{4n-2}\right)\end{align}ただし$$C=\prod_{n=1}^\infty (1-q^{2n})$$
定理1で $z=0$ とおくことで次を得ます:
\begin{align}\vartheta_1(0)&=0\\\vartheta_2(0)&=2Cq^{1/4}\left[\prod_{n=1}^\infty\left(1+q^{2n}\right)\right]^2\\\vartheta_3(0)&=C\left[\prod_{n=1}^\infty\left(1+q^{2n-1}\right)\right]^2\\\vartheta_4(0)&=C\left[\prod_{n=1}^\infty\left(1-q^{2n-1}\right)\right]^2\end{align}ただし$$C=\prod_{n=1}^\infty (1-q^{2n})$$
以下、テータ定数は $\vartheta_i:=\vartheta_i(0)$ と書くことにします。
こちらの系4より$$\vartheta_2^{~4}+\vartheta_4^{~4}=\vartheta_3^{~4}$$なので
$$16q\left[\prod_{n=1}^\infty\left(1+q^{2n}\right)\right]^8+\left[\prod_{n=1}^\infty\left(1-q^{2n-1}\right)\right]^8=\left[\prod_{n=1}^\infty\left(1+q^{2n-1}\right)\right]^8$$
無限積の表現のしかたの1つとしてq-ポッホハマー記号というものがあります。\begin{equation}(a;q)_\infty :=\prod_{n=0}^\infty(1-aq^n)\tag{12}\end{equation}$n=0$ からスタートしていることに気をつけると、例えば系2に出てくる積は\begin{align}\prod_{n=1}^\infty\left(1+q^{2n}\right) &= (-q^2;q^2)_\infty\\\prod_{n=1}^\infty\left(1+q^{2n-1}\right) &= (-q;q^2)_\infty\\\prod_{n=1}^\infty\left(1-q^{2n-1}\right) &= (q;q^2)_\infty\end{align}
少し短いですが、きりがいいので今日はここまで。
第5版です。いわずと知れた名著。楕円関数にかなりのページを割いています。

Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。