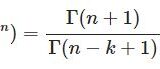三角関数が含まれる定積分はたくさんありますが、コサインの平方根 $\sqrt{\cos x}$ について考察してみたいと思います。
$$I=\displaystyle\int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx$$はいかなる値か.
あとで分かるように初等的には解けませんがWolframにやらせてみたら面白い答えが出ました。ただその答えをどのように導出するかが分からなかったので頑張ってみました。私のたどった過程を問題形式にして示していきますので、読んでみてください。ちなみにこの過程はやや邪魔くさいので、さっさと結論へたどり着くには本記事の終盤「問EX」⇒「問5」のベータ関数の部分⇒「問6」を読めばOKです。
この定積分は$$I = \int_0^{\frac{\pi}{2}}(1-\sin^2 x)^\frac{1}{4}dx$$と変形できます。そこで次の一手は級数表示です。
$(1-x)^\frac{1}{4}$ を $x=0$ のまわりにテイラー展開し、$$(1-x)^\frac{1}{4}=1+\sum^\infty_{n=1}\left[\left(-\frac{1}{4}\right)\frac{3}{4}\frac{7}{4}\cdots\frac{4n-5}{4}\cdot\frac{x^n}{n!}\right]$$を導け.
次々と微分していけば大丈夫です。この結果はガンマ関数を使って、$$(1-x)^\frac{1}{4}=\sum^\infty_{n=0}\frac{\Gamma(n-\frac{1}{4})}{\Gamma(-\frac{1}{4})}\cdot \frac{x^n}{n!}$$とも書けます。
上記の結果より$$\int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx=\sum^\infty_{n=0}\frac{\Gamma(n-\frac{1}{4})}{\Gamma(-\frac{1}{4})}\cdot \frac{1}{n!}\int_0^{\frac{\pi}{2}}\sin^{2n}xdx$$であることを確認せよ.
問1の $x$ を $\sin^2x$ に置き換えるだけですね。ここから $\sin^{2n}$ の積分を計算しないといけません。
$\displaystyle\int_0^{\frac{\pi}{2}}\sin^{2n}xdx$ を計算せよ.
高等学校の数学にも頻出しますね。部分積分すると漸化式が現れるので、それを解くことで$$\int_0^{\frac{\pi}{2}}\sin^{2n}xdx=\frac{(2n-1)!!}{(2n)!!}\cdot\frac{\pi}{2}$$を得ます。
従って求める積分 $I$ は$$I=\frac{\pi}{2}\sum^\infty_{n=0}\frac{\Gamma(n-\frac{1}{4})}{\Gamma(-\frac{1}{4})}\cdot \frac{1}{n!}\cdot \frac{(2n-1)!!}{(2n)!!}$$となるわけです。ここからどうするべきか長考しましたが、少し前に知った「超幾何級数」の形でとりあえず書けないかなぁと思い、以下の方法で取り組みました。
ポッホハマー記号$$(a)_n=a(a+1)(a+2)\cdots(a+n-1)$$を使って$$I=\frac{\pi}{2}\sum^\infty_{n=0}\frac{(\frac{1}{2})_n(-\frac{1}{4})_n}{(1)_n}\cdot\frac{1}{n!}$$と表せることを確認せよ.
先にガンマ関数や階乗を書き下して$$I=\frac{\pi}{2}\sum^\infty_{n=0}\frac{(n-\frac{1}{2})(n-\frac{3}{2})\cdots \frac{3}{2}\cdot\frac{1}{2}}{n!n!}\cdot\left(n-\frac{5}{4}\right)\left(n-\frac{9}{4}\right)\cdots\frac{7}{4}\cdot\frac{3}{4}\cdot\frac{-1}{4}$$とあらわしておくと分かりやすいと思います。
ここでガウスの超幾何級数を導入します。$$F(a,b,c;x)\equiv\sum^\infty_{n=0}\frac{(a)_n(b)_n}{(c)_n}\cdot\frac{x^n}{n!}$$問4と比べると$$I=\frac{\pi}{2}F\left(\frac{1}{2},-\frac{1}{4},1;1\right)$$と書けることが分かります。何かまどろっこしいことしてる感じがしますね…
超幾何級数に関するオイラーの積分表示$$F(a,b,c;x)=\frac{\Gamma(c)}{\Gamma(a)\Gamma(c-a)}\int^1_0t^{a-1}(1-t)^{c-a-1}(1-tx)^{-b}dt$$を用いて,$$I=\frac{1}{2}\int_0^1 t^{-\frac{1}{2}}(1-t)^{-\frac{1}{4}}dt$$と書き直せることを示せ.さらにベータ関数によって,$$I=\frac{1}{2}B\left(\frac{1}{2},\frac{3}{4}\right)=\frac{\sqrt{\pi}}{2}\frac{\Gamma(\frac{3}{4})}{\Gamma(\frac{5}{4})}$$であることを確認せよ.
そのまま当てはめれば大丈夫と思います。最後の等号は、ベータ関数とガンマ関数の関係および $\Gamma(1/2)=\sqrt{\pi}$ によって導けます。
ガンマ関数の相反公式$$\Gamma(x)\Gamma(1-x)=\frac{\pi}{\sin \pi x}$$を用いて$$\Gamma\left(\frac{5}{4}\right)=\frac{\pi}{2\sqrt{2}}\Gamma\left(\frac{3}{4}\right)$$であることを示せ.これにより最終的な式$$I=\int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx=\sqrt{\frac{2}{\pi}}\Gamma\left(\frac{3}{4}\right)^2$$を導け.
ガンマ関数が残ってしまいますが、これでおしまいです。数値計算すると $I\approx 1.198$ となります。
というわけで積分値が求まりました(ガンマ関数を使っているのでそうとも言えませんが)。長い道のりでしたが、いろんな数学の知識を使えたのでいい勉強になったと思います。
最初からベータ関数をうまく使うことでもっと早く解けることが分かりました。これまでの長い過程はベータ関数の知識が貧弱だったからゆえであり情けないです。
冒頭の積分において $\sin^2x=t$ と変換することで$$I=\int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx=\frac{1}{2}\int_0^1 t^{-\frac{1}{2}}(1-t)^{-\frac{1}{4}}dt$$と書き直せることを示せ.
これはベータ関数です。つまりテイラー展開や超幾何級数を経ることなく問5の途中までショートカットできます.
$$ \int_0^{\frac{\pi}{2}}\sqrt{\cos x}dx=\sqrt{\frac{2}{\pi}}\Gamma\left(\frac{3}{4}\right)^2 $$
今回はコサインの平方根の定積分を扱いました。ベータ関数が現れることには驚きましたが、ベータ関数の定義である$$B(x,y)=\int^1_0t^{x-1}(1-t)^{y-1}dt$$において $t=\sin^2\theta$ と置換すると$$B(x,y)=2\int_0^{\frac{\pi}{2}}\sin^{2x-1}\theta \cos^{2y-1}\theta d\theta$$を得ます。今回の場合だとこの式に $x=\frac{1}{2} , y=\frac{3}{4}$ を代入すればいいですね。この公式があれば$\sqrt{\sin x}$ や $\sqrt{\tan x}$ さらには $\cos$ の $n$ 乗根などにも応用できますのでまた書いていこうと思います。
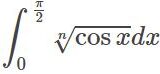 $\int\sqrt[n]{\cos x}dx$ の計算 (ガンマ関数,ベータ関数)
$\int\sqrt[n]{\cos x}dx$ の計算 (ガンマ関数,ベータ関数)
$\tan$ の $n$ 乗根でもやってみました!
 $\int\sqrt[n]{\tan x}dx$ とベータ関数
$\int\sqrt[n]{\tan x}dx$ とベータ関数
発展的な内容:
Please support me!

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。
ご支援いただいた方は、こちらで確認できます。
◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です(あっとは@に置き換えてください)。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。
◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。
OFUSEで応援を送る◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。