複素積分演習（対数と２つの分岐点）

この書籍はたくさん積分が載っていて面白いのですが、証明が書かれていないため、挑戦しました。

書籍はAmazon等で買えます。700ページもあり、非常に多くの微分・積分・級数公式が網羅されています。眺めるだけでも面白いです。

Handbook of Special Functions: Derivatives, Integrals, Series and Other Formulas

積分を２つに分ける

$I$ を計算する方針や積分経路については @_mi9ru さんに教えていただきました。ありがとうございます。

まずは $\ln(1-z)$ に着目し次の変形を行います。$$\int_0^1\frac{\sqrt{x}\ln(1-x)}{1+x^3}dx=\int_0^1\frac{\sqrt{x}\ln x}{1+x^3}dx+\int_0^1\frac{\sqrt{x}}{1+x^3}\ln\frac{1-x}{x}dx$$右辺第1項は冒頭の $I_1$、第2項は $I_2$ です。よって $I=I_1+I_2$ です。

級数による計算とカタラン定数

$I_1$ を計算します。$(1+x^3)^{-1}$ を級数展開して部分積分を行います。\begin{eqnarray*}I_1 &=& \int_0^1\frac{\sqrt{x}\ln x}{1+x^3}dx \\ &=& \sum_{n=0}^\infty (-1)^n\int_0^1 x^{3n+\frac{1}{2}}\ln xdx \\ &=& -\sum_{n=0}^\infty\frac{(-1)^n}{(3n+\frac{3}{2})^2} \\ &=& -\frac{4}{9}\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2} \\&=& -\frac{4}{9}G\end{eqnarray*}ここで $G$ はカタラン定数です。

複素積分による計算

$I_2$ の定義式において $x$ を $\dfrac{1}{x}$ と置換します。\begin{equation}I_2:=\int_0^1\frac{\sqrt{x}}{1+x^3}\ln\frac{1-x}{x}dx=\int_1^\infty\frac{\sqrt{x}\ln (x-1)}{1+x^3}dx\tag{2}\end{equation}

さて、ここで次の周回積分を考えます。$$\oint_C\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz$$経路は下図です。

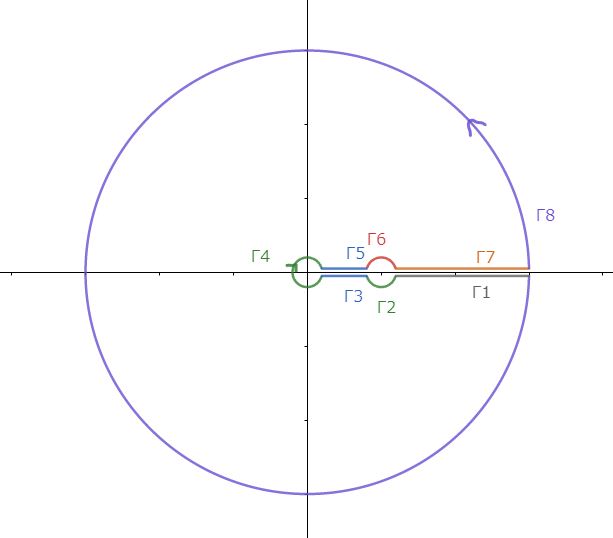
分岐点（branch point）は $0$ , $1$ , $\infty$ であることから実軸の正部分に切断を入れておきます。すると $0<\arg z<2\pi$ となり、$\ln(1-z)$ の計算には $-\pi<\arg(1-z)<\pi$ に注意するとよいです。

経路 $C$ は $\G_1$ から $\G_8$ に分けられます。このうち小円弧である $\G_2$ , $\G_4$ , $\G_6$ および大円弧 $\G_8$ の積分値は（実際に評価してみると）ゼロとなります。したがって\begin{equation}\oint_C\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz = \left(\int_{\G_1}+\int_{\G_3}+\int_{\G_5}+\int_{\G_7}\right)\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz \tag{3}\end{equation}

複素積分の変形

偏角に注意して計算をしていきます。$\G_1$ では $\arg z=2\pi$ , $\arg(1-z)=\pi$ です。$z=xe^{2\pi i}$ とすると $x$ は $\infty$ から $1$ まで変化し、$1-z=(x-1)e^{\pi i}$ となります。従って$$\int_{\G_1}\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz=\int_\infty^1\frac{\sqrt{x}e^{\pi i}\left(\ln(x-1)+\pi i\right)}{1+x^3}dx$$\begin{equation}\therefore\quad\int_{\G_1}\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz=\int_1^\infty\frac{\sqrt{x}\ln(x-1)}{1+x^3}dx+\pi i\int_1^\infty\frac{\sqrt{x}}{1+x^3}dx\tag{4}\end{equation}次に $\G_3$ では $\arg z=2\pi$ , $\arg(1-z)=0$ です。$z=xe^{2\pi i}$ , $1-z=1-x$ と置換して\begin{equation}\int_{\G_3}\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz=\int_0^1\frac{\sqrt{x}\ln(1-x)}{1+x^3}dx\tag{5}\end{equation}$\G_5$ では $\arg z=0$ , $\arg(1-z)=0$ です。$z=x$ , $1-z=1-x$ と置換して\begin{equation}\int_{\G_5}\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz=\int_0^1\frac{\sqrt{x}\ln(1-x)}{1+x^3}dx\tag{6}\end{equation}最後に $\G_7$ では $\arg z=0$ , $\arg(1-z)=-\pi$ ですので、 $z=x$ , $1-z=(x-1)e^{-\pi i}$ と置換すると $x$ は $1$ から $\infty$ まで変化します。よって\begin{equation}\therefore\quad\int_{\G_7}\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz=\int_1^\infty\frac{\sqrt{x}\ln(x-1)}{1+x^3}dx-\pi i\int_1^\infty\frac{\sqrt{x}}{1+x^3}dx\tag{7}\end{equation}(4)(5)(6)(7)を足すと(3)になるので$$\oint_C\frac{z^\frac{1}{2}\ln(1-z)}{1+z^3}dz = 2\int_0^1\frac{\sqrt{x}\ln(1-x)}{1+x^3}dx+2\int_1^\infty\frac{\sqrt{x}\ln(x-1)}{1+x^3}dx$$右辺第1項は $I$ の定義そのもの、第2項は(2)より $I_2$ に等しいです。すなわち次の式が成立します。

留数定理

あとは(8)の左辺を留数により求めましょう。$0<\arg z<2\pi$ に注意して、被積分関数は$$f(z)=\frac{z^\frac{1}{2}\ln(1-z)}{(z+1)(z-e^{\frac{\pi}{3}i})(z-e^{\frac{5\pi}{3}i})}$$と書き直せます。つまり $f(z)$ は $z=-1$ , $e^{\frac{\pi}{3}i}$ , $e^{\frac{5\pi}{3}i}$ に1位の極を持ちます。したがって\begin{eqnarray*}\mathrm{Res}_{z=-1}f(z) &=& \left.\frac{z^\frac{1}{2}\ln(1-z)}{(z-e^{\frac{\pi}{3}i})(z-e^{\frac{5\pi}{3}i})}\right|_{z=-1} \\ &=& \frac{\ln2}{3}i \\ \mathrm{Res}_{z=e^{\frac{\pi}{3}i}}f(z) &=& \left.\frac{z^\frac{1}{2}\ln(1-z)}{(z+1)(z-e^{\frac{5\pi}{3}i})}\right|_{z=e^{\frac{\pi}{3}i}} \\ &=& -\frac{\pi}{9} \\ \mathrm{Res}_{z=e^{\frac{5\pi}{3}i}}f(z) &=& \left.\frac{z^\frac{1}{2}\ln(1-z)}{(z+1)(z-e^{\frac{\pi}{3}i})}\right|_{z=e^{\frac{5\pi}{3}i}} \\ &=& \frac{\pi}{9}\end{eqnarray*}以上より

(8)(9)より$$I+I_2=-\frac{\pi}{3}\ln2$$$I=I_1+I_2$ であり、$I_1$ は(1)で求まっています。したがって\begin{equation}I_2=\frac{2}{9}G-\frac{\pi}{6}\ln2\tag{10}\end{equation}および

これで本稿の目的は達せられました。

級数展開による手法

$I$ を級数展開すると$$I=\sum_{n=0}^\infty(-1)^n\int_0^1x^{3n+\frac{1}{2}}\ln(1-x)dx$$これはベータ関数の偏微分$$\dd{B}{q}(p,q)=\int_0^1 x^{p-1}(1-x)^{q-1}\ln(1-x)dx=B(p,q)\left[\psi(q)-\psi(p+q)\right]$$を利用することで$$I=\sum_{n=0}^\infty(-1)^nB\left(3n+\frac{3}{2},1\right)\left[\psi(1)-\psi\left(3n+\frac{5}{2}\right)\right]$$と書けます。ベータ関数の偏微分については例えばこちら：

∫logsin xdx 対数正弦積分その1

計算を進めると\begin{eqnarray*}I &=& \sum_{n=0}^\infty(-1)^n\frac{1}{3n+\frac{3}{2}}\left[\psi(1)-\psi\left(3n+\frac{5}{2}\right)\right] \\ &=& \frac{1}{3n+\frac{3}{2}}\left[\psi(1)-\frac{1}{3n+\frac{3}{2}}-\frac{1}{3n+\frac{1}{2}}-\cdots -\frac{1}{\frac{1}{2}}-\psi\left(\frac{1}{2}\right)\right]\end{eqnarray*}

【γ8】ディガンマ関数の特殊値と極

で得たディガンマ関数の特殊値 $\psi(1)=-\g$ , $\psi(1/2)=-\g-2\ln2$ を代入して$$I=\frac{4}{3}\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}\left(\ln2-\sum_{k=1}^{3n+2}\frac{1}{2k-1} \right)$$第1項は\begin{equation}\sum_{n=0}^\infty\frac{(-1)^n}{2n+1}=\frac{\pi}{4}\tag{12}\end{equation}により計算できます。ここで奇調和数 $O_n$ を$$O_n:=1+\frac{1}{3}+\cdots+\frac{1}{2n-1}$$で定義すると

(13)右辺の級数が計算できれば $I$ が求まります。実は過去記事

調和数を含んだ級数(Euler-sum)とゼータ関数 part8

の(31)式が計算できればこれを計算できるのですが、(31)が求まらなかったのです。よってここから先は進むことができませんでした。残念。

ある二重対数関数の公式

(13)の方法では求まらなかったものの、別の道筋で(11)が導出できたので、逆算してとある公式を示したいと思います。(11)(13)より\begin{equation}\sum_{n=0}^\infty\frac{(-1)^nO_{3n+2}}{2n+1}=\frac{G}{6}+\frac{3}{8}\pi\ln2\tag{14}\end{equation}ここで $O_{3n}=O_{3n+2}-\frac{1}{6n+3}-\frac{1}{6n+1}$ であることを用いて\begin{eqnarray*}\sum_{n=0}^\infty\frac{(-1)^nO_{3n}}{2n+1} &=& \sum_{n=0}^\infty\frac{(-1)^nO_{3n+2}}{2n+1}-\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)(6n+3)}-\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)(6n+1)} \\ &=& \sum_{n=0}^\infty\frac{(-1)^nO_{3n+2}}{2n+1}-\frac{1}{3}\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)^2}+\frac{1}{2}\sum_{n=0}^\infty\frac{(-1)^n}{(2n+1)}-\frac{3}{2}\sum_{n=0}^\infty\frac{(-1)^n}{6n+1} \\ &=& \sum_{n=0}^\infty\frac{(-1)^nO_{3n+2}}{2n+1}-\frac{G}{3}+\frac{\pi}{8}-\frac{3}{2}\left(\frac{\pi}{6}+\frac{\ln(\sqrt{3}+1)}{\sqrt{3}}-\frac{\ln2}{2\sqrt{3}}\right) \\ &=& \sum_{n=0}^\infty\frac{(-1)^nO_{3n+2}}{2n+1}-\frac{G}{3}-\frac{\pi}{8}-\frac{\sqrt{3}}{2}\ln(\sqrt{3}+1)+\frac{\sqrt{3}}{4}\ln2\end{eqnarray*}(14)を使えば

さて、先ほどの過去記事から\begin{eqnarray}\sum_{n=1}^\infty\frac{(-1)^nO_{3n}}{2n+1} &=& \frac{G}{2}-\frac{\pi}{8} -\frac{\sqrt{3}}{2}\ln(\sqrt{3}+1)+\frac{\pi}{6}\ln(\sqrt{3}+1)\\&& +\frac{\sqrt{3}}{4}\ln2+\frac{\pi}{24}\ln2\\&&+\frac{1}{2}\mathfrak{I}\left[\Li_2\left(\frac{\sqrt{6}-\sqrt{2}}{4}e^{-\frac{5}{12}\pi i}\right)-\Li_2\left(\frac{\sqrt{6}+\sqrt{2}}{4}e^{\frac{1}{12}\pi i}\right)\right]\tag{16}\end{eqnarray}(15)(16)を合わせると

なる公式が得られます。わりと簡潔な式なので、左辺を直接計算して右辺を導けるのかもしれません。

一般化について

$$I(p)=\int_0^1\frac{x^{p-\frac{1}{2}}\ln(1-x)}{1+x^{2p+1}}dx\quad (p\in\NN)$$として先ほど議論した積分を一般化できます。$$I(p)=\int_0^1\frac{x^{p-\frac{1}{2}}\ln x}{1+x^{2p+1}}dx+\int_0^1\frac{x^{p-\frac{1}{2}}}{1+x^{2p+1}}\ln\frac{1-x}{x}dx$$とすると第1項は$$\int_0^1\frac{x^{p-\frac{1}{2}}\ln x}{1+x^{2p+1}}dx=-\frac{4G}{(2p+1)^2}$$あとは同様の複素積分により求められます。

次回の積分：

2022年9月13日 logを含む難しい積分（調和数の4倍添え字を応用）

応援のおねがい

Please support me!

まめしば

記事を気に入って下さった方、「応援してあげてもいいよ」という方がいらっしゃったら15円から可能なので支援していただければ幸いです。情報発信を継続していくため、サーバー維持費などに充てさせていただきます。

ご支援いただいた方は、こちらで確認できます。

◎ Amazonギフトの場合、
Amazonギフト券- Eメールタイプ – Amazonベーシック
より、金額は空白欄に適当に(15円から)書きこんで下さい。受取人は「mamekebiamazonあっとgmail.com」です（あっとは@に置き換えてください）。贈り主は「匿名」等でOKです。全額がクリエイターに届きます。

◎ OFUSEは登録不要で、100円から寄付できます。金額の90%がクリエイターに届きます。

OFUSEで応援を送る

◎ codocは登録不要で、100円から寄付できます。金額の85%がクリエイターに届きます。